implicate order 13

Wholeness and the Implicate Order

The Crystallization Process and the Implicate Order
(Part Thirteen)

We continue our investigation concerning the generation of group elements of the Plane Group P3m1.

The Plane Group P3m1 (Sequel)

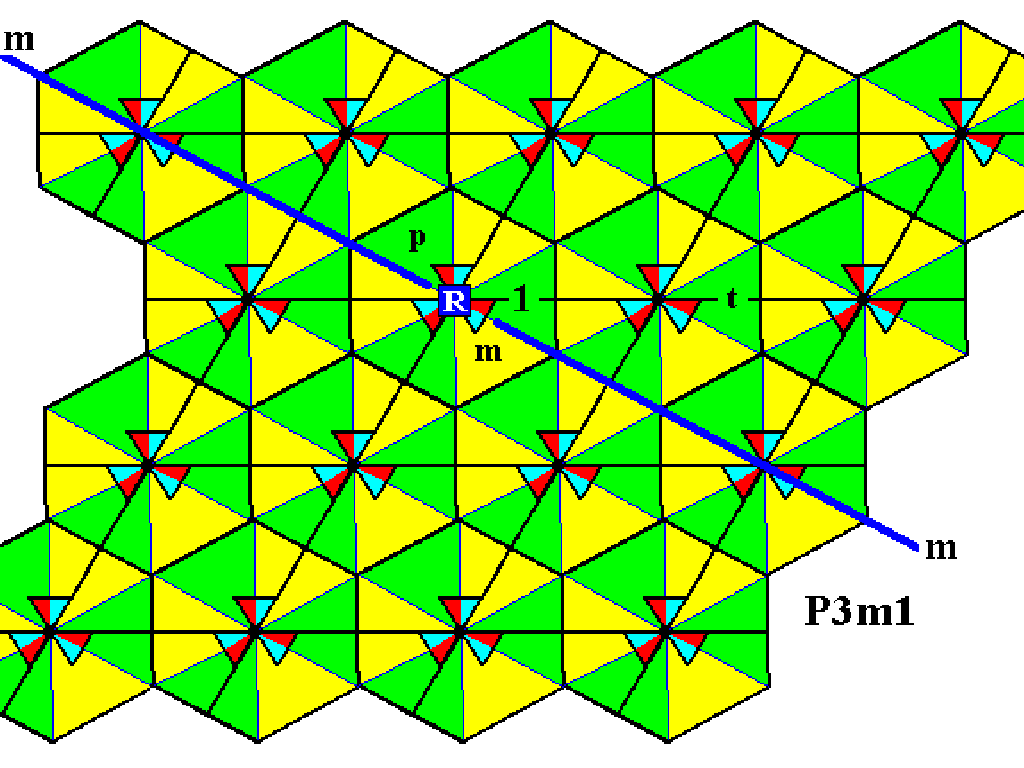
While generating the group elements (represented by triangular areas of the same size, that tesselate the plane completely) of the Group P3m1 , we will use an enlargement of the Figures used in the previous document in order to have more space for the notation of group elements.

Figure 1. Magnification of the last Figure of the previous document (Figure 24).
In the partitioned P3m1 pattern four group elements (represented by triangular areas) are explicitly indicated :
The initial element 1 .
The generator p .
The generator m .
The generator t .

In the next Figure we generate the elements p² , pm, and p²m by (repeatedly) applying the generator p , which is an anticlockwise rotation of 120⁰ about the point R .

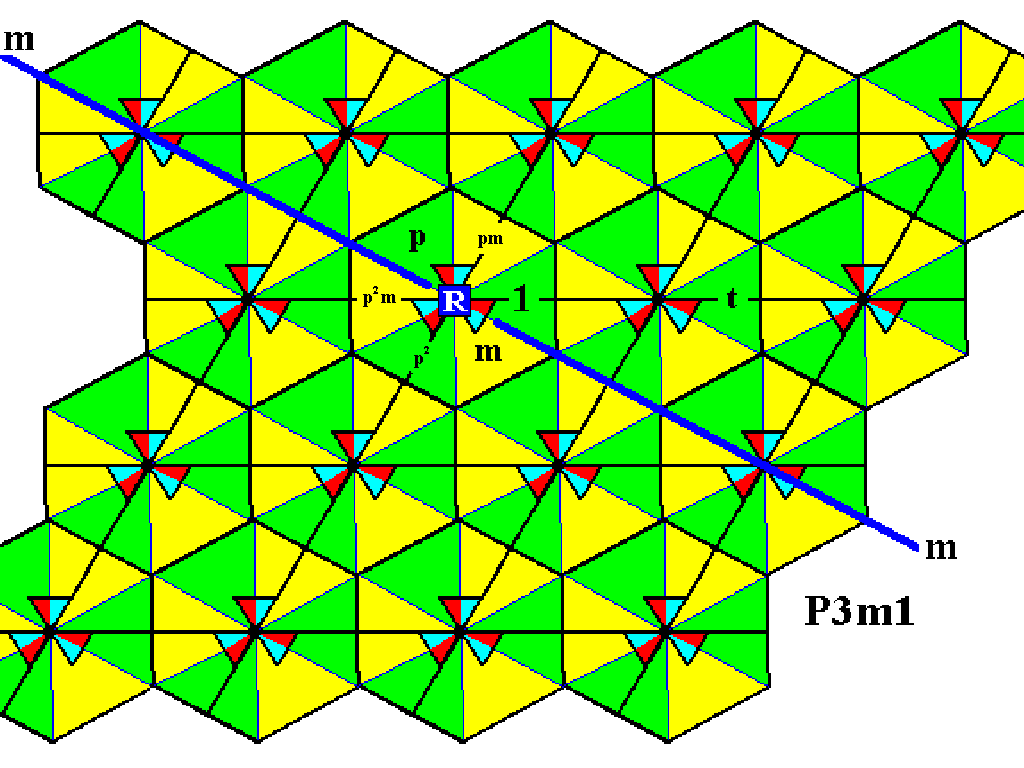
Figure 2. Generation of some new group elements of the Plane Group P3m1 .

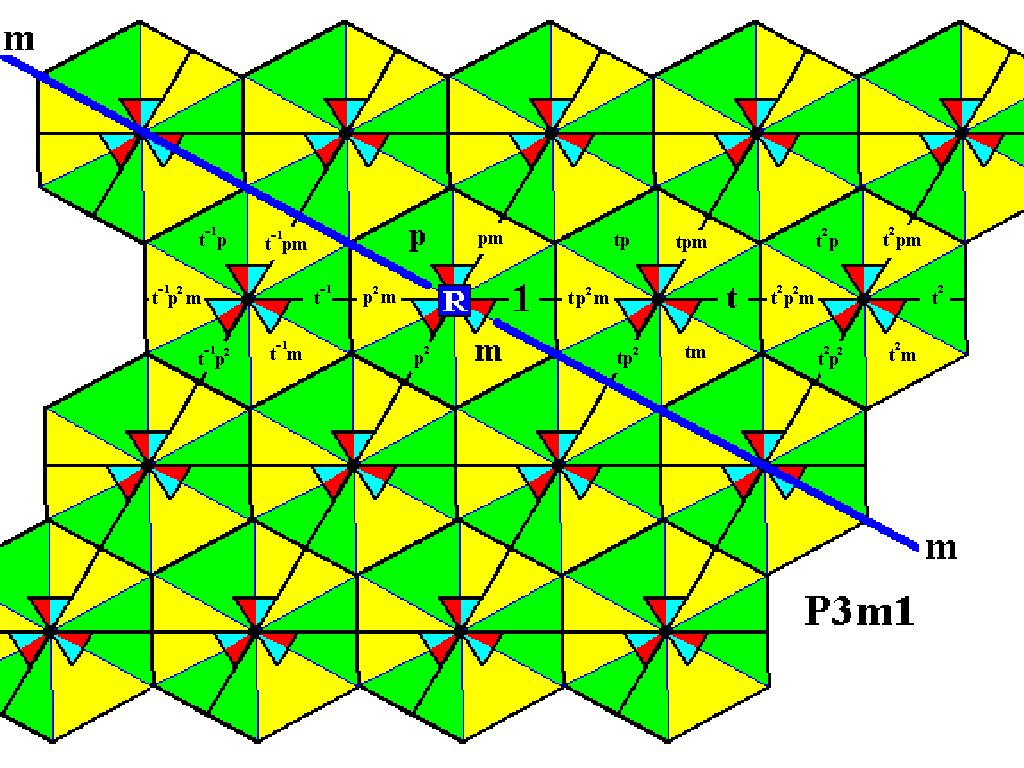
Figure 3. By means of (repeatedly) applying the generator t the group elements involved in the second row of motifs s.l. are generated.

The next Figure shows that a rotation about the point R can reach the first and third rows of motifs s.l.

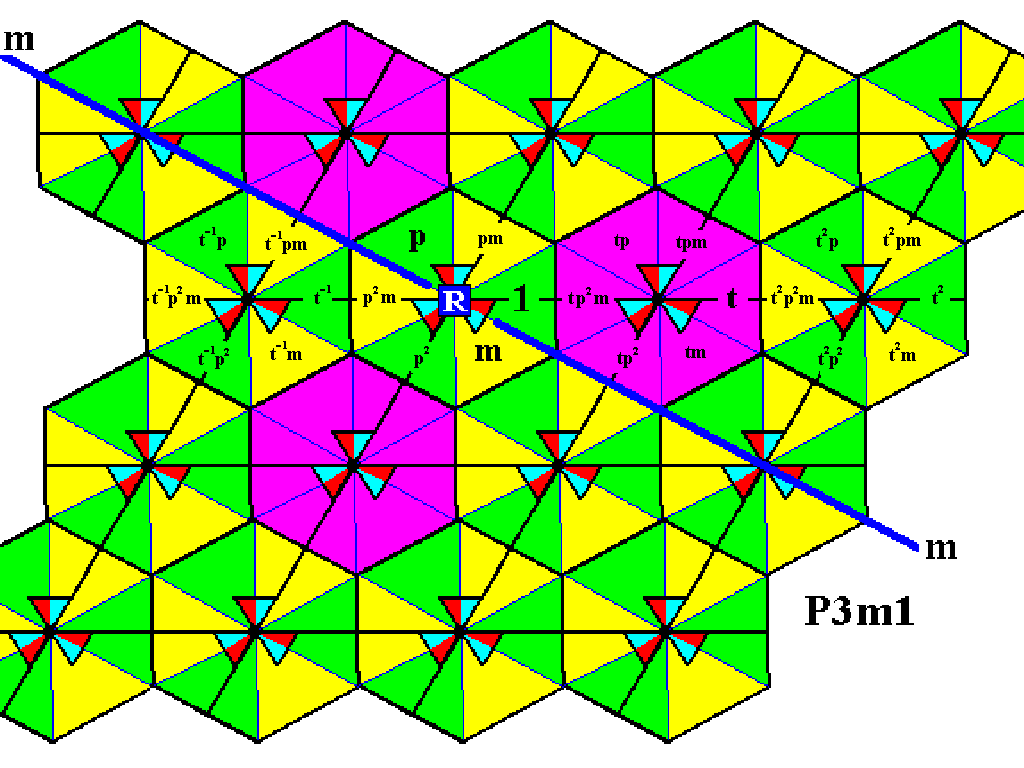
Figure 4. Indication of the effect of rotation about the three-fold axis at the point R of the elements around the lattice point next to R to its right. The possible rotations are represented by the elements p and p² , which are anticlockwise rotations of resp. 120⁰ and 240⁰ about the point R . See also next Figure for a better overview.

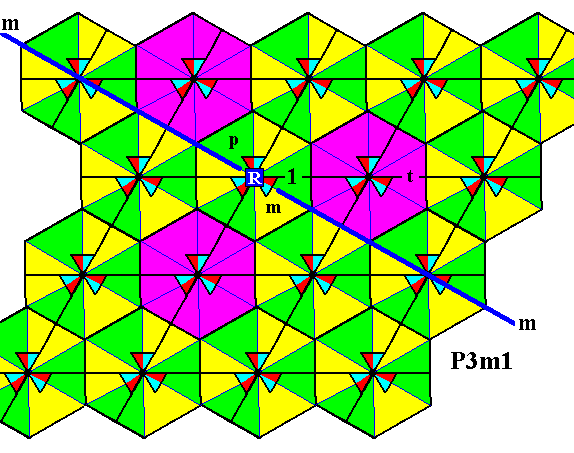
Figure 5. Smaller scale image of the presently used pattern representing the Group P3m1 , also showing the possibility of generating new group elements by rotation about the point R .

The next Figure generates the group elements that result from the above mentioned rotations of the elements situated around the lattice point next right to the lattice point R .

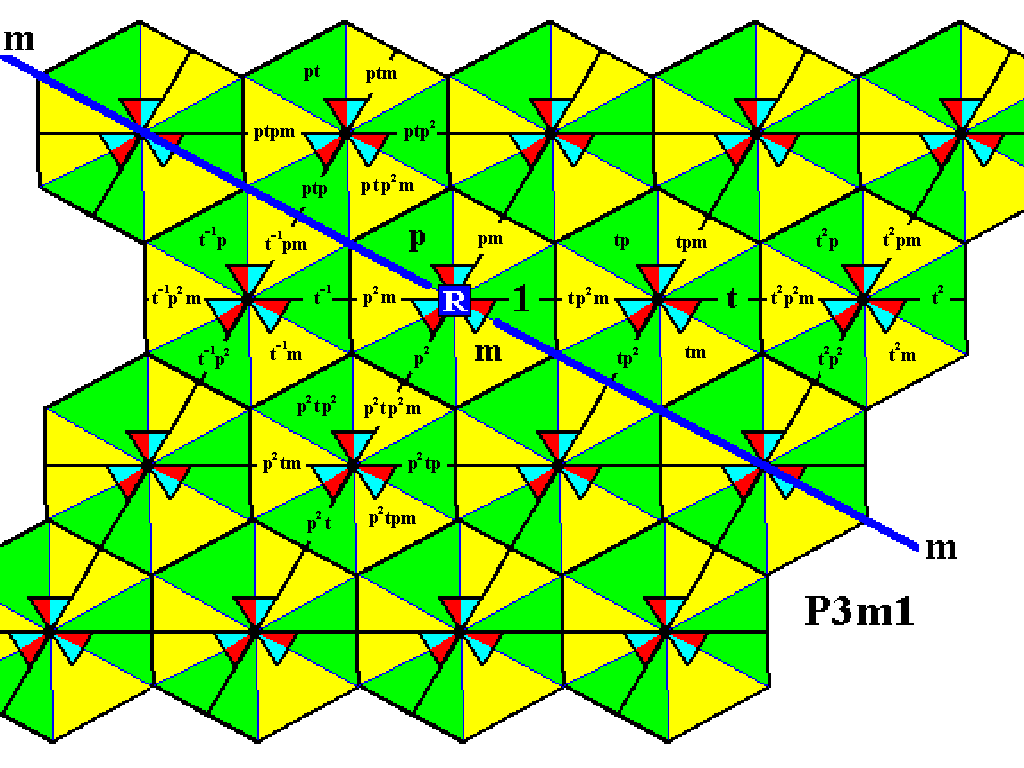
Figure 6. The first and third rows of motifs s.l. have been reached by means of the above mentioned rotations about the point R .

The first and third rows can now be completed by (repeatedly) applying the generator t (and its inverse t^-1 ) :

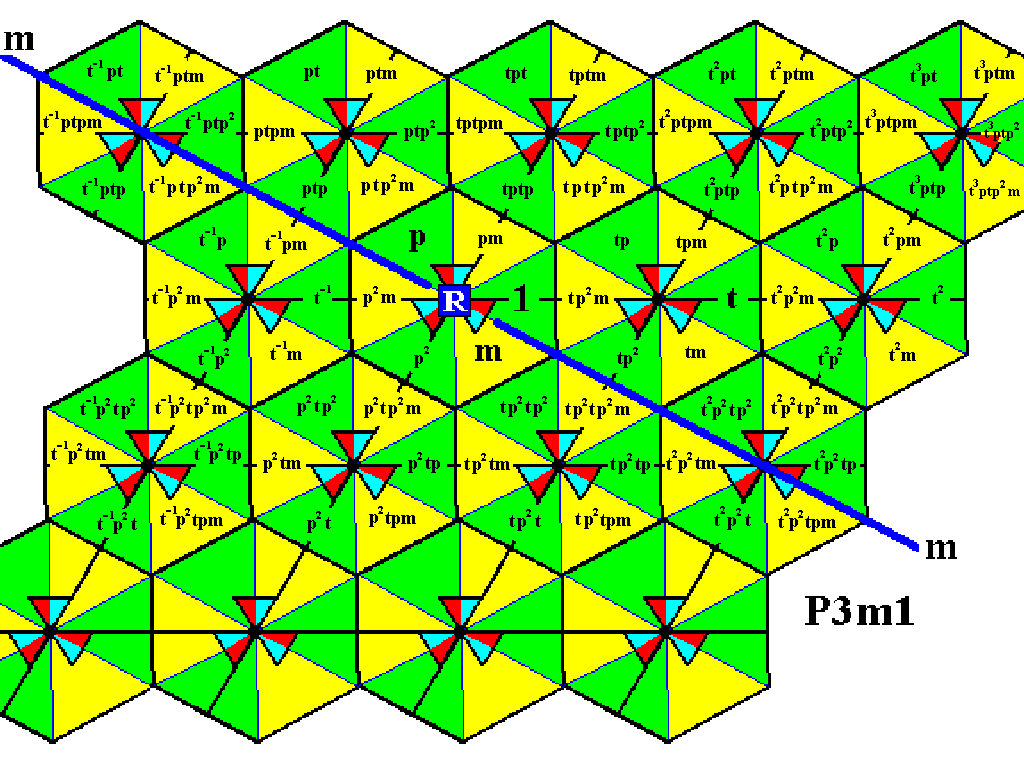
Figure 7. Completion of the first and third rows of the motifs s.l. of the pattern according to the Plane Group P3m1 .

Next we will again use the rotation p² in order to obtain group elements of the fourth row of motifs s.l. This rotation is indicated in the next Figure.

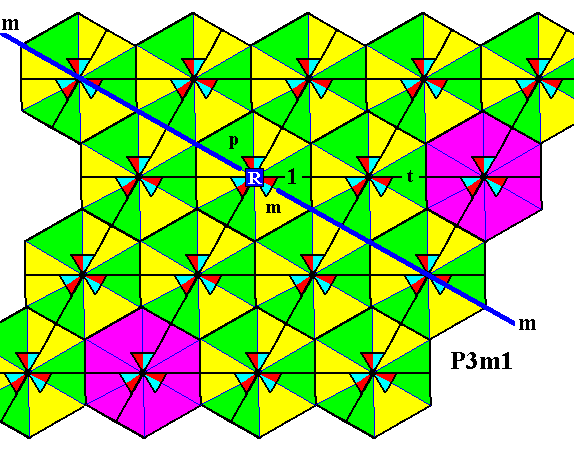
Figure 8. We can reach the fourth row of motifs s.l. of our P3m1 pattern, by rotating the elements of the last motif s.l. of the second row, about the point R 240⁰ anticlockwise, which is equivalent to applying p² .

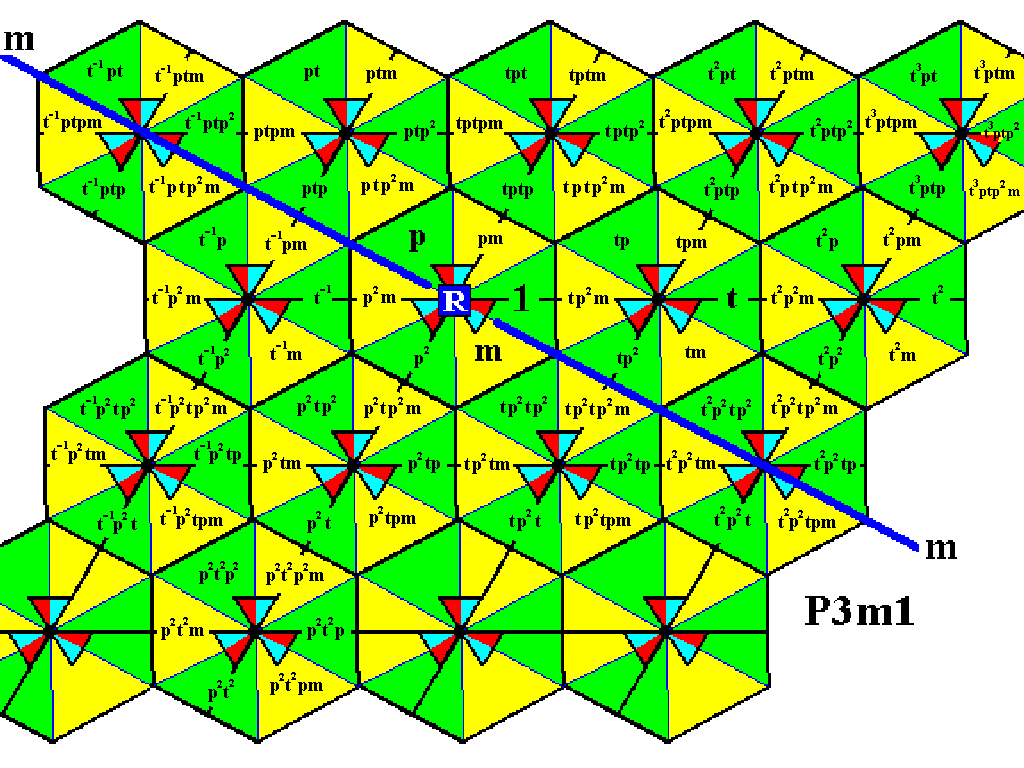
Figure 9. Reaching the fourth row of motifs s.l. of our P3m1 pattern by means of the rotation p² of the elements of the last motif s.l. of the second row.

This fourth row can now be completed by applying translations to the lastly obtained group elements :

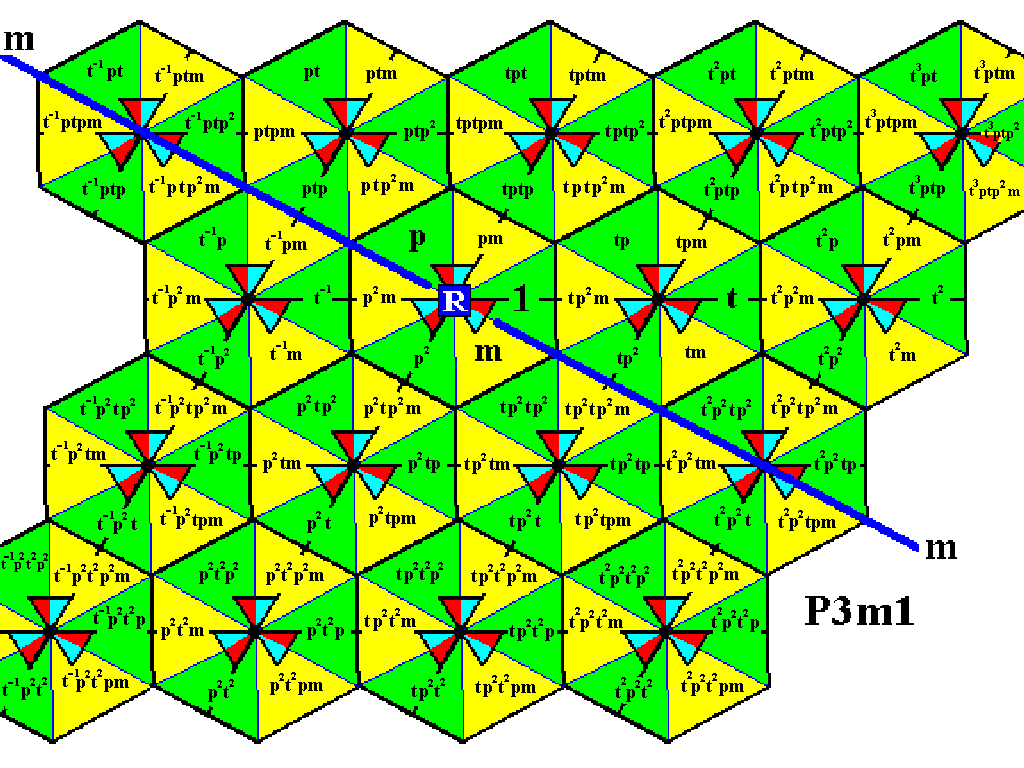
Figure 10. Completion of the fourth row of motifs s.l. of our P3m1 pattern.

We have now generated all group elements of the displayed part of the P3m1 pattern. But because the group is infinite, the generation process should go on indefinitely.

In the next document we will generate the group elements of the Plane Group P31m.

e-mail :