Wholeness and the Implicate Order
The Crystallization Process and the Implicate Order
(Part Eighteen)
We  continue our investigation concerning the generation of group elements of the Plane Groups.
The Plane Group P6mm (Sequel)

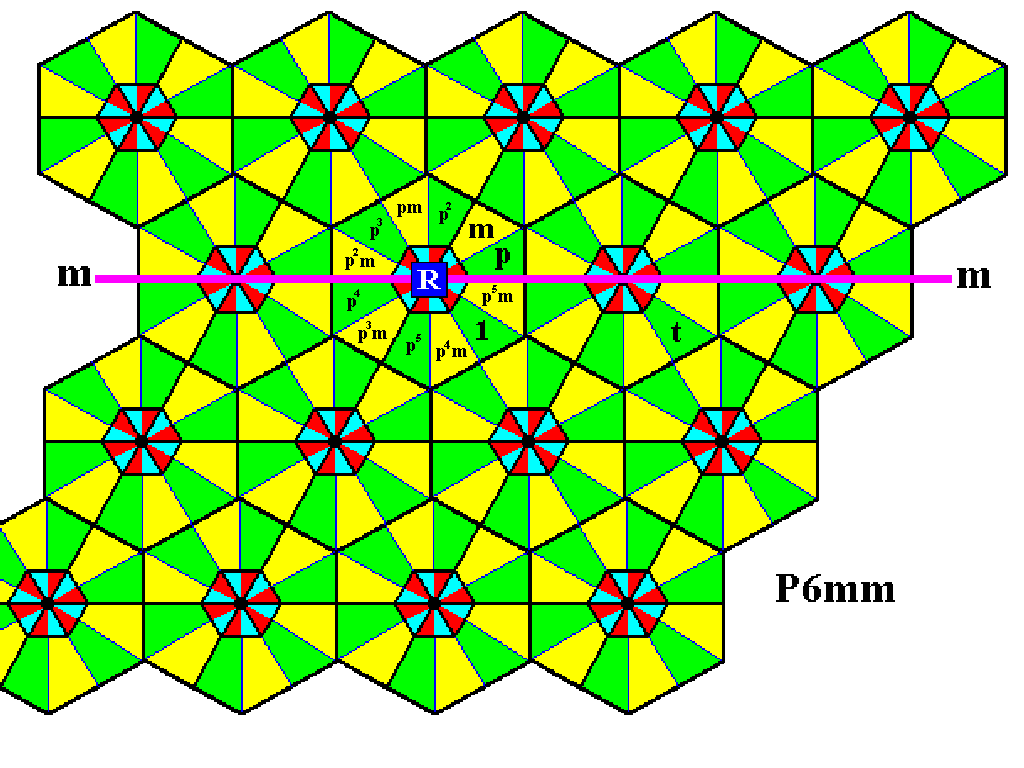
The next Figure shows the generation of all the remaining group elements of the composed motif s.l. at the lattice point  R .

Figure 1.  Generation of the remaining group elements represented by the basic units of the motif s.l. at the lattice point  R .
The second row of motifs s.l. of the  P6mm  pattern can now be completed by means of translations :

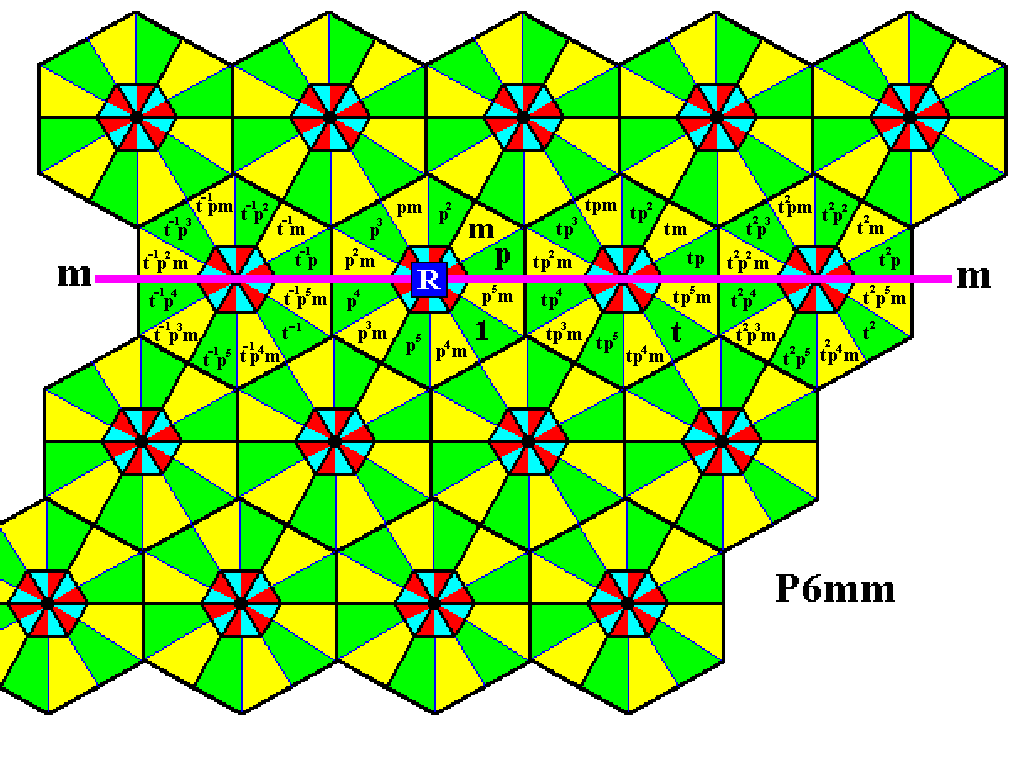
Figure 2.  Completion of the filling-in of group elements of the second row of motifs s.l. of the  P6mm  pattern.
The next Figure indicates how the first and third rows of the motifs s.l. of our  P6mm  pattern can be reached by rotations.

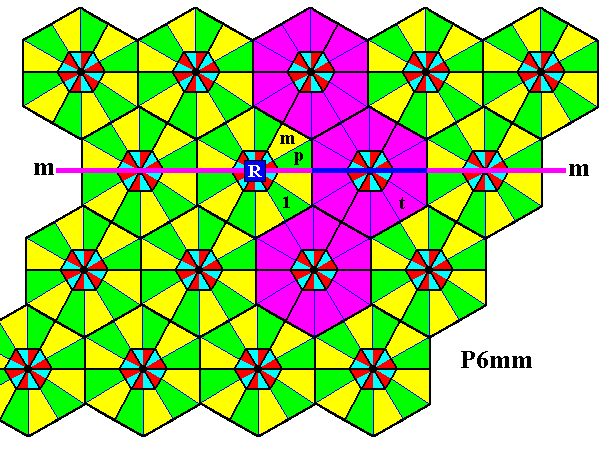
Figure 3.  The first and third rows of motifs s.l. can be reached by rotations about the point  R  of the elements making up the composed motif s.l. at the lattice point right next to the lattice point  R  :
To reach the first row, we use an anticlockwise rotation of 600 about the point  R ,  represented by the transformation  p .
To reach the third row, we can use an anticlockwise rotation of 3000 about the point  R ,  represented by the transformation  p5 .

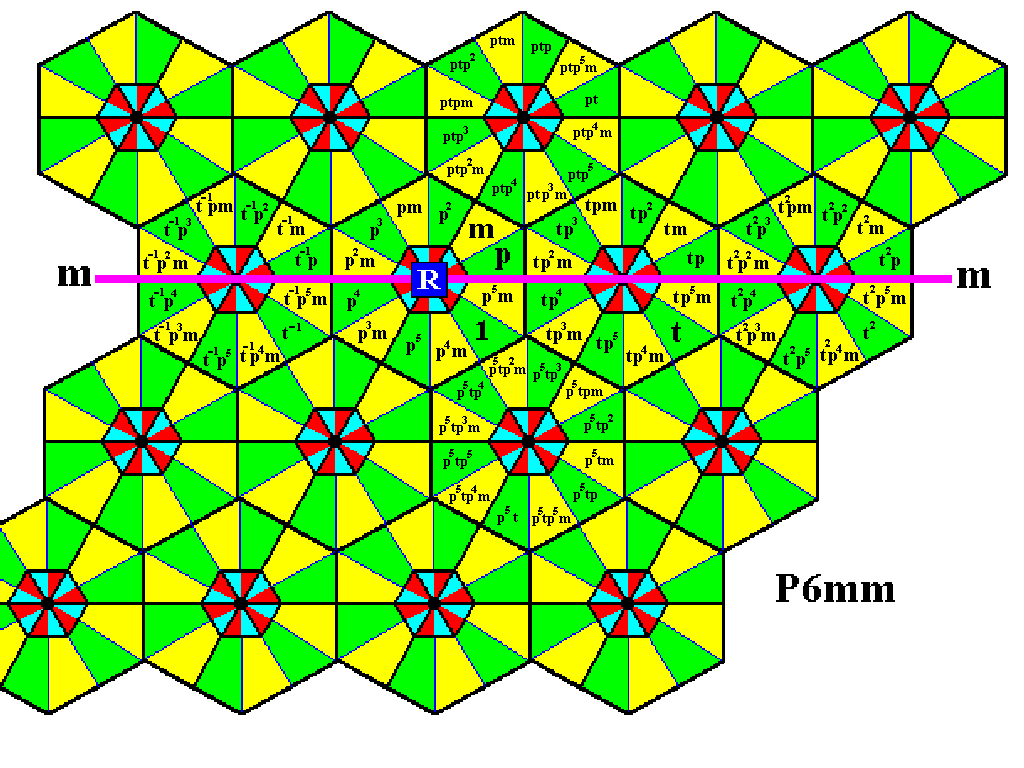
Figure 4.  The first and third rows have been reached, and the involved group elements generated.
The fourth row can also be reached by a rotation of already generated elements, namely by rotating the elements that make up the last composed motif s.l. of the second row. When we rotate these elements anticlockwise by 3000 about the point  R ,  then we will reach the fourth row. The next Figure indicates this rotation.

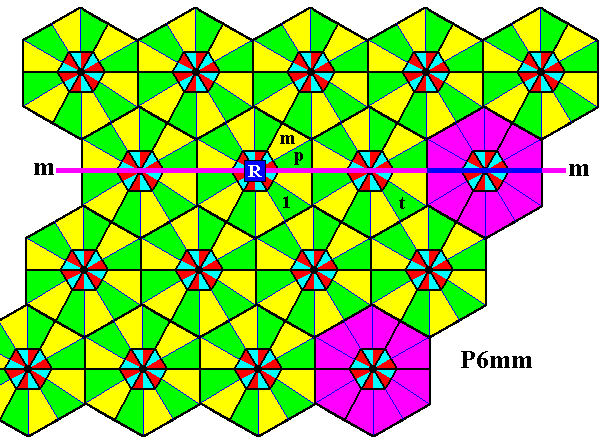
Figure 5.  Indication how to reach the fourth row by applying the transformation  p5  to the elements of the last motif s.l. of the second row.

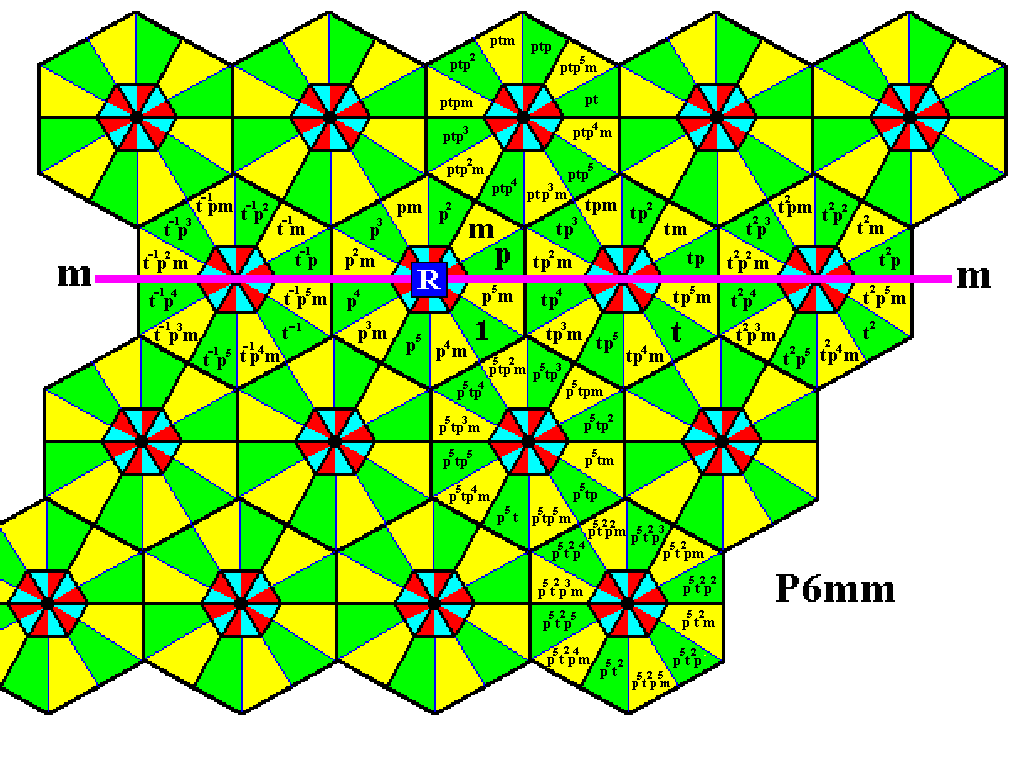
Figure 6.  The fourth row has been reached, and the involved group elements are generated.
The first, third, and fourth rows can now be completed by means of translations.
In order to do so we're going to assign concise labels to the areas representing group elements, because graphically they do not provide enough space for the group element symbols to be insered (And if we magnify the pattern still more, then we cannot have a convenient overview). We begin with labeling the lattice nodes (lattice points) with the letters

A,  B,  C,  D,  E,  F,  R,  G,  H,  I,  J,  K,  L,  M,  N,  O,  P.

Each such lattice node is associated with twelve triangular areas representing group elements. These areas are numbered

1,  2,  3,  4,  5,  6,  7,  8,  9,  10,  11,  12,

for every lattice node.
We now explain how to read the labels of these areas.

The twelve areas associated with the lattice node  A  must be read as

A1,  A2,  A3,  A4,  A5,  A6,  A7,  A8,  A9,  A10,  A11,  A12.

The twelve areas associated with the lattice node  B  must be read as

B1,  B2,  B3,  B4,  B5,  B6,  B7,  B8,  B9,  B10,  B11,  B12.

And so on.
An exception to this procedure is represented by the fact that we label the generators  p, m  and  t  with their proper symbols,  p, m  and  t . Also the initial element will be adressed by its proper symbol  1  (instead of R1). So the twelve areas associated with the lattice point  R  are given as

1  (initial element, identity element),  R2,  p,  m,  R5,  R6,  R7,  R8,  R9,  R10,  R11,  R12.

The areas associated with the lattice point  G  are then given by

t,  G2,  G3,  G4,  G5,  G6,  G7,  G8,  G9,  G10,  G11,  G12..

The next Figure illustrates this labeling, and is followed by a table that connects the labels with the corresponding generative symbols for the group elements.

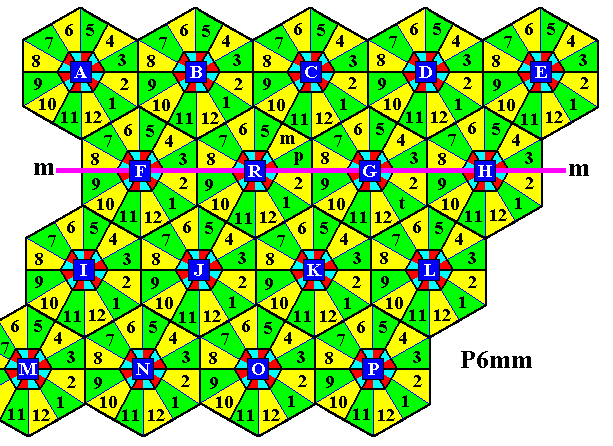
Figure 7.  Labeling of the areas of the  P6mm  pattern, representing group elements. The tabel below relates these labels with the true group element symbols. The initial element and the generator elements have as their label directly their true group element symbol.
In the next Table we give all group elements (and their corresponding labels) of the displayed part of our  P6mm  pattern, thus including the ones that have already been determined above. These latter will be displayed with white symbols, while the newly generated group elements -- obtained by completing the first, third and fourth rows by applying translations -- will be given in red.

Table of Labels and Group Element Symbols, referring to Figure 7

Label Group element   Label Group element   Label Group element
A1 t-2ptp5   A2 t-2ptp4m   A3 t-2pt
A4 t-2ptp5m   A5 t-2ptp   A6 t-2ptm
A7 t-2ptp2   A8 t-2ptpm   A9 t-2ptp3
A10 t-2ptp2m   A11 t-2ptp4   A12 t-2ptp3m
               
B1 t-1ptp5   B2 t-1ptp4m   B3 t-1pt
B4 t-1ptp5m   B5 t-1ptp   B6 t-1ptm
B7 t-1ptp2   B8 t-1ptpm   B9 t-1ptp3
B10 t-1ptp2m   B11 t-1ptp4   B12 t-1ptp3m
               
C1 ptp5   C2 ptp4m   C3 pt
C4 ptp5m   C5 ptp   C6 ptm
C7 ptp2   C8 ptpm   C9 ptp3
C10 ptp2m   C11 ptp4   C12 ptp3m
               
D1 tptp5   D2 tptp4m   D3 tpt
D4 tptp5m   D5 tptp   D6 tptm
D7 tptp2   D8 tptpm   D9 tptp3
D10 tptp2m   D11 tptp4   D12 tptp3m
               
E1 t2ptp5   E2 t2ptp4m   E3 t2pt
E4 t2ptp5m   E5 t2ptp   E6 t2ptm
E7 t2ptp2   E8 t2ptpm   E9 t2ptp3
E10 t2ptp2m   E11 t2ptp4   E12 t2ptp3m
               
F1 t-1   F2 t-1p5m   F3 t-1p
F4 t-1m   F5 t-1p2   F6 t-1pm
F7 t-1p3   F8 t-1p2m   F9 t-1p4
F10 t-1p3m   F11 t-1p5   F12 t-1p4m
               
1 1   R2 p5m   p p
m m   R5 p2   R6 pm
R7 p3   R8 p2m   R9 p4
R10 p3m   R11 p5   R12 p4m
               
G1 t   G2 tp5m   G3 tp
G4 tm   G5 tp2   G6 tpm
G7 tp3   G8 tp2m   G9 tp4
G10 tp3m   G11 tp5   G12 tp4m
               
H1 t2   H2 t2p5m   H3 t2p
H4 t2m   H5 t2p2   H6 t2pm
H7 t2p3   H8 t2p2m   H9 t2p4
H10 t2p3m   H11 t2p5   H12 t2p4m
               
I 1 t-2p5tp   I 2 t-2p5tm   I 3 t-2p5tp2
I 4 t-2p5tpm   I 5 t-2p5tp3   I 6 t-2p5tp2m
I 7 t-2p5tp4   I 8 t-2p5tp3m   I 9 t-2p5tp5
I 10 t-2p5tp4m   I 11 t-2p5t   I 12 t-2p5tp5m
               
J1 t-1p5tp   J2 t-1p5tm   J3 t-1p5tp2
J4 t-1p5tpm   J5 t-1p5tp3   J6 t-1p5tp2m
J7 t-1p5tp4   J8 t-1p5tp3m   J9 t-1p5tp5
J10 t-1p5tp4m   J11 t-1p5t   J12 t-1p5tp5m
               
K1 p5tp   K2 p5tm   K3 p5tp2
K4 p5tpm   K5 p5tp3   K6 p5tp2m
K7 p5tp4   K8 p5tp3m   K9 p5tp5
K10 p5tp4m   K11 p5t   K12 p5tp5m
               
L1 tp5tp   L2 tp5tm   L3 tp5tp2
L4 tp5tpm   L5 tp5tp3   L6 tp5tp2m
L7 tp5tp4   L8 tp5tp3m   L9 tp5tp5
L10 tp5tp4m   L11 tp5t   L12 tp5tp5m
               
M1 t-3p5t2p   M2 t-3p5t2m   M3 t-3p5t2p2
M4 t-3p5t2pm   M5 t-3p5t2p3   M6 t-3p5t2p2m
M7 t-3p5t2p4   M8 t-3p5t2p3m   M9 t-3p5t2p5
M10 t-3p5t2p4m   M11 t-3p5t2   M12 t-3p5t2p5m
               
N1 t-2p5t2p   N2 t-2p5t2m   N3 t-2p5t2p2
N4 t-2p5t2pm   N5 t-2p5t2p3   N6 t-2p5t2p2m
N7 t-2p5t2p4   N8 t-2p5t2p3m   N9 t-2p5t2p5
N10 t-2p5t2p4m   N11 t-2p5t2   N12 t-2p5t2p5m
               
O1 t-1p5t2p   O2 t-1p5t2m   O3 t-1p5t2p2
O4 t-1p5t2pm   O5 t-1p5t2p3   O6 t-1p5t2p2m
O7 t-1p5t2p4   O8 t-1p5t2p3m   O9 t-1p5t2p5
O10 t-1p5t2p4m   O11 t-1p5t2   O12 t-1p5t2p5m
               
P1 p5t2p   P2 p5t2m   P3 p5t2p2
P4 p5t2pm   P5 p5t2p3   P6 p5t2p2m
P7 p5t2p4   P8 p5t2p3m   P9 p5t2p5
P10 p5t2p4m   P11 p5t2   P12 p5t2p5m
So we have now generated all group elements of the displayed part of the  P6mm  pattern.
And this was the last Plane Group of the total of 17.
In the next -- and last -- document devoted to the 'noetic crystallization process' of two-dimensional crystals, we will summarize these 17 basic patterns as they are exhaustively partitioned in areas that represent group elements.

e-mail : 
To continue click HERE for further study of the totally dynamic and holistic nature of Reality.
back to homepage

back to Introduction

back to the Ink-in-Glycerine Model

back to Part I of The Crystallization process and the Implicate Order

back to Part II of The Crystallization process and the Implicate Order

back to Part III of The Crystallization process and the Implicate Order

back to Part IV of The Crystallization process and the Implicate Order

back to Part V of The Crystallization process and the Implicate Order

back to Part VI of The Crystallization process and the Implicate Order

back to Part VII of The Crystallization process and the Implicate Order

back to Part VIII of The Crystallization process and the Implicate Order

back to Part IX of The Crystallization process and the Implicate Order

back to Part X of The Crystallization process and the Implicate Order

back to Part XI of The Crystallization process and the Implicate Order

back to Part XII of The Crystallization process and the Implicate Order

back to Part XIII of The Crystallization process and the Implicate Order

back to Part XIV of The Crystallization process and the Implicate Order

back to Part XV of The Crystallization process and the Implicate Order

back to Part XVI of The Crystallization process and the Implicate Order

back to Part XVII of The Crystallization process and the Implicate Order

****************