We will now investigate the generation of the Plane Group Pg, i.e. the generation of its group elements.
The Plane Group Pg
We're now going to generate the group elements of the Plane Group Pg.
We first let the motif units composing the motifs s.str. represent the group elements. Then we determine the motif units of the motif s.l. and let them represent the group elements, and generate the latter again.
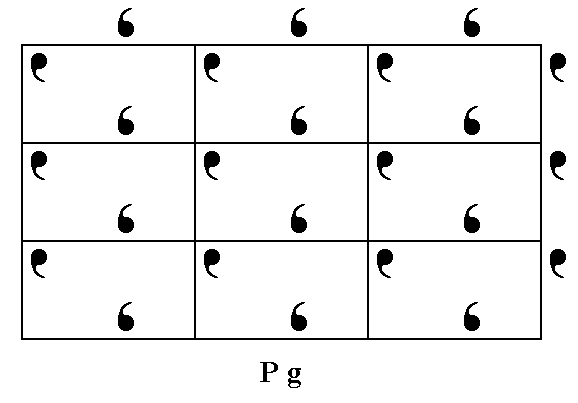
Figure 1. Assymmetric motifs (in fact motif units) placed in a primitive rectangular net, such that they alternate along the y edges (horizontal) of the meshes, produce a pattern that represents the Plane Group Pg .
The only symmetry elements the Plane Group Pg possesses, are simple translations (in the x (vertical) and y (horizontal) directions) and glide lines parallel to the y direction.
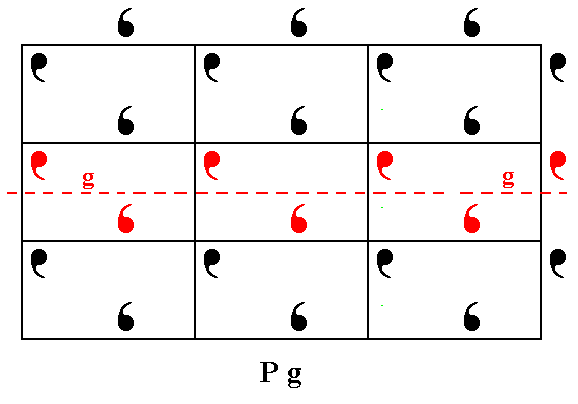
Figure 2. Patterns representing Plane Group Pg have glide lines parallel to the y direction. One of them is shown.
The total symmetry content of the Plane Group Pg is shown in the next Figure.
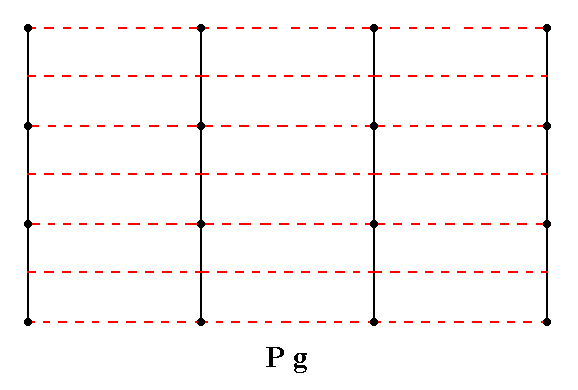
Figure 3. Total symmetry content of the Plane Group Pg.
Glide lines are indicated by red dashed lines. For clarity the nodes of the net are indicated (black dots).
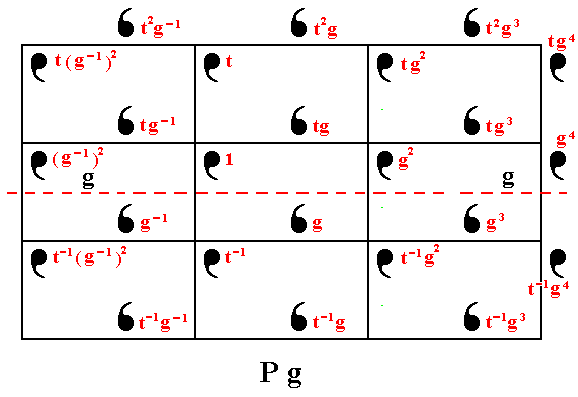
Figure 4. The pattern representing Plane Group Pg consists of motif units (commas). They can be generated from a given initial motif unit, denoted 1 , by two generators g (a horizontal glide reflection) and t (a vertical translation).
When we remove all translations, the individuals of the same type of motif unit will be superimposed upon each other, resulting in only one individual per type. In the present case this means that only two individuals remain, one of each type (= the two types of comma in our Figures), and these two individuals become aligned to each other because of the disappearance of translational distances, and in this way together form a figure that has point symmetry m. Thus the Point Group to which our Plane Group belongs is m. See Figure 5.
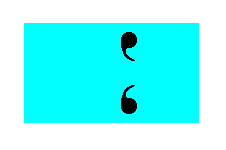
Figure 5. The translation-free residue of the pattern representing Plane Group Pg has m symmetry (i.e. the only symmetry element it has is one mirror line), and represents the Point Group to which the Plane Group Pg belongs.
The next Figure shows what the very motif (s.str.) actually is, and that it is constituted out of two motif units. This motif, together with its surroundings (such that together they make up the motif s.l.), tiles the 2-D plane completely (shown in Figures 7 and 8).
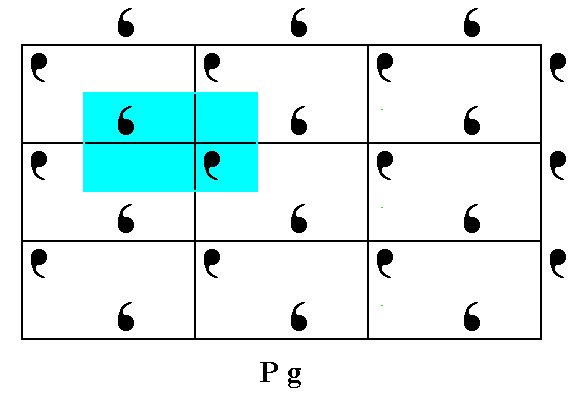
Figure 6. The real motif, constituting the pattern of Figure 1.
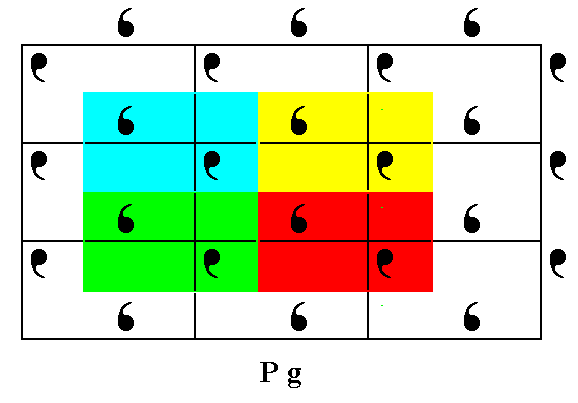
Figure 7. The real motif s.l. tiles the entire 2-D plane in a periodic fashion.
The next Figure depicts a more extensive tiling (tesselation) of the same motifs s.l. of our Pg pattern, while two colors are being used.

Figure 8. Tesselation of the 2-D plane with motifs s.l. of the Pg pattern of Figure 1 .
Our Pg pattern contains motif units (commas) as parts of a motif s.str. Such a motif s.str. consists of two of the mentioned motif units (commas), and these units are drawn apart by the glide reflection, which separates the two units (of each motif s.str.) by its translational component.

Figure 9. The red and blue elongate rectangles represent the group elements of the Pg pattern of Figure 1. Each such a rectangle contains one motif unit (of the motif s.str.).
The next Figure is the same as the previous Figure, but now with the initial element 1 and the two generator elements indicated and highlighted.

Figure 10. Areas of the Pg pattern of Figure 1 corresponding to the group elements. The initial element 1 and the two generators g and t indicated and highlighted (purple).
All elements of the Group Pg can be generated from the initial element, by subjecting it (repeatedly) to the generator elements :

Figure 11. The group elements (g-1)2 (= g-2), (g-1)3 (= g-3), g-1 , g2 , g3 , g4 are generated from the initial element 1 by (repeatedly) applying the transformation g .
The rest of the group elements (of the depicted part) of our Pg pattern can be generated by applying the vertical translation t and its inverse t-1 to the already generated elements :
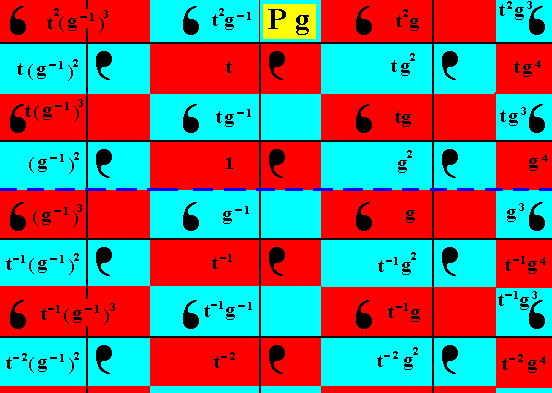
Figure 12. The group elements t2(g-1)3 , t(g-1)2 , , t-1(g-1)2 ,
t-1(g-1)3 , t-2(g-1)2 , t2g-1 , tg-1 , t-1 , t-1g-1 , t-2 , t2g , tg2 , tg , t-1g2 , t-1g ,
t-2g2 , t2g3 , tg4 , tg3 , t-1g4 , t-1g3 , t-2g4 , are generated from the already obtained group elements, by applying (repeatedly) the vertical translation t and its inverse t-1 .
The colors blue and red do not signify qualitative differences.
We have thus generated the group elements of the Group Pg ( The process must of course be continued indefinitely because the group is infinite).
The Plane Group P2mm
We're now going to generate the group elements of the Plane Group P2mm.
As before we first let the motif units composing the motifs s.str. represent the group elements. Then we determine the motif units of the motif s.l. and let them represent the group elements, and generate the latter again.
Figure 13. Placing motifs with 2mm point symmetry in a primitive rectangular 2-D lattice creates a periodic pattern of these motifs representing the Plane Group P2mm. The pattern must be conceived as extending indefinitely in two-dimensional space.
The total symmetry content of this Plane Group is given in Figure 14.
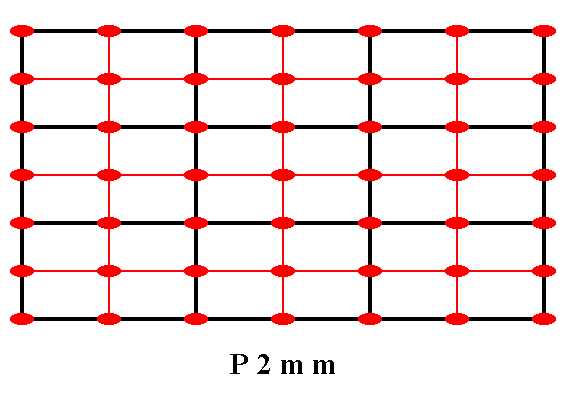
Figure 14. The total symmetry content of the Plane Group P2mm.
Solid lines (black and red) indicate mirror lines.
Small red solid ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
The next Figure again gives the P2mm patttern, and prepares for letting it be generated.
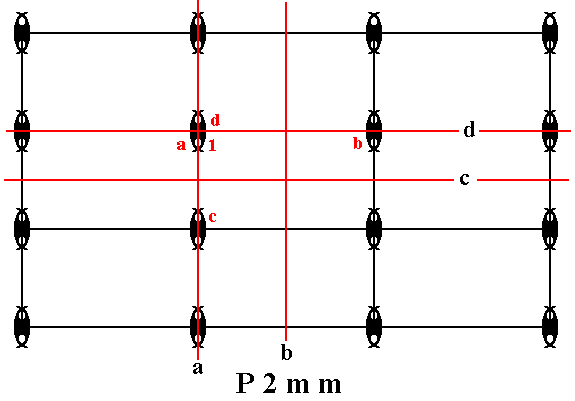
Figure 15. Each (composed) motif of our version of a P2mm pattern consists of four motif units (commas) partially overlapping, such that the symmetry of the resulting composed motif is 2mm . As before, each motif unit represents a group element.
One such motif unit is chosen to be the initial motif unit, representing the identity element of the group, and denoted 1 .
A second motif unit, denoted a , is chosen as a first generator. It is produced from 1 by the mirror line a .
A third motif unit, denoted b , is chosen as a second generator. It is produced from 1 by the mirror line b .
A fourth motif unit, denoted c , is chosen as a third generator. It is produced from 1 by the mirror line c .
Finally, a fifth motif unit, denoted d , is chosen as a fourth generator. It is produced from 1 by the mirror line d .
The next Figure shows how the motif units -- representing group elements of the group P2mm -- are generated by the generators a, b, c and d .
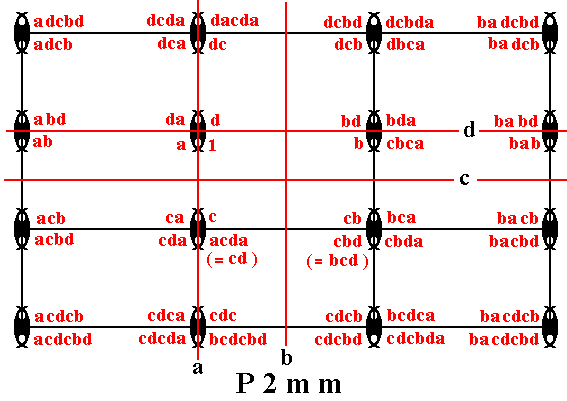
Figure 16. Generation of the group elements of the group P2mm by the generators a, b, c, d .
The next Figure shows the motifs s.l. and how they tesselate the plane.
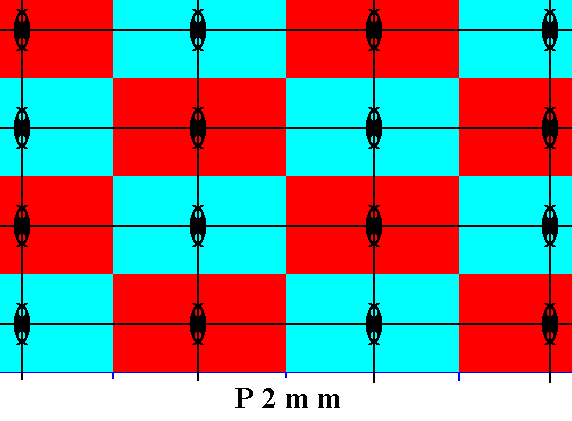
Figure 17. Motifs s.l. (red and blue rectangles) of the P2mm pattern of Figure 13. Each such motif s.l. consists of one motif s.str. (itself consisting of four partly overlapping motif units (commas)), PLUS its corresponding background area. And each motif s.l. is associated with a lattice point.
(The colors red and blue do not signify qualitative differences).
The next Figure depicts the areas (of our pattern) representing group elements.
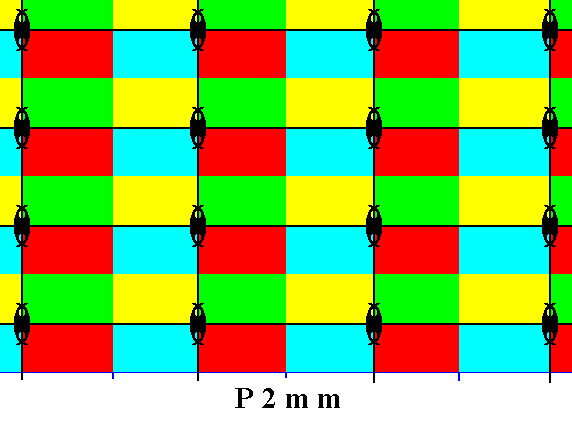
Figure 18. The motifs s.l. of our P2mm pattern consist of four smaller rectangular areas each representing a different group element.
The next Figure is the same as Figure 18, but now with the symmetry elements of the four generators (four mirror reflections) inserted.
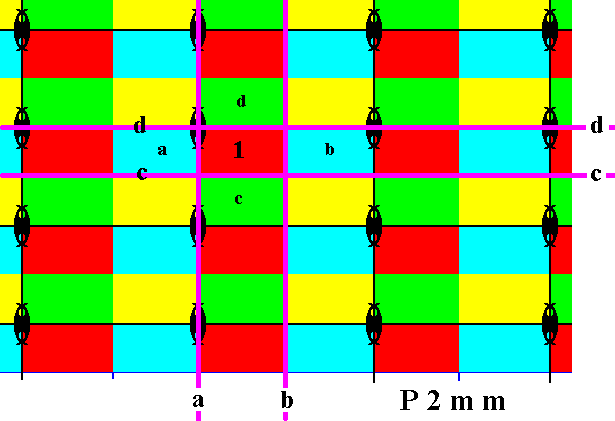
Figure 19. Group elements represented by (smaller) rectangular areas of the P2mm pattern of Figure 13 . Each such a group element representative contains one quarter of a motif s.str. PLUS a corresponding background area. The symmetry elements of the four generators are indicated : four mirror lines, a, b, c, d . Also indicated are : The group elements representing the initial element, 1 , and those four generator elements, a, b, c, d .
( The different colors of the rectangles do not signify qualitative differences).
The next Figure shows some elements generated from the given elements by applying the horizontal reflections.
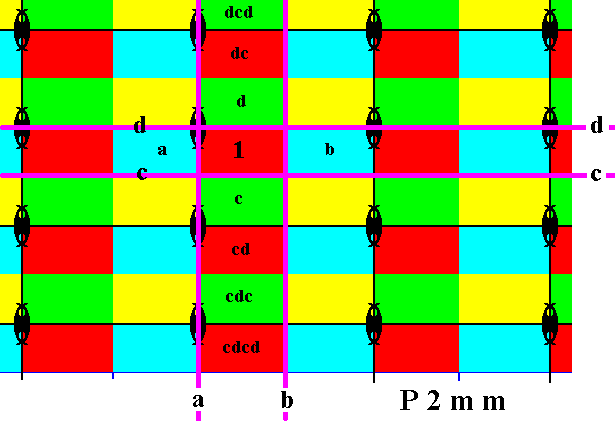
Figure 20. The group elements dc, cd, dcd, cdc, cdcd , are generated by subjecting the already given elements to the horizontal reflections c and d .
We can now obtain new group elements by applying the vertical reflection a to already generated or given group elements :
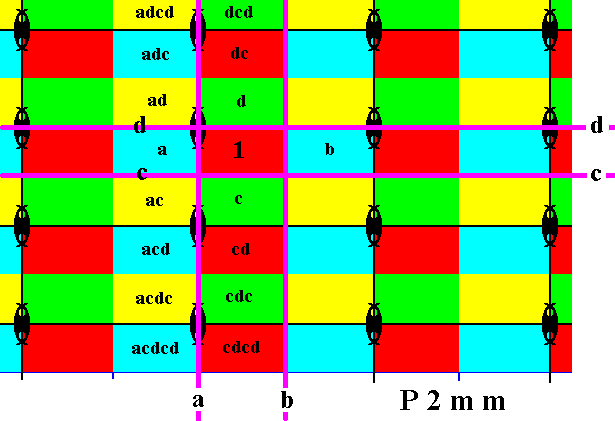
Figure 21. The group elements adcd, adc, ad, ac, acd, acdc, acdcd are generated by applying the reflection a to some elements already generated.
We can generate yet more group elements by applying the reflection b to the elements already generated :
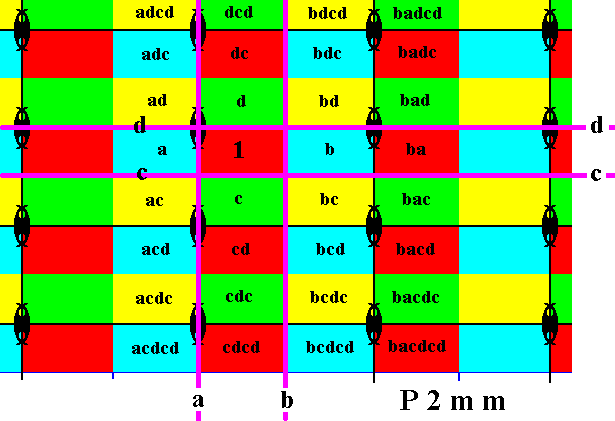
Figure 22. The group elements bdcd, bdc, bd, bc, bcd, bcdc, bcdcd, badcd, badc, bad, ba, bac, bacd, bacdc, bacdcd are generated by applying the reflection b to elements already generated.
To obtain still further group elements we can apply the reflection a to the elements of the last column but one :
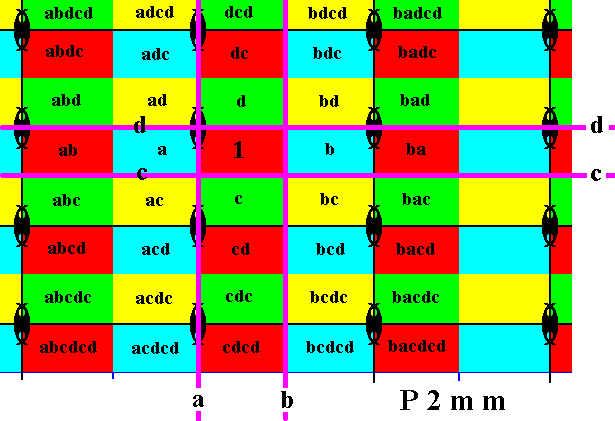
Figure 23. The group elements abdcd, abdc, abd, ab, abc, abcd, abcdc, abcdcd are generated by applying the reflection a to the elements of the last column but one.
When we subject the last obtained group elements to the reflection b we get yet another column of new group elements :
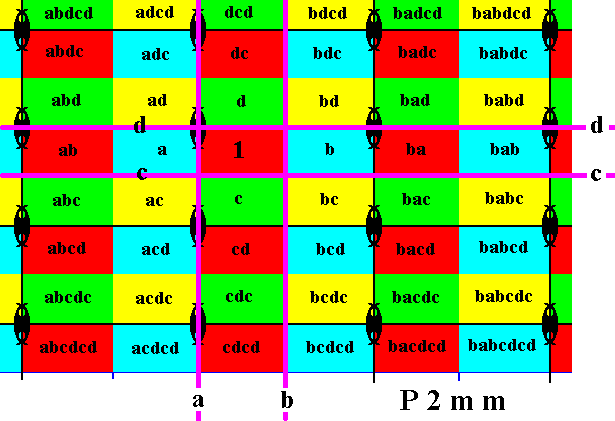
Figure 24. The group elements babdcd, babdc, babd, bab, babc, babcd, babcdc, babcdcd are generated by applying the reflection b to the elements of the extreme left column.
So we have now generated the group elements of the Group P2mm . Of course the generation process must continue indefinitely, because the Group is infinite.
In the next document we will continue with the Plane Group P2gg .
e-mail : 
To continue click HERE for further study of the totally dynamic and holistic nature of Reality.
back to homepage
back to the Ink-in-Glycerine Model
back to Part I of The Crystallization process and the Implicate Order
back to Part II of The Crystallization process and the Implicate Order