Introduction

In his main book on the theory of the Implicate Order Wholeness and the Implicate Order, 1980, BOHM presents his theory of wholeness. Apart from some general considerations, the book turns out to consist of two 'parts'.
One part is about the theory of hidden variables as proposed by BOHM. It deals with an alternative mathematical formalism involving hidden variables.
The second part is a more or less informal treatment of the theory of the implicate order, also involving quantum theory, and in addition relativity theory, in such a way that he shows that those two theories both point, each in their own way, to the wholeness of Reality. The theory of wholeness is further developed and set in a more or less broader context which is partly philosophical.
Well, although both parts are about the existence of more or less unknown lower levels of Reality that exert causal influences on higher levels, they are in a way kind of disparate :
In the first part no mention is made of the Implicate Order. Instead a series of sub-quantum levels is proposed, that could explain some of the known quantum features, and can eliminate the irreducible randomness (occurring at the quantum level) as it is according to current quantum theory, by postulating hidden variables residing in the sub-quantum levels. This hidden variable theory is such that (also) from it we can deduce the basic principles of current quantum mechanics, for example the indivisibility of the quantum of action, the uncertanty principle of Heisenberg, and so on. But the new theory restricts these principles to the quantum level. They do not necessarily apply to the sub-quantum levels. BOHM further remarks that his theory of hidden variables is far from complete, but sufficient to show that such a theory can sensibly be propesed to the physics community.
In the second part of Bohms book no explicit mention is made of these sub-quantum levels, instead the concept of the Implicate Order is elaborated, and, moreover, in a more qualitative and philosophical way. Emphasis has been put on the non-local character of the Implicate Order, and on the phenomenon of injection (enfoldment) and projection (unfoldment), i.e. the dynamics of implication and explication of structures. The theory of the Implicate Order is further elucidated by means of some clever analogies, like the ink-in-glycerine model, the fish tank, and the hologram.
So it seems that BOHM's theory of the Implicate Order is a bit different from his theory of hidden variables. The latter theory is meant to be a genuine physical theory, and BOHM proposes experiments which could reveal the sub-quantum level. These experiments must involve very short time intervals and high energies, which present technology probably cannot yet realize. One of the interesting features of the theory is that it could show a way out of some problems concerning infinities which seem to be inherent in the current quantum theory.
I get the impression that it is perhaps too early trying to set up a full-fledged sub-quantum theory (but of course everybody should be free to embark on such an enormous endeavour). For the time being it is perhaps more fruitful to develop the second part of BOHM's book about the Implicate Order (instead of the theory of hidden variables), as he himself has done in 1987 in a book called Science, Order, and Creativity, with co-author David PEAT. We ourselves will, in the present document, give a qualitative account of BOHM's theory of hidden variables (in which some foreknowledge of quantum mechanics is perhaps necessary, in order to be able to follow that account).
The rest of the coming documents will, however, be devoted to the theory of the Implicate Order (which will accordingly be more speculative and informal), and especially its relation with the Neoplatonic metaphysics of Plotinus, as he has laid it down in his Enneads in the third century.

Before we will speak about BOHM's quantum mechanical hidden variable theory, we will first consider those ideas of BOHM which do relate Quantum Mechanics to the Implicate Order in a direct way, i.e. not only discusses quantum theory as pointing to Reality as a whole, but how the specific idea of the Implicate Order should be brought into the quantum theory in order to remedy some important shortcomings of the latter, especially the fact that quantum theory does not describe time and process from within the theory itself.
In classical mechanics (dynamics) as well as in quantum theory we have theories which express themselves in terms of observable quantities, like position, momentum, energy, and so on. In classical mechanics these quantities always have definite values, also when we ourselves do not always know these values, either not at all or not exactly. However, in quantum theory matters are different. Let us explain. Some variables, quantum as well as classical, come in pairs, such that their combined dimensions are those of action, for instance the pair position and momentum, i.e. where, say, a particle is (its coordinates) and what it is doing (its velocity). While in classical mechanics -- valid approximately for objects consisting of many particles, i.e. macroscopic objects -- the value of both members of such a pair can be known simultaneously, in quantum theory, dealing with submicroscopical objects, they cannot. Only one can be known with relatively high precision at the expence of the precision of the value of the other one. It is even so that this is not only a not-knowing, but also a not-being, in the sense that if one such variable is precisely measured, the other one is IN ITSELF undetermined. The latter is in a state of superposition of all its possible values. To express this fact mathematically (and then to deduce more features from it) observable quantities are, in quantum theory, interpreted as operators.
An operator is a mathematical operation on a function. An example of such an operator is the derivative of a function. A derivative of a function determines the rate of change of the function. Suppose we have the position derivative  d/dx  of the function  x².  This derivative determines the rate of change of the height of the curve (which, in the present example, is a parabola) described by the function  x² . And this derivative is equal to the function  2x ,  that is to say the result of the action of the operator  d/dx  on the function  x²  is another function, namely  2x.  Some functions, however, behave in a peculiar way when subjected to this operator (d/dx). For example the derivative (to x) of the function  e^3x is equal to  3e^3x .  In this case we see that the original function  e^3x is recovered, but now multiplied by a certain number, which is in the present case the number  3 .
Functions, that, after being subjected to a certain operator, return in their original form, are called  eigenfunctions of that operator, and the numbers with which those eigenfunctions turn out to be multiplied are called the  eigen values of the operator. So with each operator is associated a set of numbers (a set of numbers, because the operator can act on several different functions resulting in different numbers to appear). This set forms the  spectrum  of the operator. This spectrum can be discrete when the eigenvalues form a discrete sequence (like the set of natural numbers, 0, 1, 2, 3, ...), or continuous when those eigenvalues form a continuous sequence (like a set of real numbers, for instance all those between 0 and 1). So we now have a mathematical formalism that expresses observable quantities and their possible values :  The possible results of measuring such a quantity ('observable') are just the set of eigenvalues of the corresponding operator (which stands for that particular observable). If those operators really stand for observables, then their eigenvalues must be real numbers (which include natural numbers), and not, say, complex numbers (which contain the notorious square root of minus one, and which play, elsewhere in the quantum formalism an important role). Well, if we restrict ourselves to so-called hermitean operators, then it is guaranteed that their eigenvalues are real numbers and thus can represent sensible results of measurements (which are always expressed as a certain number, times some appropriate unit, for example '12.344 millimetres, where 12.344 is a real number). Moreover, the operator must be linear, which means that it transforms sums into sums and multiples into multiples. Formally, the operator  O  is linear if, when it turns a state vector (as such representing the state of a system or particle)  V₁  into  V'₁  and  V₂  into  V'₂ ,   then also

V₁ + V₂ becomes V'₁ + V'₂ ,  and

nV₁ becomes nV'₁ ,  where  n  is some number.

By no means all operators are linear however. The operation of squaring numbers is a counter example. It turns 1 into 1,  2 into 4, but since it turns 1 + 2 = 3 into 9, we see that this is not equal to 1 + 4.
The linearity of operators to be used in quantum theory is a necessary condition, because otherwise the phenomenon of superposition could not be expressed.
In quantum theory an eigenfunction stands for a definite state of say an electron. It is expressed as a state vector in some abstract vector space. We are now able to understand why our information about the states of motion (state vectors) of, say, an electron, is so restricted in quantum theory. If we could know both where a particle was and also what it was doing, it would then have to be in a state which was simultaneously an eigenstate of the position operator  x  and also an eigenstate of the momentum operator  p . The mathematicians tell us that this would only be possible if the operators  x  and  p  were to commute, which means that when they are multiplied together in a given order (i.e. applied one after the other) they must give the same result as when they are multiplied in the reverse order, just like in our ordinary arithmetics 2x3 = 3x2 = 6. However, for operators this is not usually the case. In quantum theory it turns out that the operators  x  and  p  do not commute, which is why there cannot be a state in which they both take definite values. This is Heisenberg's celebrated principle of uncertainty for the quantities position and momentum (which reveals itself strongly only in the quantum mechanical domain of the microworld). Now quantum mechanics says that the Schrödinger wave equation describes a smooth and determined development of states of, say, an electron as it goes about its business, as long as it not being interfered, especially by an observation. While the electron originally was in a state of superposition of possible values, as soon as it is interrogated by some observational device, it shows one of those superposed values as predicted (only) statistically -- i.e. in terms of chances -- by quantum theory. In the language of operators :  the electron originally was not in an eigenstate of position but in some superposition of such states. After the act of measurement it finds itself in an eigenstate of position (i.e. in an eigenstate of the position operator) corresponding to the eigenvalue which is the result of that particular measurement, and which result was statistically predicted by quantum theory.
Every act of measurement has this character of entailing instant change. Beforehand our system is not in general in an eigenstate of the observable (i.e. of the observable quantity under discussion) we are intended to measure, but rather it is a superposition of such states. Afterwards the system is in that particular eigenstate, selected from the original superposition, which corresponds to the eigenvalue actually obtained as the result of that measurement. This discontinuous change is called the collapse of the wavefunction. The idea is that the probability, which was originally spread out in a wavefunction covering the particle being 'here', 'there' and perhaps 'everywhere, is now all concentrated 'here'. It has collapsed onto itself.
Now BOHM maintains that quantum theory all by itself does not describe time and consequently not the phenomenon of process. To remedy this, can be done by the extension of quantum theory with the concept of implicate order. Between the Explicate Order (the world of material objects) and the Implicate Order there is a dynamics going on of projection and injection like we saw it in the analogy of the ink-in-glycerine model, described in the second document of the present website. There we saw the ink-droplets becoming implicate (enfolded) -- which is injection -- and explicate again (unfolded) -- which is projection. This process of injection and projection goes on and on, so we must speak of re-injection and re-projection.
We have a re-projection of some aspect of the multi-dimensional Whole onto our three dimensional Explicate Order (represented by the becoming explicate of an ink droplet) which constitutes a moment, and that moment is a movement, namely the ('vertical') explication movement. And then we have a re-injection, namely the ('vertical') implication movement. And this goes on and on, constituting a time sequence of events. Re-injection is exactly what the Schrödinger equation is describing, and as such it describes the state of superposition of possible values of the quantity under investigation. And re-projection is the next step, which quantum mechanics doesn't handle, except by the arbitrary assumption that the wave function (representing the state of superposition) 'collapses' in a way that has no place in the physical laws, such as Schrödinger's equation, because the latter describes continuous change while it is resulting in a discontinuous change from a state of superposition to a state of definite value, i.e. from a superposition of eigenstates to one eigenstate (eigenvector) corresponding to the eigenvalue of the given operator which (value) is the result of that particular measurement.
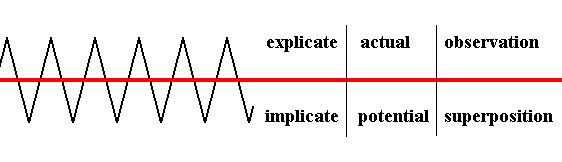
So the quantum system, left to go its own way, is in a state of superposition, which BOHM equates with a state of re-injection and this, in turn, with a state of potentiality. As such it cannot be observed. But because the re-injection is followed by a re-projection (and this in turn by a re-injection, etc.) we can observe almost whenever we want to. We then see the system in its actual states that follow quicly upon each other but always mediated by in-between re-injections. Now, in quantum mechanics, there is no concept of actuality whatsoever, because quantum theory maintains that its equations don't describe anything actual, they merely describe the probability of what an observer could see if he had an instrument of a certain appropriate kind, and this instrument is therefore supposed to be necessary for the actuality of the phenomenon. But the instrument, in turn, is supposed to be made of similar quantum particles as those which it is supposed to observe, obeying the same laws, which would, in turn, require another instrument to give them actuality, and that would result in an infinite regress. So one sees that such an interpretation, as is done in current quantum theory, leads to absurdities. Instead of bringing in time by the assumed collapse of the wavefuntion, BOHM, brings it in as follow (as already hinted at earlier) :  Each moment, which in BOHM's sense is a re-projection or a re-injection, has a certain range of potentials, represented by the Schrödinger equation, and also an actuality, which is more restricted (represented by the particle itself, as a re-projection). And now we say that the next moment has its potential and its actuality (because each projection or injection event involves potentiality as well as actuality), and we must have some connection between the actuality of the previous moment (and in fact moments) and the potentials of the next. That actuality of the past is injected into that field from which the present is going to be projected. And now we can built up a series of actualities injected (alternating with projections) which would narrow down the range of the relevant potentials more and more, and these, i.e. those past actualities, would form the basis of subsequent projections. That would account for the influence of the past on the present. In the Explicate order we see then a more or less causally connected sequence of events, in the form of a recurrent actuality. This recurrent actuality can be observed whenever one wants to. So in BOHM's view the actuality is not caused by the act of observation (measurement). The next diagram illustrates something of the above.

Figure 1.  Moments as projections and injections. Past actualities can influence present potentialities via the Implicate Order.

We will now give a qualitative version of BOHM's hidden variable theory.
This theory proposes that there are (non-local) hidden variables in some sub-quantum level, co-responsible for effects at the quantum level (and with it (sometimes) at the macroscopic level).

e-mail : 

back to Introduction

back to the Ink-in-Glycerine Model

back to Part I of The Crystallization process and the Implicate Order

back to Part II of The Crystallization process and the Implicate Order

back to Part III of The Crystallization process and the Implicate Order

back to Part IV of The Crystallization process and the Implicate Order

back to Part V of The Crystallization process and the Implicate Order

back to Part VI of The Crystallization process and the Implicate Order

back to Part VII of The Crystallization process and the Implicate Order

back to Part VIII of The Crystallization process and the Implicate Order

back to Part IX of The Crystallization process and the Implicate Order

back to Part X of The Crystallization process and the Implicate Order

back to Part XI of The Crystallization process and the Implicate Order

back to Part XII of The Crystallization process and the Implicate Order

back to Part XIII of The Crystallization process and the Implicate Order

back to Part XIV of The Crystallization process and the Implicate Order

back to Part XV of The Crystallization process and the Implicate Order

back to Part XVI of The Crystallization process and the Implicate Order

back to Part XVII of The Crystallization process and the Implicate Order

back to Part XVIII of The Crystallization process and the Implicate Order

back to Part XIX of The Crystallization process and the Implicate Order