In order to apprehend the following discussion about the crystallization process, we begin with stating succinctly the general conclusion, as given in the previous document, about how to visualize the crystallization process in terms of the Theory of the Implicate Order :

1. Because of supersaturation of a solution, or because of a decrease in temperature in a melt, the system of chemical units becomes unstable.

2. Quantum mechanics prescribes how a stable situation (stable arrangement of chemical units) must look like.

3. The potential field of the ordinary forces can now going to become actual, in virtue of the instability.

4. The ordinary (explicate) relatively strong forces, coming from, and acting on, the chemical units, are now being modulated by the much weaker, though more subtle, forces of the activated group theoretic formative field, resulting in the actual attainment of the stable end destination of the chemical units. This stable destination is the (periodic) arrangement of the chemical units according to the appropriate lattice, such that the symmetries, associated with the activated Group (as field aspect present in the Implicate Order), are satisfied.

5. The situation of point 4, is such that it demands to be described in a number of alternative ways, in order to fully express its subtlety and complexity.

6. In crystal formation, the action of the formative field is often such that it allows for a conventional chemical description to be a good approximation, except in observed cases of "cooperation".

7. Group Theory, at least insofar as it deals with the symmetry groups concerning the symmetries of three-dimensional crystals (and also the basic stereometric forms of organisms), can be seen as an aspect of the metaphysical generative order of those crystals (and organisms). It is at the same time an aspect of Nous (Objective Intelligence), the Second Hypostasis of the Neoplatonism of the Greek philosopher Plotinus (third century). And Nous can be identified with an aspect of, or the whole of, the Implicate Order(s). The latter is carried by the Holomovement as its modulation, and this undefinable and unmeasurable Holomovement can be identified with The One, being the First Hypostasis of the Neoplatonism of Plotinus.
   The One is the ultimate creative source of all there is.

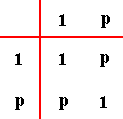
The two group elements, represented by  "1"  (identity element) and  "p" ,  are indicated along the left margin and again along the top margin. The rest of the table indicates how the elements combine. As we can see :  p² = 1. So the period of the abstract element  p  is  2 ,  and any substitution (interpretation) of it by a concrete element (for example, a definite symmetry transformation) having period 2, will preserve the structure of the group table.
Now, if the abstract element  p  were interpreted as representing a rotation of 180⁰ (period 2), then this abstract group is realized as the crystallographic point group  2 .  If, on the other hand,  p  were interpreted as representing a reflection (in a line)(period 2), then the abstract group is realized as the crystallographic point group  m .
These two point groups can be represented by two different motifs (as patterns in their own right), different with respect to symmetry.

Our 2-D periodic pattern, consisting of 2-fold motifs (each of them representing the Point Group 2), placed in an oblique lattice (net), belongs to the Plane Group P2.  In addition to 2-fold rotations, this Group also contains two types of translations, forbidding it to be a point group. The period of any translation is equal to infinity, because repeating it will never end up at our starting point, i.e. its continued repetition generates ever more new group elements.
The next Figure depicts a version of a pattern (which can represent a 2-D crystal) according to the Plane Group P2 .

Figure 1.  Periodic pattern of motifs according to the Plane group P2 .
Each motif s.str. consists of two asymmetric motif units (commas). The motif s.l. (i.e. the motif in the broad sense, thus (also) including the appropriate part of the homogeneous background) is indicated.
The motifs are arranged according to an oblique point lattice (net). The points of intersection of the lines are the nodes of the net. Each node signifies a same environment within the pattern, i.e. those points indicate equivalent sites of the pattern. The lines also outline the parallelogram-shaped unit cell of the pattern, which means that the pattern can be built up by periodically repreating that unit cell in two directions, indicated by the translation vectors, determined by the sides of that unit cell.

Figure 2.  Total symmetry of patterns according to the Plane Group P2 . There are neither mirror lines, nor glide lines present. Small solid ellipses indicate the presence of 2-fold rotation axes.

It is instructive to show the other Plane Groups that, have, like the group P2, motifs whose symmetry group consists of two elements, an identity element and an element of period 2.
These Plane Groups are Pm and Cm ,  both having motifs possessing as their only symmetry element a mirror line.
These latter motifs (with symmetry  m ) are compatible either with a primitive rectangular point lattice prescribing its periodic repetition, resulting in the Plane Group Pm, or with a centered rectangular point lattice, resulting in the Plane Group Cm.
Let's begin with the group Pm  :

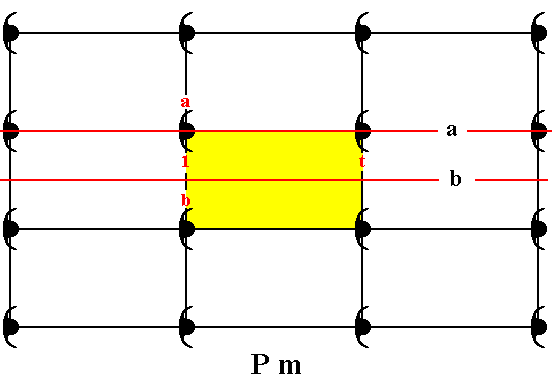
Figure 3.  Placing symmetric motifs in a primitive rectangular lattic, yields a periodic pattern according to the Plane Group  Pm . It has two different types of mirror lines,  one represented by the group element  a , and  another, represented by the group element  b ,  and two types of translation, one horizontal (represented by the group element  t ) and one vertical (represented by yet another group element, not indicated).
The symmetry of each motif s.str. (consisting of two motif units) is according to the point group  m .
The pattern must be imagined to be extended indefinitively in 2-D space.

The total symmetry content of the Plane Group Pm is depicted in the next Figure.

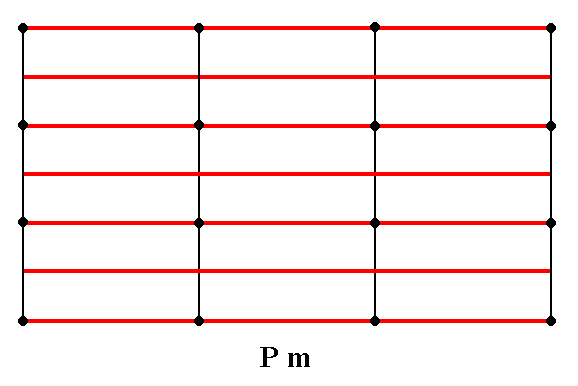
Figure 4. The total symmetry content of the Plane Group Pm.
The only symmetry elements this Group has are mirror lines parallel to the y direction. They are indicated by red lines.
For clarity the nodes of the lattice are indicated (black dots).

Figure 5.  Placing symmetric motifs in a centered rectangular net, such that each lattice node is associated with such a motif, yields a pattern representing Plane Group Cm.  The pattern must be conceived as extending indefinitely in two-dimensional space.

The total symmetry content of the Plane Group Cm is shown in the next Figure.

Figure 6. Total symmetry content of the Plane Group Cm.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by red solid lines.
All the glide lines and mirror lines are parallel to the y direction.
For clarity the nodes of the net are indicated (black dots).

In Figure 7 a possible oblique net is drawn (notice that the drawing is not meant to be a perspectivic one. All angles are real angles).

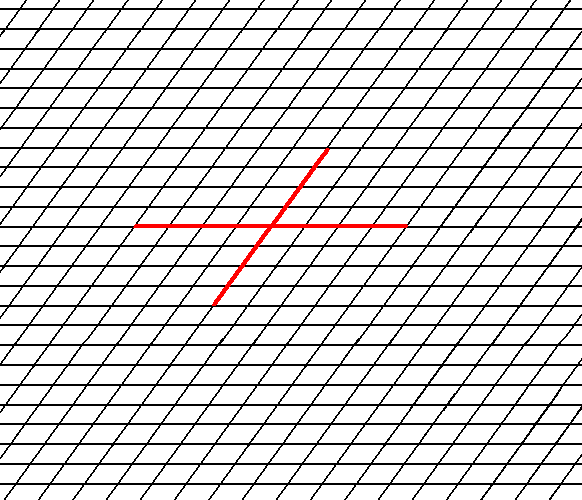
Figure 7.  A possible oblique net (2-D lattice). Two symmetry types of motifs can be periodically repeated according to this net. The possible symmetry types of the motifs are represented by the Point Groups 2 and 1, which means that only motifs having a symmetry of  2  (which is one particular realization of the abstract point group C₂ ), or motifs having symmetry 1 (which means having no symmetry at all), can be compatible with such a net. Inserting a higher symmetric motif in that net (i.e. in an oblique net) results in the net destroying that motif's symmetry and transforming it to (it then having) the point symmetry of the net, which is  2 .
As indicated, a set of crystallographic axes can be based on this net.

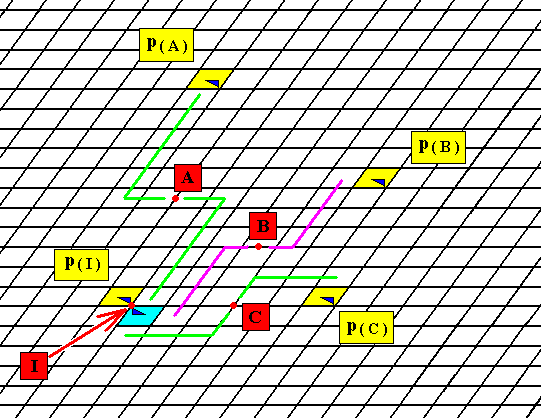
Figure 8.  A  P2  pattern demands the presence of a 2-fold rotation axis at every corner of (each) mesh, and in addition, also at the center of (each) mesh and at te center of its sides. A few such axes are indicated, I, A, B, C.
As  initial  (asymmetric) motif unit we have chosen the one that lies in the blue mesh. The two-fold axis  I  at the upper left corner of that mesh, creates an image of the initial motif unit, and this image is  p(I) . Here the group element  p(I)  is represented by the motif unit  p(I) , and is generated by applying the symmetry transformation  p(I) ,  which is a rotation of 180⁰ about the axis  I ,  to the initial motif unit (initial group element).
In the same way the motif  p(A) ,  representing the group element  p(A) ,  is generated by applying the symmetry transformation  p(A) ,  which is a rotation of 180⁰ about the axis  A ,  to the initial motif unit.
Further, the motif unit  p(B)  is generated by rotationg the initial motif unit 180⁰ about the axis  B .  And the motif unit  p(C)  is obtained by rotating the initial motif unit 180⁰ about the axis  C.
All those 2-fold rotation axes represent different group elements. Although they all are half-turns and so all of the same period, namely 2, their axes of rotation are different, i.e. those axes lie in different locations. And because we must consider the pattern to extend indefinitely, every half-turn about such an axis will leave the whole structure unchanged, i.e. the whole structure, including its details, occupies the same space as it did before the rotation had taken place. Thus these axes really represent  s y m m e t r i e s  of the pattern.
When all the motif units are generated, we will see a 2-fold motif, consisting of two asymmetric motif units, at each node of the lattice, as in Figure 1. One such 2-fold motif we already see in the present Figure at the axis  I .

Figure 9.  Motifs s.l.  (the blue and red parallelograms) arranged according to the Oblique 2-D point lattice, and as such representing the  P2  pattern of Figure 1.
The red parallelograms and the blue parallelograms (both representing motifs s.l.) are wholly equivalent. At every node of the point lattice there is such a motif s.l.

Figure 10.  Each motif s.l.  represents two group elements. These group elements are indicated by the red and blue triangles (The different colors do not represent any qualitative difference). One such half motif s.l. is chosen as the initial group element, denoted by  1,  from which the whole pattern can be considered to be constructed by applying to it three generator elements.

Figure 10a.  One group element from the pattern of Figure 10. Each group element is represented by half a motif s.l., and thus by one motif s.l. unit (One motif s.l. consists of two units).

Figure 11.  Three generators are indicated. The rotation  a  is about the point indicated (yellow). Let us call this point  R.
These generators are at the same time group elements. From the initial group element  1  all the other group elements can be generated by applying to it, and to the results, the generators.

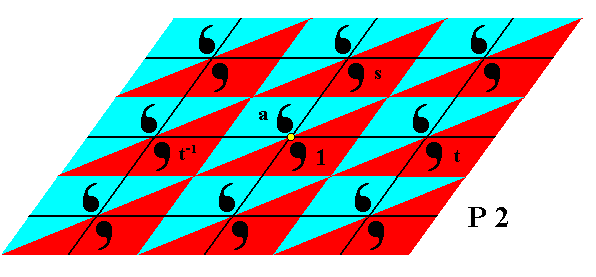
Figure 12.  The group element  t^-1  is generated from the element  1  by applying the inverse of the generator  t .

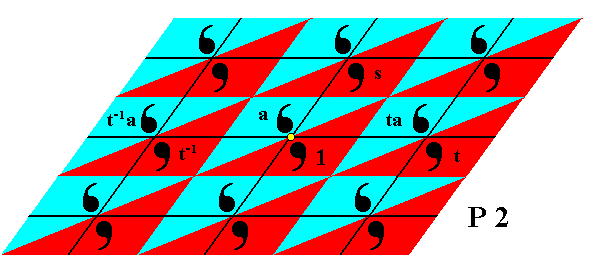
Figure 13.  The group elements  t^-1a  and  ta  are generated from the element  a , by applying  t^-1 and  t  respectively.

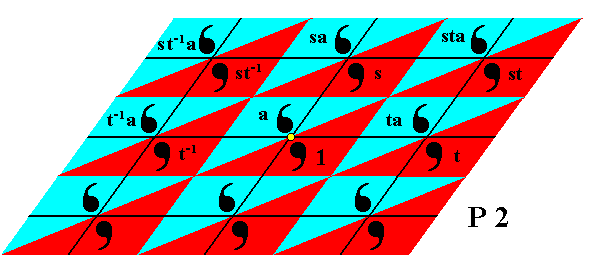
Figure 14.  Further group elements are generated by applying the generator  s  to earlier generated elements.

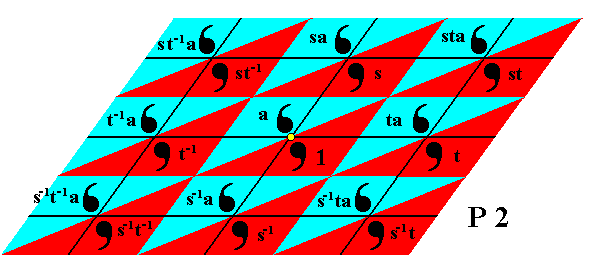
Figure 15.  Still further group elements are generated by applying the generator  s^-1  to earlier generated elements.

The order in which we generate the elements can be different from the one we used above. The result will be, however, totally equivalent. So, when, say, we have generated the element  s^-1ta ,  we can subject it to the generator  a ,  which means rotating it 180⁰ about the point R (the yellow point in the Figure). We then get the element  as^-1ta ,  which we had already found earlier as  "st^-1"  (as we can check in the above Figure),  so we now know that  as^-1ta = st^-1 .

In the previous document we have seen that the group elements are abstract in the sense that their boundaries do not necessarily coincide with those of chemical units. The set of group elements (forming a certain Group) only represents the symmetries involved.

Also in that previous document we interpreted the crystallization process in terms of the Theory of the Implicate Order. However, such an interpretation is always incomplete and, moreover, in some way or another wrong. This is because we always have to do with the Whole (i.e. the Whole is always involved in whatever we are investigating). Whatever is said about something specific, it is in fact always said about the Whole. And whatever we say, or find out, about the Whole, there is always something more and something different. And this implies that when we try to describe a certain phenomenon in the Explicate Order -- in our case the crystallization process -- we must use a plurality of descriptions, while, for the time being, tolerating apparent contradictions between them. We must realize that we are engaged in an ongoing process of understanding how things are and behave, as just aspects of the Whole.
Metaphysically, the Theory of the Implicate Order can be placed into the Neoplatonic framework of the descend (and return) of metaphysical levels, devised by the third century Greek philosopher PLOTINUS. As in the Theory of the Implicate Order, in Neoplatonism it is such that if we go down to the fundamentals (i.e. if we go from the material world all the way to "The One", as the origin of all of Reality), things are not becoming ever more simple (in the sense of some ultimate particles or ultimate fields for that matter), but, on the contrary, they become more complex (but at the same time more unified), and especially ever more subtle, ending up at an infinite richness, without any limits and totally undefinable, which implies that we can never arrive at some sort of fundamental and ultimate 'Theory of Everything' aspired by modern physics and cosmology.
The undefinable and unmeasurable holomovement (carrying, as its modulation, a series of implicate generative orders) can be related to Plotinus' The One, which is pure Unity, and the highest of the three "hypostases", which all are immaterial metaphysical levels of Reality. From The One an "emanation" takes place, resulting in the two other hypostases, and finally in material things. The latter emanation stage takes place by the reception of the immaterial structures into Prime Matter (About the latter, see the philosophical documents in the First Part of the website, accessible by the BACK TO HOMEPAGE link at the end of the present document.). Because of this emanation the unity of the world is guaranteed, there is no unbridgable gap between the material and immaterial domains. The material domain of Neoplatonism can, in a way, be identified with BOHM's Explicate Order. Matter, according to Plotinus, is not an independently existing principle, but the point at which the outflow of reality from The One fades away into utter darkness. Along with the emanation from The One, an increasing  fragmentation  takes place, culminating in the high degree of separateness of objects and processes in the Explicate Order. Hence at each stage of this emanation the descent into greater multiplicity imposes fresh limits and restrictions, disperses and weakens the power of previous stages, and creates fresh needs requiring the development of new faculties previously unnecessary.
The Second Hypostasis, Intelligence (Nous), as such emanating from The One (the First Hypostasis), represents the first stage of fragmentation :  Although its (intelligible) contents are not separated from each other, they are clearly distinguished. It is a unity-in-plurality, a multiple organism containing a plurality of Forms. These Forms are contemplated or thought by Intelligence, in such a way that there is no distinction between subject and object. Intelligence is identical to its contents, i.e. it has a sort of self-awareness. The Forms are the immaterial objective structures, which I identify with objective mathematical structures.
The Third Hypostasis, Soul (Psychè), brings about a still further fragmentation :  The perfect self-awareness of Intelligence, based on full identity between subject and object, is impossible on the level of Soul. A corollary is that Soul's contemplation is confined to mere images reflecting the Forms, whereas the objects contemplated by Intelligence are the Forms themselves. The Second and Third Hypostases could be identified with BOHM's hierarchy of implicate generative orders.
In a certain sense The One is not. It just creates Being. In another sense Prime Matter is not, because it is pure potentiality, and needs form to be able to exist actually.
Matter receives this form. as intelligible content, from Soul, and indirectly from Intelligence, and ultimately from The One. In this way the observational material world comes into being, and this world can -- as has been said -- be identified with BOHM's Explicate Order.
In terms of the implicate orders we can further characterize the three hypostases as follows :

The One is the ultimate implicate order.
Nous is the explicate order with respect to The One.
Soul (i.e. the World-Soul) is the explicate order with respect to Nous.
Nous is the implicate order with respect to Soul.
Soul is the implicate order with respect to the material world.
The material world is the ultimate explicate order. It is the very Explicate Order, totally concrete and individualized.

The sequence from The One down (or up, if one whishes to express it) to the material world is an order of increasing fragmentation.
Soul is the intermediate hypostasis between the intelligible and material worlds.

We will elaborate further on this Neoplatonic metaphysics in a separate document, and will now return to the crystallization process, and place it in this broader philosophical context (i.e. in BOHM's Theory of the Implicate Order, and the Neoplatonic metaphysics).

A crystal, or a developing crystal (or whatever we see in the Explicate Order) is just an aspect of the  W h o l e .  Such an aspect is just a relatively autonomous subtotality. The same holds for the chemical units, involved in crystallization.
But also everything we distinguish within the Implicate Order(s) is just an aspect of that same Whole, a relatively autonomous (implicate) subtotality, which does or does not become explicate.
When something becomes explicate, we have to do with an act that does not consume anything of the Implicate Order(s). The latter is, with respect to its available resources, unaffected by such an act of explication. Such an act is 'undiminished giving', it involves no dissipation of the Implicate Order's power among its products.
With respect to crystallization, the elements of the relevant Symmetry Group (which are symmetry transformations, together having group structure, and reflecting the involved symmetry), are present in the Implicate Order, first of all in a group theoretical abstract sense, but 'after' that, also present therein as being objectively geometrically interpreted, for example as rotations or translations. And this geometric interpretation is just a next stage of emanation (which as a whole extends all the way down to Prime Matter) and, consequently, a further fragmentation (this fragmentation is, however never absolute, but relative). The result of this geometric interpretation is, however, still abstract, but now so in a lesser degree.
When group elements are (objectively) geometrically interpreted, the relative (i.e. mutual) locations, in the Explicate Order, of the chemical units that represent them, are automatically determined.
The generation of the geometrically interpreted group elements (resulting -- in our case -- in a symmetry Group), takes place within the Implicate Order, and is a timeless logical, noetic process (thinking process) of which Soul is its subject, while it is an aspect of the content of Intelligence (where there is no distinction between subject an object). This process (and all other such noetic processes) is constantly recurring, expressing (an aspect of) the (timeless) dynamism of the Third and Second Hypostases and ultimately that of The One (Holomovement), although such a way of speaking is inadequate with respect to The One, because it entails its fragmentation : Within The One there is not only no separation, but also not any distinction. And this is not because The One lacks anything. It stands above all distinctions.
Because of the mentioned noetic process of generating group elements, taking place within the Implicate Oder, the  d e s c r i p t i v e   o r d e r  of Group Theory, especially when concerned with Symmetry Groups, becomes (also) an  o n t o l o g i c a l   o r d e r.
Explication (i.e. unfoldment into the Explicate Order) of a crystal structure according to the noetic generation of geometrically interpreted group elements, necessarily implies an additional interpretation, that is to say a chemical interpretation of those group elements, and now the abstractness is transformed into full concreteness. But still all this remains 'abstract' in the (other) sense that it is just an aspect of the Whole, i.e. a relatively autonomous subtotality, which is in spite of that totally integrated into the Whole. The possibility of such an abstraction from the Whole is rooted in the laws of the Whole (holonomy). The explication process can metaphysically be described as the reception of the noetic precursors of chemical units and their symmetric relationships to each other, into Prime Matter, the ultimate substrate.

Above we described, as an example, the case of crystallization according to the Plane Group P2 (of imaginary two-dimensional crystals).
The generation of the objectively geometrically interpreted group elements, takes, as has been said, place within the Implicate Order (or, as one may say, within Intelligence, and then contemplated by Soul), and as such we can see it as an aspect of a dynamic formative field with respect to crystal formation.
Now as soon as, in the Explicate Order, a solution or melt becomes unstable with respect to a certain chemical substance that could cystallize from such a melt or solution, the appropriate formative field is activated by some non-local resonance phenomenon, and the weak energy of that field directs (i.e. modulates) the higher energies of the system of the relevant chemical units, such that they arrange in the particular minimum-energy configuration, resulting in a periodic structure with a symmetry according to the relevant Symmetry Group.
What we see in the Explicate Order is the onset of a dynamical process, resulting in crystal formation.
While investigating such a process we sometimes are forced to conclude that some sort of cooperation (discussed in the previous document) must be at work between the chemical units, which behave as a whole. This cooperation (long-range cooperation with respect to the microscopic effective range of the forces at work there) then is an indication of the presence of a directing formative field. When no cooperation is evident in such a process, we theorize that also in this case, but now not directly evident, a formative field is nevertheless involved. In that case a purely mechanical chemical explanation yields a (very) good approximation to what really happens.
As we see, here we have, in explaining cooperation, not brought in the model of projection and injection (according to the ink-in-glycerine analogy of BOHM), but have instead brought in an explanation and interpretation largely according to SHELDRAKE's hypothesis of formative causation, which is very close to the theory of the implicate order of BOHM. This illustrates the fact, as stated earlier, that we must approach the theory of Wholeness from several more or less different viewpoints. These different approaches should, in some way, complement each other.

The next Figure shows the generation of the group elements of the group P1.
The motif s.str.  is an asymmetric Figure (comma), i.e. a figure with point symmetry 1, which means that its only symmetry element is a 1-fold rotation axis, which in turn means that the figure will only occupy the same patch of space when either rotated 0⁰, or 360⁰, or an integer multiple of 360⁰. And this is equivalent with having no symmetry at all.
The motif s.l.,  i.e. the comma plus its corresponding background, has the shape of a parallelogram, just like in the case of the group P2. But we see that the parallelogram representing the motif s.l. corresponds directly with a group element.
From a given group element 1, all the other group elements can be generated by applying two generator elements (as all group elements they are symmetry transformations). These two generators are the translations  t  (horizontal translation) and  s  (oblique translation). When applied to the element 1 and to the results thereof, we will generate all group elements, and with it the Group itself, and when indeed the group elements are represented by motifs, we obtain the (whole) pattern.

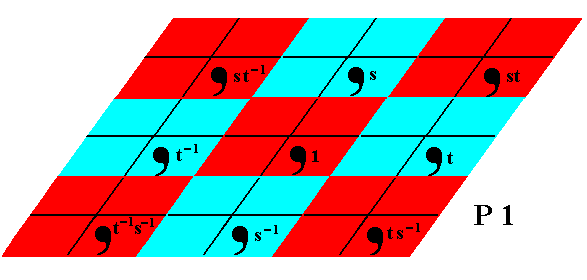
Figure 16.  A  2-D periodic pattern according to the Plane Group  P1  can be generated from an initial group element by applying two translations  t  and  s .
The blue and red parallelograms represent motifs s.l. and at the same time group elements (The colors red and blue do not signify any qualitative difference).

The next Figures show the generation of the group elements of the Plane Group Pm . First we show the motifs s.l.

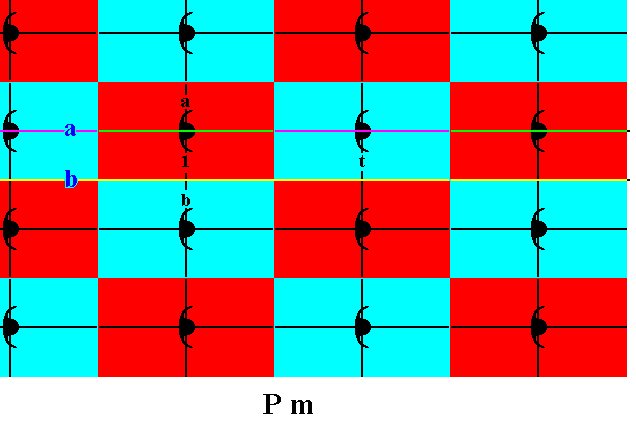
Figure 17.  A  periodic 2-D pattern according to the Plane Group  Pm . The red and blue rectangular areas indicate the motifs s.l. of the pattern. Each motif s.str. consists of two partly overlapping commas, which are the motif units s.str. The motif unit s.str. representing the (chosen) initial group element is indicated (1) , so also the three motif units s.str.,  a ,  b ,  and  t ,  representing the three generators, namely a mirror reflection in the (horizontal) line  a ,  a mirror reflection in the (horizontal) line  b ,  and a horizontal translation  t . (The colors red and blue do not signify any qualitative difference).

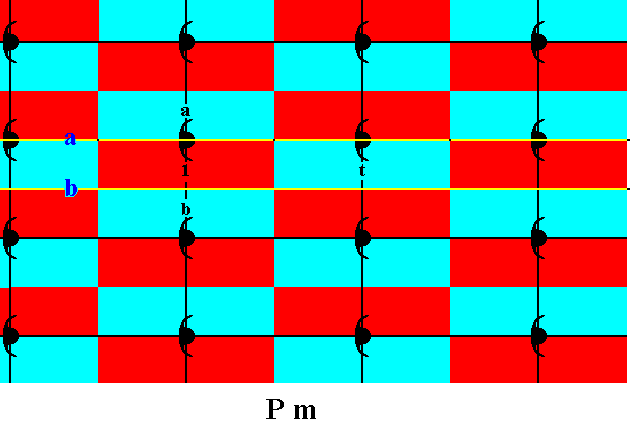
Figure 18.  Each motif s.l. consists of two motif units s.l., and these delimit the group elements (indicated by red and blue slender rectangles). Four group elements are specifically indicated :  One representing the initial element  1 ,  another, representing the mirror reflection  a ,  which is chosen as the first (of three) generator,  a further one representing the mirror reflection  b ,  as second generator,  and finally one that represents a horizontal translation  t , the third generator. (The colors red and blue do not signify any qualitative difference).

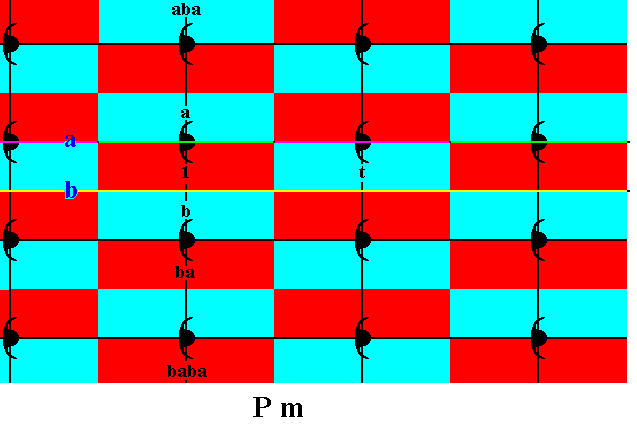
Figure 19.  Generation of group elements of the Group Pm , by means of two parallel mirror lines and (later) a horizontal translation.
The group element  ba  is generated by reflecting the element  a  in the mirror line  b .
The group element  aba  is generated by reflecting the element  ba  in the mirror line  a .
The group element  baba  is generated by reflecting the element  aba  in the mirror line  b .

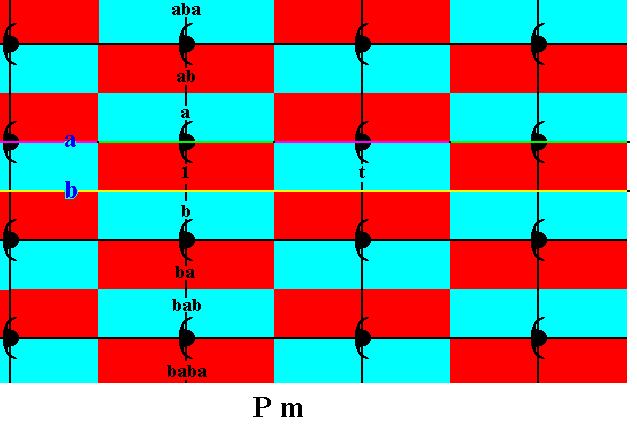
Figure 20.  The group element  ab  is generated by applying a reflection in the line  a  to the element  b .
The group element  bab  is generated by applying a reflection in the line  b  to the element  ab .

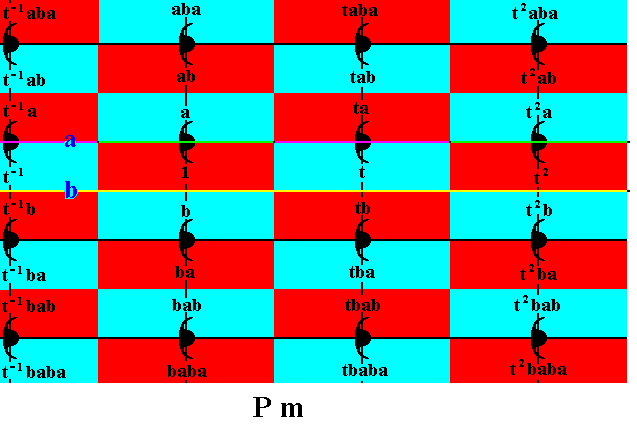
Figure 21.  Generation of the remaining group elements (with regard to the visible part of the pattern) of the Group  Pm ,  by applying the generator  t .

On the centered rectangular point lattice can be based two-dimensional patterns according to the Plane Group Cm , (See Figure 5, and for the pattern of its symmetry elements, Figure 6).
Its motifs have the same symmetry as those of the group Pm , but now such a motif is also present at the center of each mesh.
Also here we will generate the group elements, by applying some generator elements to an initial element.

The next Figure shows a set of two chosen generators :
The element  g  (represented by the corresponding motif unit), which results from the chosen initial motif unit  1  (representing the identity element), by (the action of) the glide reflection  g .
The element  m  (represented by the corresponding motif unit), which results from the initial motif unit (representing the identity element), by a reflection in the line  m .
Recall that a glide reflection is a reflection in some line immediately followed by a translation parallel to that line.

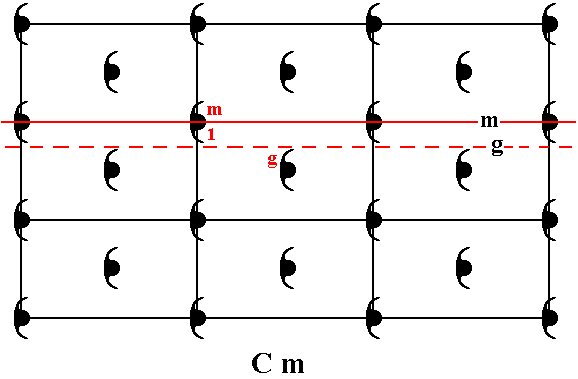
Figure 22.  The two chosen generators of the group  Cm .

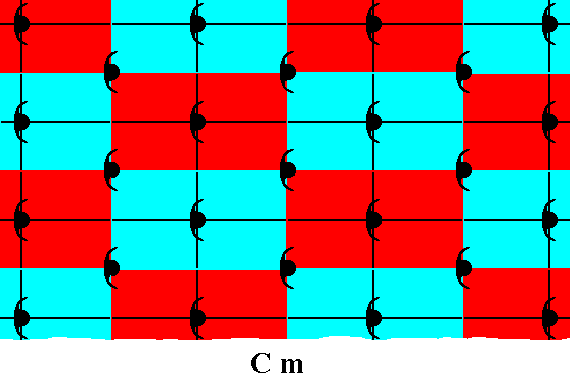
Figure 23.  This Figure, and the next one, show that the motifs s.l. proposed here are false. The point lattice, underlying  Cm  patterns, contains, in addition to the nodes at the corners of the meshes, a node in the center of each mesh. And nodes should indicate equivalent areas of the pattern. We can clearly see that in the case of the present Figure this demand is not satisfied. The next Figure shows this even more clearly. (The colors red and blue in the present Figure do not signify qualitative differences)

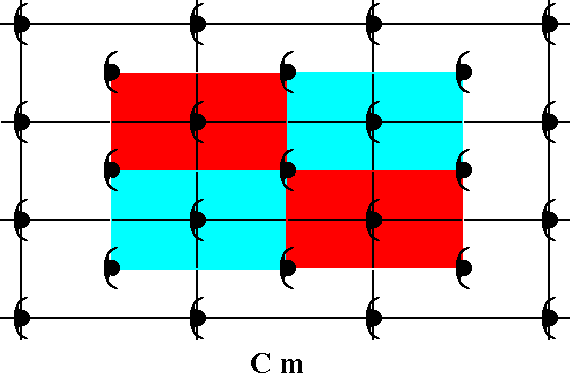
Figure 24.  Associated with each corner node there is a motif s.l., but the node in the center of the mesh is not associated with such a motif. So the proposed motif s.l. is incorrect. (The colors red and blue do not signify qualitative differences).

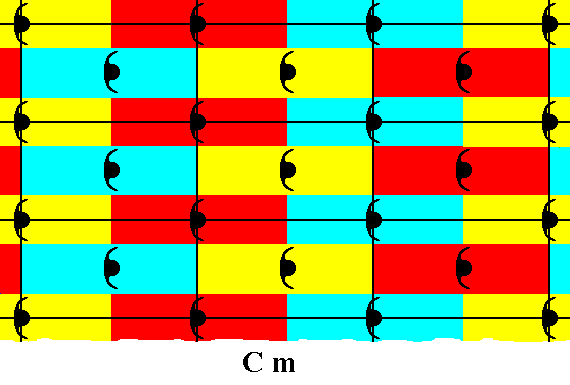
Figure 25.  Correct choice of the motif s.l.  for a  Cm  pattern.
With respect to the present representative of a  Cm  pattern, each motif s.l. consists of one whole motif  s.str.  (itself consisting of two, partially overlapping motif units (s.str.), which in the present case are commas), PLUS an elongated rectangular background area. (The colors red, blue and yellow, do not signify qualitative differences)

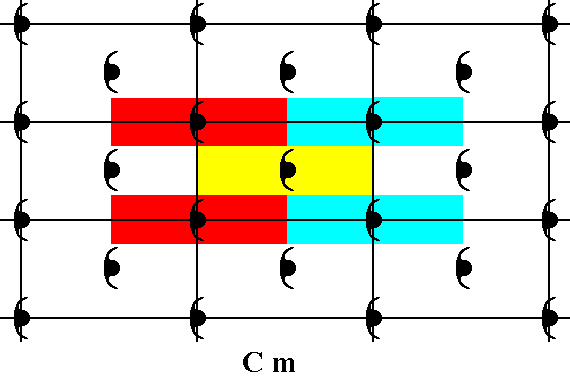
Figure 26.  Each node of the point lattice for  Cm  patterns (which is a centered rectangular point net) is associated with a -- in the previous Figure -- chosen motif s.l. (five are explicitly shown), and thus those nodes indicate equivalent areas of the pattern. (The colors red, blue and yellow, do not signify qualitative differences.)

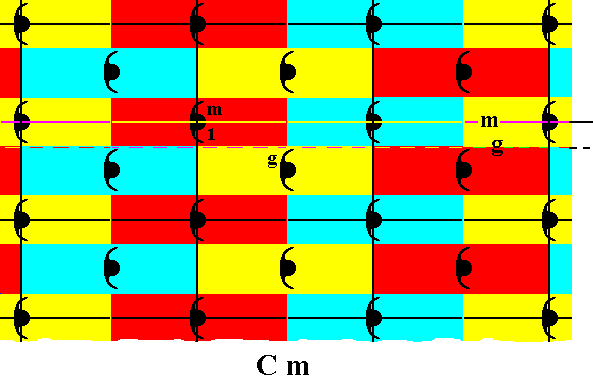
Figure 27.  Motifs s.l. ,  initial element, and generator elements, for a pattern according to the Plane Group  Cm .
The marked group elements are :
The element  g  (represented by the corresponding motif unit), which results from the chosen initial motif unit  1  (representing the identity element), by (the action of) the glide reflection  g  (The corresponding glide line -- as symmetry element -- is indicated by a horizontal dashed line).
The element  m  (represented by the corresponding motif unit), which results from the initial motif unit (representing the identity element), by a reflection in the line  m  (The corresponding mirror line -- as symmetry element -- is indicated by a horizontal line, and coincides with the upper edges of a row of meshes).
The colors red, blue and yellow, do not reflect qualitatice differences.
Recall that a  glide reflection  is a reflection in some line immediately followed by a translation parallel to that line.

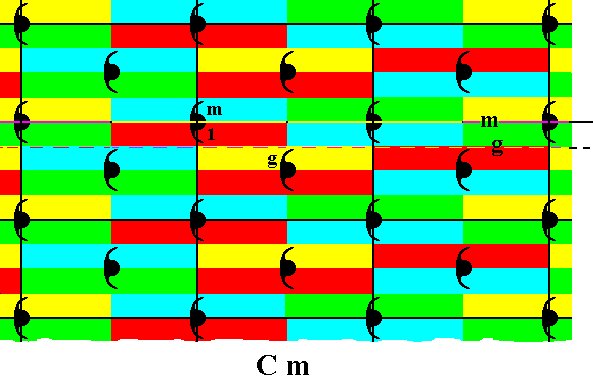
Figure 28.  Each motif s.l. (See Figure 27) represents two group elements. Each such group element is represented by one motif unit of a motif s.str. , i.e. by half a motif s.str. , PLUS corresponding background ( = elongated rectangular area).
( The different colors of the rectangles do not reflect a qualitative diference).

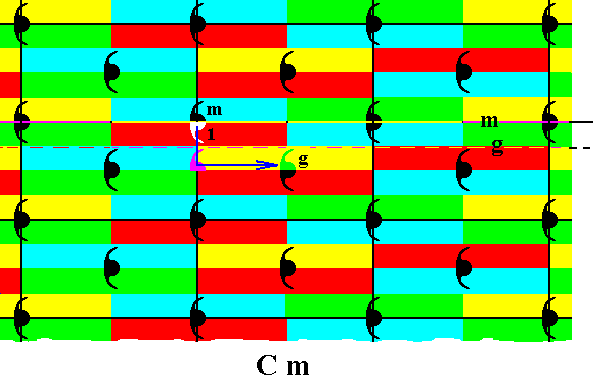
Figure 29.  The same as previous Figure, but now with the glide operation (glide reflection)  g  indicated. See also next Figure (blow-up).

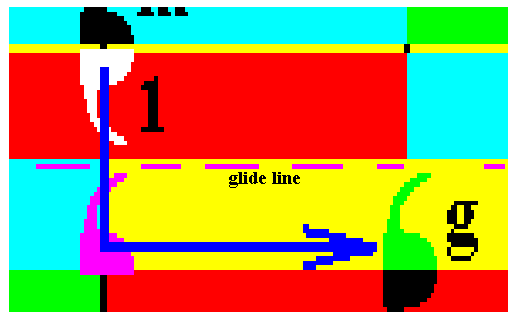
Figure 30.  Blow-up of part of the previous Figure, illustrating the  glide operation  (glide reflection)  g .
A glide reflection is a reflection in a line immediately followed by a translation parallel to that line. In the present Figure we see a motif unit (white) being reflected (purple) in a horizontal line (glide line), and then translated parallel to that line, resulting in the final image (green). So the begin member of this operation (symmetry transformation) is the white motif unit, and the end member is the green motif unit. The glide line is indicated by the dashed line (which is supposed to coincide with the relevant edges of the rectangles).
An infinite pattern possessing such a glide reflection as one of its symmetries, will, after being subjected to such a glide reflection (reflection + translation), occupy the same patch of space, as it did before that operation took place.

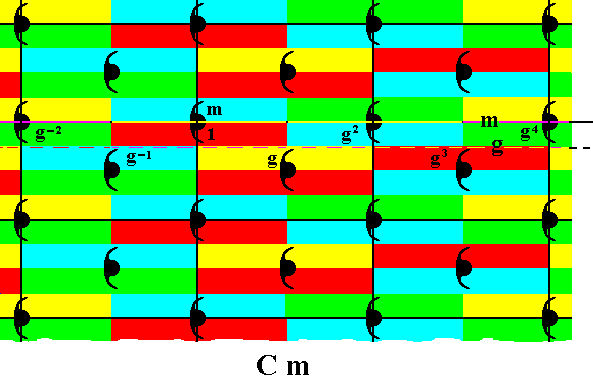
Figure 31.  Generation of the group elements  g^-2, g^-1, g², g³, g⁴ , by (repeatedly) applying the generator  g  to the intitial group element  1 .

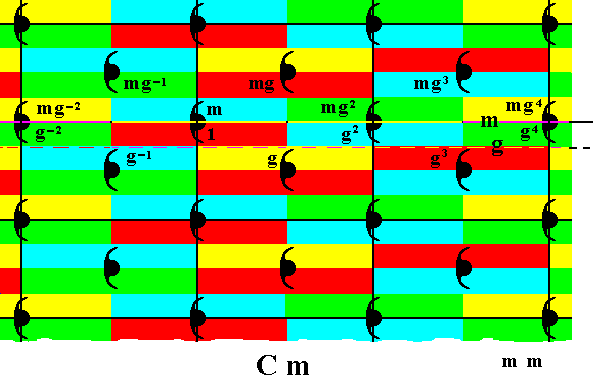
Figure 32.  Generation of the group elements  mg^-2, mg^-1, mg, mg², mg³, mg⁴ , by applyning the reflection  m  to the elements generated earlier.

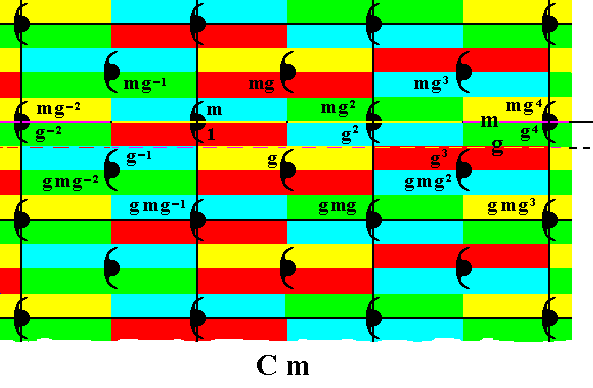
Figure 33.  Generation of the group elements  gmg^-2, gmg^-1, gmg , gmg², gmg³ ,  by applying  g  to earlier generated elements.

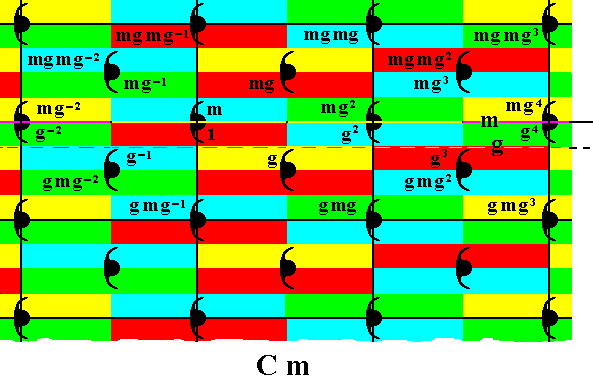
Figure 34.  Generation of the group elements  mgmg^-2, mgmg^-1, mgmg , mgmg², mgmg³ ,  by applying  m  to earlier generated elements.

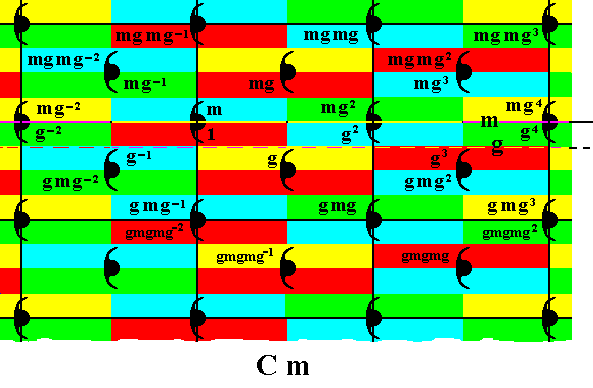
Figure 35.  Generation of the group elements  gmgmg^-2, gmgmg^-1, gmgmg , gmgmg² ,  by applying  g  to earlier generated elements.
Continuing this process yields the (elements of the) Group  Cm .

In the context of the Implicate Order(s) we can again say that the described group theoretic generation process is a dynamic noetic structure (thought structure) within the Implicate Order. This noetic structure is the formative field with respect to the internal symmetry of the developing crystal. The specific nature of the chemical motifs determines a pattern of atomic aspects presented to the growing environment, and that pattern in turn determines a pattern of relative growth rates in specified directions (these directions are determined by the stacking of building blocks). And this pattern of directed relative growth rates determines the intrinsic point symmetry of the developing crystal, i.e. its intrinsic external shape.
In the context of the Neoplatonic metaphysics we can say that the particular Symmetry Group as such is present in the hypostasis of Intelligence in the sense of the latter's intuitive thought, while noetic generation of the Group is present in Soul, the third hypostasis (or third metaphysical level), that is to say, Soul contemplates the Group as a whole, but it can do so only by fragmenting it, because its thinking mode is discursive. This results in the generation of the group elements as logical process, which is as such the 'formative plan' with respect to the internal symmetry of a crystal, as to be finally realized in Matter.
Prime matter, i.e. pure potentiality, being the lowest principle of the whole metaphysical hierarchy, needs a Form in order -- as a matter-form composite -- to exist at all. So matter all by itself does not have form. In this respect it resembles The One, the first hypostasis, which also does not have form, but whereas Matter's negativity consists in total deprivation of all form, The One is on a more exalted level, and in its perfect self-sufficiency has no need of any form.
Every emanation step (i.e. every step in the outflow of Reality (ultimately) from The One), can be seen as follows :  Entities that have achieved perfection of their own being (by contemplating the Forms of the next higher metaphysical level), do not keep that perfection to themselves, but spread it abroad by generating an external 'image' of their internal activity. So from Intelligence to Soul, and from Soul to Matter. In this way Soul conveys form to Prime Matter, i.e. the latter 'expresses' this form under conditions of (still) greater multiplicity and separation, and so revealing it to the external world, which process is described in the Theory of the Implicate Order as explicitation of a relatively autonomous subtotality in the Implicate Order out into the Explicate Order. In Sheldrake's Field Theory it is described as the embedding of an incipient structure in the formative field.

e-mail : 

back to Introduction

back to the Ink-in-Glycerine Model

back to Part I of The Crystallization process and the Implicate Order