We will now investigate the generation of the Plane Group P2mg, i.e. the generation of its group elements.
The Plane Group P2mg
The (primitive) Rectangular Net, which itself has 2mm (point) symmetry, and is consequently compatible with 2mm motifs, can also accommodate for motifs having a lesser degree of point symmetry, provided that their symmetry elements are aligned with the corresponding symmetry elements of the net. Such a motif can either have a point symmetry of 2, i.e. having a 2-fold rotation axis as its only symmetry element, or have a point symmetry of m , i.e. having a mirror line as its only symmetry element. We'll consider the latter type of motif.
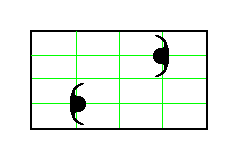
Two such motifs are placed in a mesh of a primitive rectangular net as follows :
Figure 1. Two motifs, each having point symmetry m , are placed in a mesh of a primitive rectangular lattice, as indicated ( The Figure depicts one mesh only. The green lines indicate the exact location of the motifs in such a mesh).
The next Figure depicts a regular periodic pattern of motifs, that have a symmetry m, resulting in the Plane Group P2mg.
Figure 2. If we place two motifs, having a symmertry of m , in each mesh of the primitive net, as indicated in Figure 1, then we will obtain a periodic pattern of motifs representing the Plane Group P2mg.
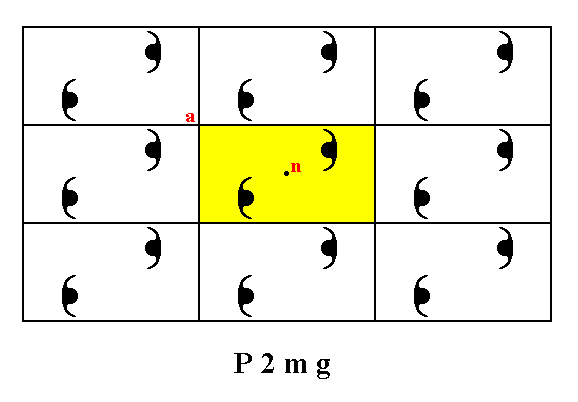
Figure 3. For the pattern of Figure 2 a unit mesh is chosen (yellow). This unit mesh has point symmetry 2, and is primitive (P).
Point n is not equivalent to point a , because the orientations of the motifs bottom-left and top-right to them are different. So indeed the unit mesh is primitive (i.e. if we consider the four corners of the unit mesh as being lattice points, then the point in the center of that mesh -- and also in all other meshes -- is not a lattice point).
The next Figure gives the motif s.str. and the motif s.l. of the pattern of Figure 2. The motif s.l. is repeated indefinitely across the two-dimensional plane.
Figure 4. The motif s.str. (black) and the motif s.l. (black + blue) of the pattern representing Plane Group P2mg . The motif s.l. is indefinitely repeated along the directions of the 2-D lattice.
To determine the translation-free residue (i.e. to determine the point group symmetry) of the pattern representing the Plane Group P2mg, we contract the whole structure together till all translations are zero. The figure (shape, pattern) we end up with is depicted in the next Figure.

Figure 5. Eliminating all translations yields a figure that has a point symmetry 2mm , which represents the translation-free residue of the Plane Group P2mg .
In the pattern, representing the Plane Group P2mg we can detect 2-fold rotation axes, mirror lines and glide lines.
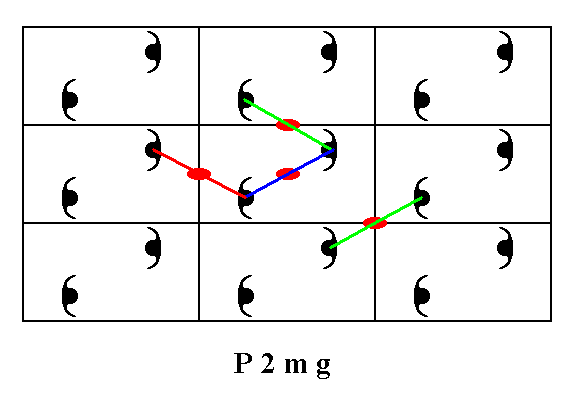
Figure 6. Some of the 2-fold rotation axes, belonging to the symmetry content of the Plane Group P2mg , are indicated. The colored lines serve to show that there indeed are 2-fold rotation axes perpendicular to the plane of the drawing.
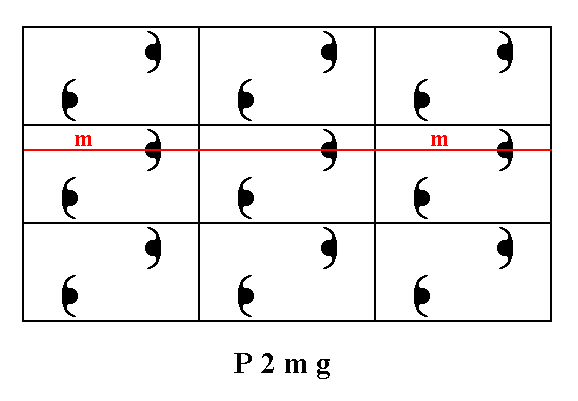
Figure 7. The pattern representing Plane Group P2mg has mirror lines parallel to the y direction. One of them is depicted.
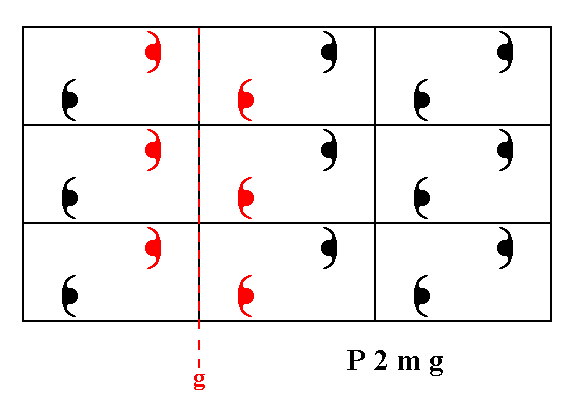
Figure 8. The pattern representing Plane Group P2mg has glide lines parallel to the x direction. One of them is depicted.
The total symmetry content of Plane Group P2mg is given in the next Figure.
Figure 9. Total symmetry content of the Plane Group P2mg .
Solid red lines indicate mirror lines.
Small solid red ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
The glide lines are all parallel to the x direction, some going through the mid-line of the rectangles, others coinciding with their (vertical) sides. They are indicated by red dashed lines.
Generation of the group elements of the Group P2mg
The P2mg pattern, as realized in Figure 2, consists of composed motifs. Each such motif itself consists of two motif units -- partly overlapping commas -- which represent group elements (and each group element is a symmetry transformation of the pattern).
For generating the P2mg pattern, and with it the (elements of the) group P2mg, we choose the following set of generators :
The element g which results from the (chosen) initial motif unit (representing the identity element) 1 as the effect of the glide reflection (glide line) g .
The element m which results from the reflection of the initial motif unit in the mirror line m .
The element t which results from the initial motif unit in virtue of a horizontal translation t . See next Figure.
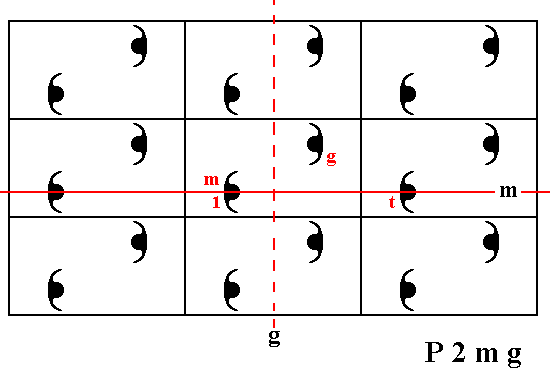
Figure 10. Three generators for the P2mg pattern are indicated.
The next Figure shows how all the group elements can be generated from the three generators g , m and t .
Figure 11. Generation of the P2mg pattern from the three generators.
In accordance with Figure 4 we now tesselate the displayed part of our P2mg pattern with motifs s.l. :
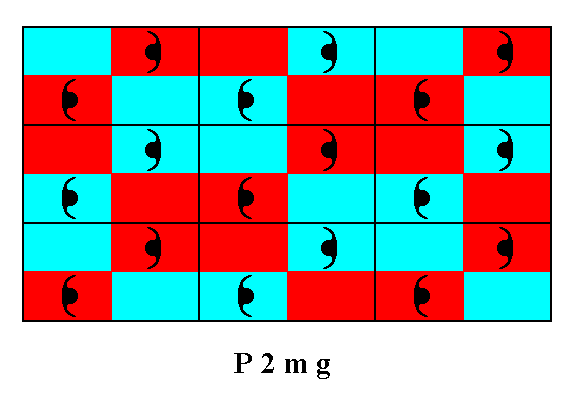
Figure 12. Tiling of the plane with motifs s.l. (red and blue rectangles) of the P2mg pattern of Figure 2.
( The red and blue colors of the motifs s.l. do not indicate qualitative differences).
We can now divide the motifs s.l. into areas which are supposed to represent group elements. The next Figure divides the motifs s.l., but closer inspection reveals that the way of division is not correct. We show it anyway because it is instructive.
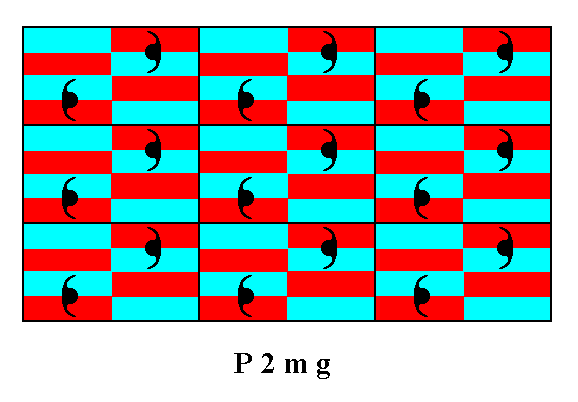
Figure 13. Division of the motifs s.l. in order to obtain areas that represent group elements and tile the plane completely. As one can see, however, the division is not correct : From Figure 11 we can see that each group element is associated with one motif unit, i.e. with one half of a motif s.str. In the present Figure we see subareas (resulting from the division) that contain such a half-motif (s.str.). However, there are also areas (supposed to be equivalent) not containing such a half-motif. So the plane is not divided into tesselating areas, such that each of them represents a group element.
The next Figure shows the correct division of the motifs s.l.
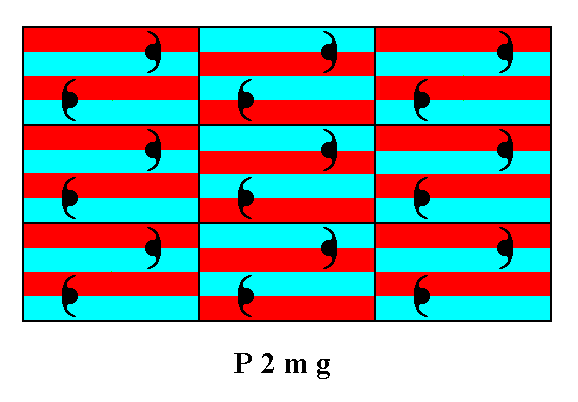
Figure 14. Correct division of the motifs s.l. of Figure 12.
Each resulting subarea (red and blue slender rectangles) contains one half-motif (s.str.), and consequently represents a group element. These subareas also tesselate the plane completely.
The next Figure again shows this division but now with the initial group element 1 and the three generator elements g, m, t indicated, together with the symmetry elements -- glide line and mirror line -- corresponding to g and m .
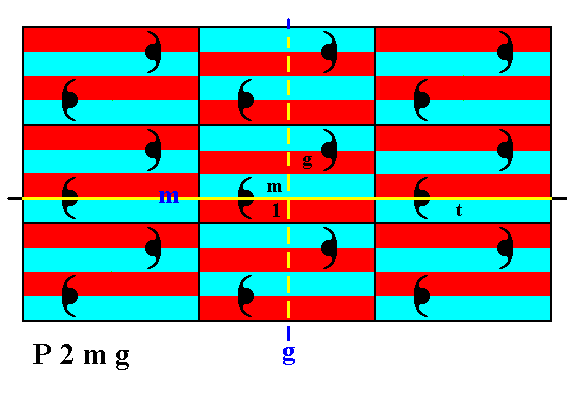
Figure 15. The tiles (red and blue rectangles) of the plane, as indicated in this and the previous Figure, represent (with their shape and content) group elements. Three of the latter are specifically indicated :
The initial group element 1 (identity element).
The group element representing the glide reflection g , with respect to the (dashed) line g , chosen (from an infinity of possible glide reflections -- see Figure 9) as a first generator.
The the group element representing the reflection m , with respect to the mirror line m , chosen (from an infinity of possible mirror reflections -- see Figure 9) as a second generator.
The group element representing a horizontal translation t , which is chosen as a third generator.
(See also Figure 10)
The next Figure shows the generation of some group elements, by (repeatedly) applying the generator g to the initial group element.
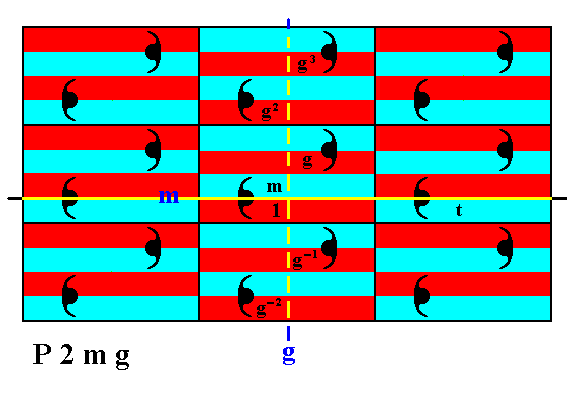
Figure 16. Generation of the group elements g-2 , g-1 , g2 , g3 .
The next Figure shows the generation of some more group elements, by (repeatedly) applying the generator g to the group element m .
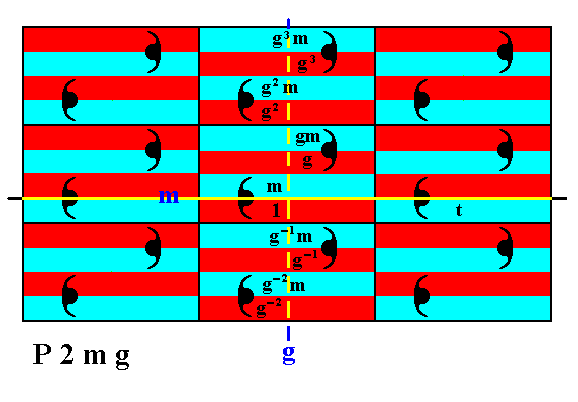
Figure 17. Generation of the group elements g-2m , g-1m , gm , g2m , g3m .
We can now generate all the remaining group elements (as far as the displayed part of the pattern is concerned) by repeatedly applying the horizontal translation t and its inverse t-1 . See next Figure.
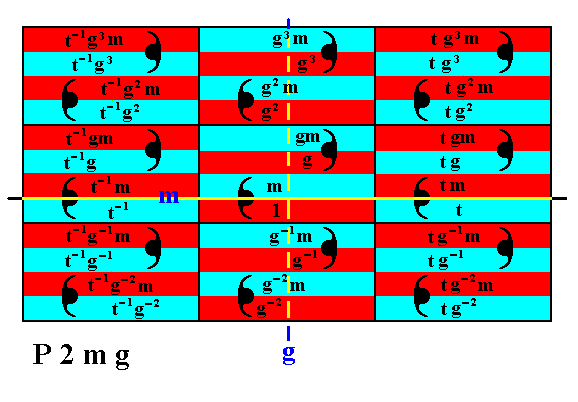
Figure 18. Generation of the group elements t-1 , t-1g-2 , t-1g-1 , t-1g2 , t-1g3 ,
tg-2 ,
tg-1 , tg2 , tg3 ,
t-1g-2m , t-1g-1m , t-1g2m , t-1g3m , tg-2m , tg-1m , tg2m , tg3m , t-1gm , t-1g , t-1m , tgm , tg , tm .
So we have now generated all group elements of the displayed part of the P2mg pattern as given in Figure2. To generate still more elements, we can extend the central column of elements in an upward and downward direction by continuing to apply the glide reflection, and then combining the results with the translations, and thus then working horizontally in both directions.
In the next document we will generate the Plane Group C2mm .
e-mail : 
To continue click HERE for further study of the totally dynamic and holistic nature of Reality.
back to homepage
back to the Ink-in-Glycerine Model
back to Part I of The Crystallization process and the Implicate Order
back to Part II of The Crystallization process and the Implicate Order
back to Part III of The Crystallization process and the Implicate Order
back to Part IV of The Crystallization process and the Implicate Order