Back to Homepage

In Part I (present Part of Website) of the discussion of Aristotelian metaphysics (theory of natures) we said that it was our intention to expound this metaphysics along the lines of Joseph OWENS's interpretation (in his book The doctrine of Being in the Aristotelian Metaphysics, 1951, 1970) of the content of Aristotle's treatises on metaphysics. In order to prepare for it we again investigated the ontological status of Aristotle's Catgories (Substance, Quantity, Quality, Relation, etc.) in the light of OCKHAM's findings in this respect and also in the light of our own findings. After that we expounded and discussed the type of Logic which is in fact founded upon and appropriate to this metaphysics :  Intentional Logic (as it was first proposed by VEATCH, while the latter in turn had based his exposition on findings done by MARITAIN ).
And now it would be time to engage thematically in Aristotle's metaphysics along the lines set out by OWENS.
The key orientation should then accordingly be along the lines of the so-called  pros hen  nature of Being (See for the  pros hen  nature of Being the Section  "The doctrine of the   p r  o s   h e n   equivocals"  in Part I (at the end of the upper third of that document) ).  This nature is a referential structure. It includes instances of (types of) beings but always refers to some primary instance among them. If we follow this referential structure, that is, if we look for a primary instance, starting with the 'accidental' Categories (quantity, quality, relation, etc.), that is starting from mere auxiliary beings, we stepwise ascend to higher and higher, that is, more and more genuine, Being, that is, we find the one primary instance of the types of being which types are collectively represented by the system of Categories. The first genuine type of Being we so obtain is the first of the Categories, namely  Substance (or  Entity,  as OWENS calls it). While the accidental Categories are mere ontologically dependent beings, substance is, within the system of Categories ontologically independent. The accidents ontologically depend on substance, that is, they are 'carried' by substance. So within the system of Categories (as a system of types of Being) the accidents are secondary instances of Being, while substance is the primary instance. And especially in First Part of Website we defined  a  substance  as an individual intrinsic being, which is a being which specifically is what it is  intrinsically, that is to say it intrinsically contains that what it specifically is, and in addition to that it carries certain accidents. Examples are (single) individual crystals and organisms. Such an intrinsic being always is the product (or still an intermediate state) of a certain dynamical system. The dynamical law, governing the succession of states of such a system, then was established (in First Part of Website) to represent the very  essence,  that is the specific intrinsic whatness of the relevant intrinsic thing. In fact this dynamical law was interpreted as the 'genotypical essence' of the thing, while its immediate and necessary material consequences (visible as material structures or behaviors) was interpreted as the 'phenotypical essence' of that same intrinsic being.
But it turns out that this Being or Entity, as it has revealed itself as substance (intrinsic being), has itself a pros hen structure in turn, that is to say, it itself refers to a primary instance again, that is, a one primary instance amids secondary instances. A substance (still in the metaphysical sense) consists of prime matter and substantial form. Substance insofar as it is the  ultimate  substrate (just as substance it is already the substrate of the accidents it carries, but as such is still not the ultimate substrate) of all the content (not just that of the accidents but also that of the substantial form) of the given intrinsic thing is called  prime matter,  and is as such a secondary instance of  substance.  The primary instance is the  substantial form.  However, it seems that even this primary instance of substance has itself  a  pros hen  structure. At least Aristotle seems to point in this direction. The substantial form points to a primary instance again. This new, and certainly ultimate, primary instance of Being is so-called  separate entity.  It is a type of Being which is being in the most pertinent sense, and it is supposed to be immaterial (which the word 'separate' here means). The presence of such 'separate entity' in a way points to an immaterial domain of Being where it resides. The Aristotelian metaphysics does not present further clues as regards to it apart from a reference to the divine nature of this domain.

Earlier  ( Third Part of Website and Fourth Part of Website )  we discussed the very powerful and interesting idea of the  Implicate Order  (as first proposed by BOHM, 1980). Together with so-called Holistic Simplification taking place in the Implicate Order and then in a reversed direction in the Explicate Order ( =  the world as it is in Space and Time) Holistic phenomena as they occur here and there in the space-time world could be explained by invoking the assumed existence of the Implicate Order. But does such an Order actually exist? Initially we surmised that the domain of the 'separate entities', as implied by the doctrine of  pros hen  equivocals in Aristotelian metaphysics, could (thematically) be compared to, or even equated with, BOHM's Implicate Order or some adapted version of it. We would then have an ontological justification of, or even an argument for, the actual existence of such an Implicate Order (alongside with an Explicate Order).
It seems to turn out, however, that aristotelian metaphysics (and also all of its later scholastic extensions) is too narrow to accomplish this. The Implicate Order is supposed to stand in a constant  dynamic  'interaction' with the Explicate Order :  Alongside other things the noëtic (thoughtlike) holistic simplification taking 'place' in the noëtic (and therefore spaceless and timeless) Implicate Order is unfolded (explicated), or, as we can say, is 'projected', into the Explicate Order (that is, it is now unfolded along the space dimensions and along the time dimension of that Order) resulting in a holistic phenomenon taking place in the Explicate Order  ( This was expounded in the Section  "Summary and extension of ontological theory"  in  Fourth Part of Website,  Part XXIX Sequel_4. ).  In aristotelian metaphysics there is, as far as my knowledge goes, nothing that supports such a dynamic interaction by way of projection (and injection) between the material world (sensible world) and the world of 'separate entities'. This is because, although aristotelean metaphysics does take into account  change  (and even purports to explain it ontologically), and so acknowledges  process  and thus  becoming,  its central issue is not process but  being,  that is to say that it interprets  becoming  not as a form or version of  being  (or of  not-being  for that matter) but as a mere intermediate state between  being  and  not-being.
But if we are going to investigate Reality from the viewpoint of constant projection and injection of elementary features taking place between the Explicate and Implicate Order, the (explicate) structures resulting from the composition of such basic features are thoroughly dynamic :  Because of the incessant projection (unfolding [from the Implicate Order into the Explicate Order along the latter's space-time dimensions] and incessant injection (enfolding from the Explicate Order into the spaceless and timeless Implicate Order) of elementary features every explicate structure or pattern (composed of such features) (i.e. all the things we see in our space-time universe) is totally dynamic. It is constantly created anew (See  Third Part of Website ).  And this is not very well compatible with aristotelian metaphysics, that is, there is not enough in this metaphysics to support it. Aristotelian metaphysics is static in the sense that  becoming  is not acknowledged as  being,  let alone as the very  way of being  of things in the space-time world. And according to our present view (which must always be seen as just a preliminary proposal of an alternative view, without degrading or dismissing other views given in this website) the  very way of being  in the space-time world (that is, the sensible world) is  becoming.  Everything in that world is in the process of change, that is in the process of becoming something else. Such processes sometimes are, it is true, very slow, resulting in an apparent constancy or static being, but that is only because of our disability to discern very slow processes without special equipment. So our sensible world is indeed thoroughly dynamic, that is, even already within the Explicate Order. So the being of all the things in the sensible world including the above mentioned 'intrinsic beings' (crystals, organisms, etc.) is just a dynamic state or a few such states out of a long series of different such states successively connected within some given dynamical system. And even such a dynamical system can and will be perturbed, often leading to its disintegration. So even 'intrinsic beings' are not eternal, they are 'slower sections' (slower-going stretches) of an overall ongoing dynamical system or a mixture of such systems.

In aristotelian metaphysics  intrinsic beings,  substances, are central. They are supposed to stand out clearly amids the overall 'static' and 'cacophony' of the sensible world. However, if we assume that this world is thoroughly dynamic, then 'everything causes every thing', nothing stands all by itself, but is constantly bombarded by influences coming from without, that is to say, existing natural dynamical systems are never isolated, they always are connected, loosely or strongly, with in principle all the other existing dynamical systems of the Universe. This means that also any existing intrinsic being is subjected to all kinds of external processes perturbing it from without. But because generally the dynamical system which generates and maintains such a being (for example a crystal developing in a solution or melt) is relatively stable the generated being keeps on to stand out for a relatively long time in its growing environment :  The dynamical system will be perturbed and could then follow a different course, but not for long, because such a system quickly recovers, neutralizes the disturbing factor and takes up its original course again. Some perturbations, however, are too strong, resulting in the original system following a definitive different course and never assuming its original course again, or resulting in the total disintegration of the original dynamical system and with it the disintegration of the being (thing, pattern) that was originally produced. Here it was about intrinsic beings originally produced by a relatively stable dynamical system. Most beings, however, are not intrinsic, they are wholly produced by external factors. These are beings such as sand dunes and in fact all other so-called aggregates. Their form and shape are determined not by a single stable dynamical system, but by a combination of many dynamical systems that happen to be present. Such aggregates therefore do not clearly and persistently stick out from their environment, bur are constantly changing and intermittently totally mixed up with, or engulved by, their environment.
So it is not things (either intrinsic beings or non-intrinsic beings called aggregates) that clearly and persistently stand out. All of them are ephemerous, all of them are in a state of change, and all of them are subjected, weakly or strongly, directly or indirectly, to virtually all other processes taking place in the Universe.
Because of all this it is clear that  becoming  is the typical and dominant  way of being  in the space-time world. And this entails that in the metaphysics dealing with this world the emphasis should be on  determination,  and first of all on  dynamic determination.  That is to say we must develop a metaphysics which, it is true, incorporates the substance-accident metaphysics of Aristotle with its intrinsic beings and aggregates, but at the same time extends itself in such a way as to incorporate and concentrate on  determinative relations  as they occur in the space-time world. In this view we do not then specifically look for one material thing or another and see how it goes its way, but we look for a given global simultaneous overall condition or state  determining  the next global simultaneous condition or state coming after it in Time. In fact we look to the one world process as a whole and try to analyze further its system of successive states, that is, try to analyze its global determinative system into more elementary local determinative units.
Because there is in fact only one global world process and thus only one linear sequence of successive 'world states', we cannot have knowledge of this process, at least not precise knowledge, by reason of the fact that we cannot know any one of the successive 'world states' in sufficient detail. So science (but also everyday life) tries to  isolate  some successive sequences that seem more or less to stand out :  It isolates in such a way as if it has found a certain natural dynamical system that proceeds totally on its own and is not at all influenced by external factors. Of course in reality such systems do not exist, but they sufficiently stand out to allow them to be studied in isolation, for example in experiments that are as much as possible shielded from external factors. In this way science finds the so-called natural laws, such as a law for fluid motion from which weatherforecasts can be made. Because of the shielding off from external influences (and thus abstracting from individual local details) such laws obtain a degree of generality, meaning here that each one of such a law does not tell us anything about the individual deviations that can occur at the very places where the law more or less happens to apply. Thus we all know that to describe or explain the  world process as a whole  by a small number of artificially isolated dynamical systems and their specific laws is only an approximation, sometimes a crude one. But this is the only way natural science can proceed, and when acknowledging the inherent limitation of such an approach it is legitimate, and especially fruitful in the practice of technics.
But  ontology  (which is the theoretical core of metaphysics) has nothing to do with everyday practice or human technical art, so these latter do not determine how it should proceed. It is also not geared to discover details, it only tries to find generalities. So also its unusefulness for finding details does not determine how it should proceed. It must reveal how the world  generally  and  globally  and especially  fundamentally  is in itself, totally independent of being known or not being known, being intended or not being intended by a knower or observer. This ontology now will, because, as has been said, the world consists of determinations and is as such a web of deterministic threads, concentrate on the analysis of this determinative web and reveal the fundamental determinative units or elements by which this web is composed. This determinative web is also called  causal web,  which is correspondingly composed of linear causal sequences, where such a sequence is in fact a successive series of cause-effect units. We'll speak about causality later.

First example of causal interwoveness.
In order to illustrate the interwoveness of all the determinative or causal sequences, we could consider a tennis ball, its initial velocity and direction of motion and the pull of the earth's gravity along its trajectory. As such we can see this as a dynamical system. Its succession of dynamical states corresponds to the succession of (momentary) spatial positions, velocities, and momentary directions of motion along the ball's trajectory. However, a broader view of it reveals that the described dynamical system is just something that is as such artificially isolated ( = insulated), and considered to exist dynamically separated from the rest of the world, especially from all other processes that are going on at the same time. Although in the present example these other processes happen to have little influence on the original dynamical system (the ball, its initial velocity, the pull of gravity) -- which is the reason why this particular system can, at least for practical purposes, be isolated from all other events simultaneously taking place -- the influence nevertheless is there, as the following partial account of a game of tennis shows :  Each time the ball is hit back across the net the very reality of the causal impulse can be felt right down the muscles of the arm. This palpable impact also provides the initial conditions of velocity and position that determine the path of the ball as it speeds toward the net. Gravity also belongs to all this, but does not act as like an initial impact, rather it operates over the whole path of the ball. For all practical purposes, the effects of gravity on the tennis ball are all due to the earth mass. But here the description of the artificially isolated system ends, and from now on we set this system into a broader context :  The minuscule gravitational effects of nearby mountains, the passage of the moon overhead, the sun, the planets of the solar system, the more distant stars and even the masses of the players who run across the court must be taken into account. Another, and now indeed major, influence on the ball's path (and thus on the original dynamical system) is the effect of air resistance, which acts to reduce its velocity. Like gravity, air resistance acts ove the whole path, but unlike gravity, its force strictly depends on how fast the ball is going. The faster the tennis ball travels, the greater are the effects of air resistance, and indeed, when the ball is moving slowly, this force is negligible. Air resistance can be calculated knowing the density of air in the tennis court and the characteristics of the ball and its flight. However, there will also be subtle variations in this resistance, for the air may not be uniform in density. For example its temperature may change over various segments of the court and the effect of an evaporating puddle will be to lower air temperature and increase humidity. All these effects in air resistance add up to very subtle causal correlations that arise from the whole situation of the court, the weather, the temperature, surrounding vegetation, and so on. Finally, there are the effects of currents of air which act to deviate the ball as it travels. When players are dealing with a steady wind they compensate each of their shots. However, it is more difficult to deal with sudden gusts of wind or changes in direction. To trace the origin of the gusts that blow across the tennis court is a particular tall order for the world of causal chains. Their ultimate origin may lie in the earth's daily rotation, which produces what are known as Coriolis forces, which give rise to the great swirls of weather in the northern and southern hemispheres. In addition to these global currents of air there are also the varying effects of the moon's pulling on the earth's atmosphere, temperature changes from region to region, and the complications induced by masses of air flowing across oceans, deserts, and mountain chains. But also on a smaller scale the air and its motions are being worked up in a complicated way :  As air rises up a gentle slope, for example, it is cooled, producing density fluctuations and local gusting. Wind passing across a lake will take up moisture, and as it approaches a city, it will be heated and perturbed by tall buildings. By the time it reaches the tennis court the behavior of any one gust will be the result of such a multitude of complex causes and causal sequences that it lies far beyond the predictive power of even the largest and fastest modern computer.
All other processes we see in our world should be seen in the same way. But then we must admit that the dynamical world is utterly complex, far to complex to be understood.
So it is quite understandable that science does not attempt to understand the whole system of such causal connections and cross connections, that is to say, it does not have the ambition to understand or going to understand the world process as a whole in all its details of interconnection, but perforce conceptually isolates (insulates) certain sequences of observed states from most 'perturbing' actions coming from their surroundings, and so drastically reduces the number of factors to be investigated, factors having their (often small) effect on such a sequence of states. But it is also clear that such a conceptual isolation renders the successive sequence of events (the dynamical system)  general,  that is to say the sequence (dynamical system) has as such obtained a degree of generality, because in virtue of the (conceptual) isolation individual circumstances are left out of consideration, rendering the sequence non-individual, and thus general. Said differently, leaving out of consideration the completeness of the set of simultaneous individual conditions (that is, considering at most an incomplete set of such conditions), the sequence of events on which one concentrates is not completely determined, and therefore has a degree of generality, that is, a degree of indeterminateness. For the practice of natural science, and also of everyday life, such an approach (conceptual isolation of sequences) is perfectly legitimate. Not, however, for ontology. There we are interested in the fundamental structure, and presently especially the fundamental determinative structure of the world. And when determinations (as causal chains) happen to show intricate ramifications or branchings, then it be so, and must be investigated as such, that is, not with the help of idealizations (for example the assumption that a local dynamical system or successive sequence of events is not in any way affected by other systems or events taking place simultaneously) but as they really are. Of course we then cannot arrive at a knowledge that allows us to make (approximate) predictions, but, as has been said, this is not the goal of ontology.

Second example of causal interwoveness.
In order to show the interwoveness of determinative chains everywhere in the space-time world, another example may be instructive. It is about a falling physical object. Very accurate experiments, to determine the acceleration due to gravity using a falling body, have from time to time been carried out. But to eliminate all contingencies and extraneous causes requires the resources of a major standards laboratory. A number of decades ago an experiment, using a falling metal bar, was designed at the National Research Council of Canada. David PEAT, as he reports it in his book  Synchronicity, 1987, pp.49, had the opportunity to talk to the various scientists and technicians about their experiments.
In order to insulate the experiment and the particular effect -- the acceleration due to gravity -- from the rest of the universe, many hundreds of person-hours were spent in designing and constructing apparatus which extended into several rooms. To begin with, the tube down which the bar would fall had to be evacuated to remove the effects of air resistance. In addition, the drop had to be carefully shielded to eleminate all electrical and magnetic forces on the bar. The whole apparatus had to be precisely temperature controlled to eliminate changes in length of the bar due to expansion and contraction. Timing was done using an atomic clock, and any earth tremors, which would perturb the local gravitational force and, moreover, act to vibrate the apparatus, were monitored. Even the way in which the bar was released had to be carefully designed, for if one edge were to be released a fraction of a second before the other, this would start the bar vibrating and oscillating.
With all the resources of a major research institute, an attempt was made to eliminate the effects of the universe from this experiment and to create ideal, insulated, and repeatable conditions in which to measure the acceleration due to gravity. But even with all this effort, each experiment differed slightly in its result. The final value was therefore obtained by averaging, but even after all the experimental errors and deviations had been taken into account, the averages over two separate series of measurements were still different by a significant degree. So even during something as straightforward as the fall of a metal bar, nature conspires to introduce fluctuations into each individual event.

So here we see again that in reality events are never happening alone, but are interwoven in the determinative web or fabric of the whole world. When the particular dynamical system -- insofar as we can legitimately speak of such a sequence of events as  a  particular dynamical system -- is relatively stable, we can, for scientific or practical purposes, conceptually insulate it and treat it as if it were not perturbed by any extraneous factors or other dynamical systems operating at the same time. In such cases we can more or less accurately predict future states of the system. But when the system is a so-called 'chaotic' but nevertheless deterministic dynamical system, already the very smallest perturbation of the system is sufficient to confuse the initial order and to make impossible any more or less long-term predictions. This means that such systems are extremely sensitive to changes in initial conditions (or any state or condition somewhere along the system's dynamical trajectory), that is, very small perturbations can deflect the system's original course dramatically.
All this means that, at least ontologically seen, everything is determinatively (one could say causally) connected with everything else in the universe. Although many such connections are weak and indirect (and therefore insignificant for everyday life and even for natural science), they are there nevertheless, and ontology must take that into account. All the foregoing indicates that in fact no isolated processes exist in the space-time world, implying that there is in fact only one process, that is, one single overall 'world process', a process whose dynamical states together form a successive series of world collocations. Every such particular collocation or particular state of the 'world system' is  a  pattern of simultaneous co-existence of beings  of whatever sort. A main characteristic and determining factor of such a collocation (that is, what it must, or can, be, and what it cannot be) is the fact that the beings in it are such that they indeed can co-exist together, at least at that particular point in time. They may vanish in the next state of the world system. And, as we have already said, despite the fact that there is in reality only one dynamical system -- the 'world system' -- some 'subsystems' can be conceptually insulated for the purposes of science and everyday life, because at many places the determinative cross connections (connecting systems causally with other systems) turn out to be very weak. The world process consists, as has been said, of a successive series of world collocations, each of them being  a  simultaneity section  through the whole universe. Each such a section is produced by the previous section, because such sections are the successive states or stages of the one world process. And in every next moment (in Time) a new state is formed. And each such a 'world state' is a spatial pattern of all beings co-existing simultaneously at the moment when the state was created. So the world process shows two types of determination, viz., a simultaneous determination (which is about the compatibility of many different simultaneous beings with each other in order to be able to co-exist), and a successive determination, that is the determination of one world state by the previous one (where then the previous one disappears). The simultaneous part involves three-dimensional space, i.e. it is along the space dimensions, while the successive part involves the time dimension, that is, it is along that dimension. This latter dimension is perpendicular to all three space dimensions.
The next figure diagrammatically depicts the determinative structure the 'world system' (that is the one all-encompassing world dynamical system).

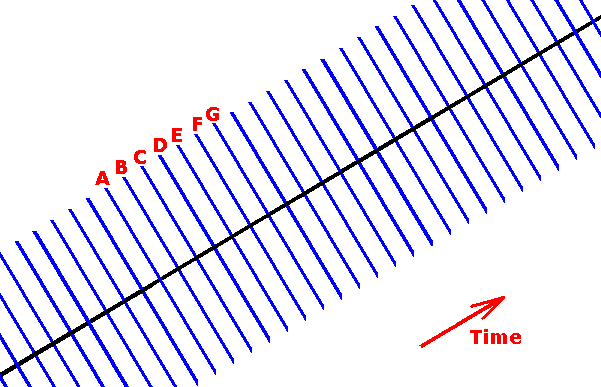
Figure 1 :  Diagrammatic picture of the world process. The world process is a succession of spatial simultaneity sections (blue lines) through the whole world. Each such a section is generated by the previous one. The time dimension and direction is indicated. The three space dimensions are perpendicular to the one time dimension. They are symbolized by each blue transverse line. A number of successive world states are symbolized by the letters A, B, C, D, E, F, and G. Every such symbol refers to the whole transverse line present at both sides of the line expressing the successivity.

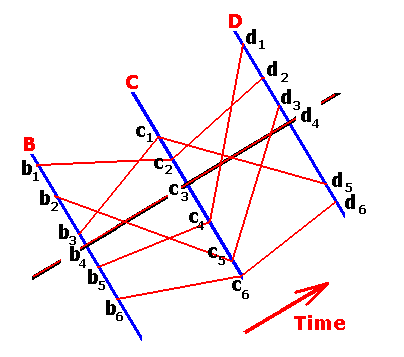
Figure 2 :  Blow-up of a part -- world states B-C-D -- of  Figure 1,  revealing the determinative fine-structure.
World state  B  is the complete cause of world state  C,  and world state  C  is the complete cause of world state  D.
Every complete cause consists of a number of  partial causes,  and to each such a partial cause of a given complete cause corresponds a partial effect in the next world state (which itself is the complete effect).
Accordingly, the complete cause  B  consists of a number of partial causes, of which six are depicted (as examples) :  b₁, b₂, b₃, b₄, b₅, and b₆.
These partial causes produce their corresponding partial effects in world state  C  :  c₂, c₅, c₁, c₃, c₄, and c₆.  These latter in turn are partial causes constituting the complete cause  C.  And these partial causes produce their corresponding partial effects in world state  D  :  d₂, d₃, d₅, d₄, d₁, and d₆.
Roughly the same type of fine-structure will be found between all other world states.

In Figure 2 we see that the determination between any two world states is made up of many more elementary determinative elements, where such an element is seen to be the connection of a partial cause with its corresponding effect. For the world states  B-C-D  12 such elementary determinative connections or links were depicted :

From world state  B  to world state  C  :

b₁ ---- c₂
b₂ ---- c₅
b₃ ---- c₁
b₄ ---- c₃
b₅ ---- c₄
b₆ ---- c₆

From world state  C  to world state  D  :

c₂ ---- d₂
c₅ ---- d₃
c₁ ---- d₅
c₃ ---- d₄
c₄ ---- d₁
c₆ ---- d₆

It could be that the discussed and listed partial causes and their corresponding partial effects themselves have a fine-structure in turn, resulting in still more elementary determinative connections. If we, however, for simplicity's sake, assume that the just discussed determinative connections are already the  most elementary  determinative connections, then we have to do with the very basic or 'last' determinative elements (in the sense of the ultimate elementary, and therefore smallest, determinative steps, here as such distinguished only insofar as they are (so) elementary) which (elements), together with many more such in-the-same-degree basic determinative elements, constitute the total and complete determinative structure of the space-time world.
What precisely are these elementary determinative elements? Have we met them before? In a way we have :
In Part I of Fourth Part of Website )  we have discussed the theory of  If-Then constants  (the reader should consult this Part). There they were interpreted as principles of determinative connections :  Such a principle then determines that  if  the sufficient ground for some specified feature or pattern X does exist in the space-time world,  then  X necessarily exists. We have listed many such  If-Then constants. Together they were supposed to constitute the determinative structure (Nomos) of the world (Cosmos).
In the present exposition, however, we will take these constants in a slightly different way.
First of all we take as the very  "genuine and true  If-Then constants"  only those that represent, or are at least meant to represent, the above discussed  elementary  determinative connections. All other sometimes so called  If-Then constants  are here considered not as genuine If-Then constants, but as determinative connections that are not yet elementary, but composed of still more basic determinative connections. Only when we arrive at determinative connections that are absolutely elementary, and thus are not composed anymore of still more basic determinative connections, we have arrived at genuine  If-Then constants.
In practice it is in most cases not possible to unearth such genuine constants, so we will once and for all agree that when we, in the present discussion and in all that comes after it, speak about, and give examples of, If-Then constants, we MEAN the  genuine  If-Then constants representing the absolutely elementary determinative elements (connections, links) whatever the examples used.
Further, we will ascribe a certain degree of generality to our If-Then constants, that is, they are principles that do not determine any being or event completely all the way down to individuality, but only precisely (and as such completely) determine that for which their Then term (that is, their consequent) stands, and this term does not stand for something individual. True individuality and one-offness is only the result of many different such constants applying together for a given case. And things, features or events can only exist (in the space-time world) when they are individuated.
Any If-Then constant consists of three parts, viz., an  If term (that is, an antecedent), an implication (==>), and a Then term (that is, a consequent). If that for which the antecedent stands exists, then that for which the consequent stands must also exist. As has been said, every If-Then constant has a certain degree of generality, which first of all means that it is in fact the Then term which has that degree of generality, which in turn means that the Then term can only be realized (as existing in the space-time world) when other If-Then terms also apply and together result in individual existence. And it is because of this degree of generality of the Then term that the  If term can and must be  disjunctive.  Indeed, a not yet completely determined feature or thing, let us call it A, can have several or even many possible different sufficient grounds, say the grounds  a, b, c, d, e, f, g, h,  implying (that is, guaranteeing) its existence. The corresponding If-Then constant then reads :

If  a  or  b  or  c  or  d  or  e  or  f  or  g  or  h  exists,  then   A  must exist.

So the condition   a  existing alone is already sufficient for  A  to exist. And in the same way   b  existing alone is also already sufficient for  A  to exist. The same goes for the other conditions, c, d, e, f, g, and  h.

Well, each determinative connection, considered to be absolutely basic, depicted in  Figure 2 ,  is a special case of an (ontological, that is, natural and automatical) 'application' of a particular  If-Then constant. Let us give this Figure again, and work things out further.

Figure 2 :  Blow-up of a part -- world states B-C-D -- of  Figure 1,  revealing the determinative fine-structure. Each red line, leading from one world state to the next, stands for the application of a certain  If-Then constant  to the existence of one condition out of the constant's set of possible conditions (See below).

The basic determinative connection (basic elementary determinative link)  b₁ ---- c₂  (to take just an example) is here a special case of an application of the following  If-Then constant,  which could read :

If  a  or  b₁  or  c  or  d  or  e  or  f  exists,  then   c ₂  must exist.

In the context of Figure 2 the condition  b₁  is supposed to exist. And this means that the just given If-Then constant applies (this is the mentioned  special case of an application ).  It would also have applied when one of the other conditions, a, c, d, e, or  f  existed.
For the other basic determinative connections given in Figure 2 we can say precisely the same. Also each one of them is a special application of a certain If-Then constant. And as such it represents such an If-Then constant. But if this  If-Then constant  is  fully  expressed, then, of course, the disjunctivity of the  If term must be expressed, that is, all the possible conditions or sufficient grounds must be included.
If we do not want to do this explicitly (for example because alternative sufficient grounds are not [completely] known), then we could, in the case of the If-Then constant

If  a  or  b₁  or  c  or  d  or  e  or  f  exists,  then   c ₂  must exist,

simply refer to this constant as the

" If-Then constant for  c ₂ ".

In the context of Figure 2 one of the possible sufficient grounds, namely  b₁ ,  exists, which then -- according to the If-Then constant -- guarantees the existence of  c₂ .

All the other basic determinative connections of Figure 2 (red lines) we can treat in the same way. Each one of them is an application of the If-Then constant to a particular existing individual case (that is, the actual existence of one out of the constant's set of possible sufficient grounds or conditions). So we can say :

From world state  B  to world state  C  we have the following determinative connections (links) :

b₁ ====> c₂ ,  which is an application of the If-Then constant for  c₂  to the particular case of the existence of the condition  b₁ .
b₂ ====> c₅ ,  which is an application of the If-Then constant for  c₅  to the particular case of the existence of the condition  b₂ .
b₃ ====> c₁ ,  which is an application of the If-Then constant for  c₁  to the particular case of the existence of the condition  b₃ .
b₄ ====> c₃ ,  which is an application of the If-Then constant for  c₃  to the particular case of the existence of the condition  b₄ .
b₅ ====> c₄ ,  which is an application of the If-Then constant for  c₄  to the particular case of the existence of the condition  b₅ .
b₆ ====> c₆ ,  which is an application of the If-Then constant for  c₆  to the particular case of the existence of the condition  b₆ .

From world state  C  to world state  D  we have the following determinative connections (links) :

c₂ ====> d₂ ,  which is an application of the If-Then constant for  d₂  to the particular case of the existence of the condition  c₂ .
c₅ ====> d₃ ,  which is an application of the If-Then constant for  d₃  to the particular case of the existence of the condition  c₅ .
c₁ ====> d₅ ,  which is an application of the If-Then constant for  d₅  to the particular case of the existence of the condition  c₁ .
c₃ ====> d₄ ,  which is an application of the If-Then constant for  d₄  to the particular case of the existence of the condition  c₃ .
c₄ ====> d₁ ,  which is an application of the If-Then constant for  d₁  to the particular case of the existence of the condition  c₄ .
c₆ ====> d₆ ,  which is an application of the If-Then constant for  d₆  to the particular case of the existence of the condition  c₆ .

This kind of situation obtains between every two successive world states.

Generally, the If-Then constant for X has as its antecedent (that is, the If term) the disjunctive list of all possible sufficient grounds or conditions for the existence of X. Such conditions can be all sorts of features, things or patterns, each one of them alone already guaranteeing the existence of X.  A condition or sufficient ground for X, insofar as that ground figures  dynamically ,  is a cause of X (and a partial cause of the corresponding world state in which X resides). This cause of X resides not somewhere in the world state in which X resides, but somewhere in the previous world state. And, having said this, the world process  ( = world dynamical system, consisting of a succession of world states) could be such that a small part of some given world state is repeated in a (limited) number of world states that come next. And it could be that our X is such a small part (or part of the latter) that is repeated in the next world state, repeated again in the next next world state, and so on for a number of times.
An explanation for this could be that, to begin with, at some time X is generated from W. The (complete) world state WS_n is the complete cause of the next (complete) world state WS_n+1 .  If we assume that W resides in world state WS_n ,  then W is a partial cause of world state WS_n+1 ,  that is, of the next world state, which itself is the complete effect of the previous world state. And then X is a partial effect of that previous world state. Now it could be that the world state which comes after WS_n+1  (which contains X),  that is, the world state WS_n+2 ,  also contains X at the corresponding location of this word state. So X is repeated in the next world state. This could go on indefinitely, or only a finite number of times, the last repetition then taking place, say, in world state WS_n+583 .  The next world state -- WS_n+584 -- does not have X anymore, but, say, Y. Thus we have, embedded within the succession of (complete) world states, the sequence  W ==> X ==> X ==> X ==> X ==> ... ==> X ==> X ==> Y ==>.  And this means that we have for a number of times  X ==> X.  And where we have  W ==> X ,  W must be the cause of X, and this cause must consist of two 'elements' or aspects, viz., a generating cause and a sustaining cause. This is so because in order for X to exist (at a certain location) it must not only once be generated at that location (or generated else and then moved to this location), but it must at the same time be sustained in order to remain (that is, tend to remain), existent. At least it must have the tendency to remain existent.
For example, if an ice crystal is to exist at some location it must have been generated (there), and for this (generation) freen water molecules must have been present in sufficient numbers. In addition, the ambient temperature must have been below zero during crystalization. But for the ice crystal not just to exist only for a split second, but having at least the tendency to remain existent, the ambient temperature must remain below zero, and (other) conditions must be such that the crystal will not directly evaporate again. These are what we would like to call  sustaining causes :  the crystal may, it is true, not grow larger anymore, but it keeps on existing, or at least tends to do so.
When we now consider the sequence  X ==> X ==> X ==> X ...,  we can say that that sequence does not need the presence or existence of the  generating  cause for X, but it does need, and thus implies, the  sustaining  cause of X to be present at the corresponding location in all the (complete) world states that correspond to the members of the sequence  X ==> X ==> X ==> X ... .  As long as this sustaining cause is not annihilated (by the system being perturbed from outside), X will be repeated. That is, everytime it will reappear in the corresponding location of the next world state.
Now we must interpret this in terms of the If-Then constant for X.
As we have said, the antecedent (that is, the If term) of the If-Then constant for X, is a disjunctive list of all possible sufficient grounds or conditions for the existence of X. Now we know that one of these possible sufficient grounds or conditions is :  the presence of X itself plus one or another of its possible sustaining causes.
So with the event  X ==> X  we have not discovered a new type of If-Then constant (where the If term equaled the Then term), but only a new (type of) member of the disjunctive list of possible sufficient grounds or conditions for the existence of that for which the constant's Then term stands. The actual event  X ==> X  is just an application of the one If-Then constant which could read :

If  A  or  D  or  W  or  D  or  E  or  X  (and its sustaining cause) exists,  then   X  must exist,

and indeed we get X, because X exists. That is, X will appear at the corresponding location of the next world state, because it (and its sustaining cause) was present in the previous world state.

Earlier we spoke about the dependence of all dynamical systems (discernable in the space-time world) upon each other, that is their causally being connected with each other. How do  If-Then constants  -- as defined above -- fit in this picture? And how must we understand this dependence?
As we have already said, there is in fact but one dynamical system, the world process. Nevertheless some subsystems can conceptually more or less be insulated from their environment. That is to say, within the overall world process as the one dynamical system, some subsystems can be discerned. These latter are not independent from each other or from their environment, but their dependence is relatively weak, meaning their sensitivity to perturbation of one or more of their states, is relatively low, allowing them to be conceptually insulated for the sake of natural science or even of everyday life. Some such subsystems are relatively stable, meaning that most perturbations do not have an enduring effect on the perturbed system because the latter quickly restores its original course. But other subsystems are more or less unstable, by reason of which they will either definitively follow a new course after having been even only lightly perturbed, or even totally disintegrate.
The causal connection between two different subsystems consists in the application of one or more  If-Then constants  that have their  If component in a state of one dynamical subsystem and their  Then component in a state of the other dynamical subsystem.
The following diagrams try to depict all this.

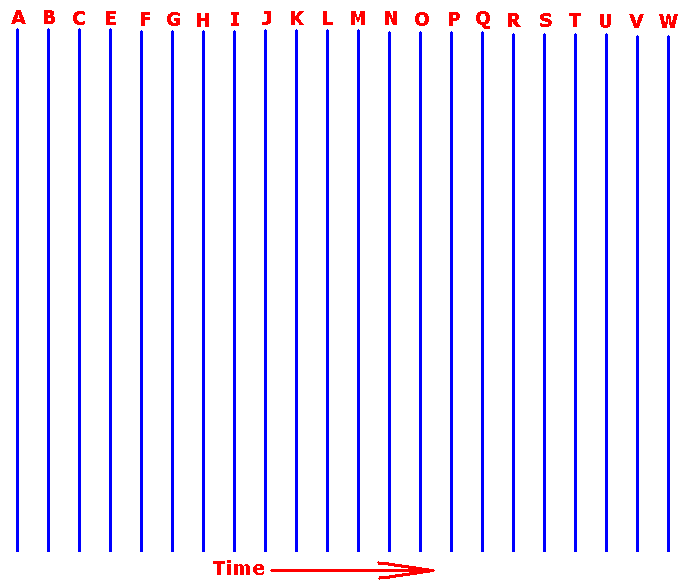
Figure 3 :  World states (blue lines) A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W (and more) as successive states (stadia, stages) of the world dynamical system. Each such a state (stadium, stage) is  a  simultaneity section  through the whole universe. The determinative fine-structure (applications of  If-Then constants) not yet drawn.

Before we analyze this one dynamical system (world system) into a number of different dynamical subsystems that can more or less be insulated, we first depict what it exactly means that two subsystems are interacting with each other.

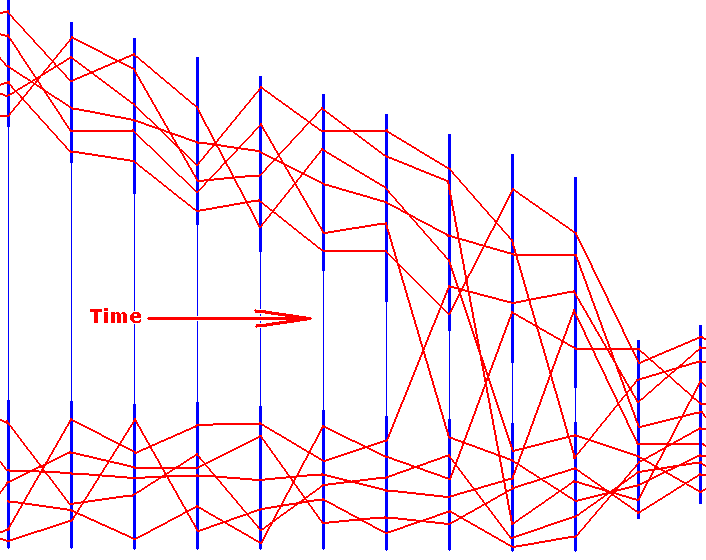
Figure 3a :  Two dynamical subsystems following their course and finally strongly interacting with each other resulting in them to merge together.
The vertical blue lines represent the successive world states, that is, the states of the one overall world dynamical system. These world states are the simultaneity sections through the whole universe. The thin sections of the (blue) lines representing the world states indicate -- where they are drawn -- the initial low degree of dependence of the one subsystem from the other as a result of a low degree of interaction. Also the 'distance', as drawn between the two subsystems, symbolizes the degree of interaction between them (large distance, low degree of interaction).
Any continuous  thick  part of a given blue line represents the state of one  subsystem. The other continuous thick part of the same line represents the state of the other  subsystem. Both states belong to the same world state and are therefore simultaneous.
Any red line drawn between two successive world states (successive -- from left to right -- blue lines) is here considered to represent the application of a particular If-Then constant.
At the right side of the diagram the two subsystems are beginning to perturb each other, that is, interact with each other. This happens by virtue of some If-Then constants (in fact their particular applications) spanning the two subsystems. That is to say, the antecedent of such an If-Then constant lies in a state of one of the subsystems, while the consequent of that same If-Then constant lies in a state of the other subsystem, which state is a partial state of the next (in time) world state.

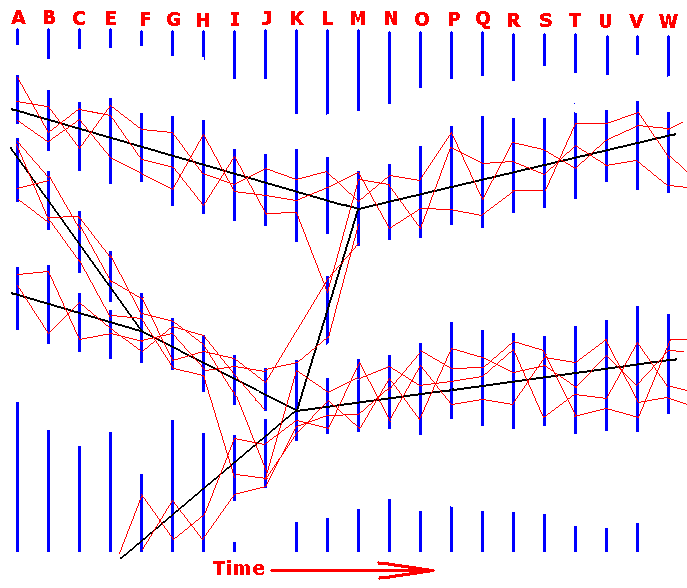
Figure 4 :  A number of subsystems (emphasized by black lines) is discernible within the one overall world system (itself consisting of the successive world states A --- W ).  Such subsystems actually are never completely isolated from each other but interact more or less strongly with each other at several places. After such interactions or perturbations original courses of involved subsystems can be deflected either temporarily or definitively.
Every red line drawn between two consecutive world states (i.e. between one given state and the immediately next one) stands for the application of one or another If-Then constant  to  some particular existing member of the set of possible sufficient grounds for that for which the constant's Then term stands. Here only those applications are depicted (red lines) that are involved in the courses of the considered subsystems and their interactions.

From what has been said so far, it is now clear that every subsystem is in fact a succession of states, which are in fact partial states of the corresponding complete states of the one world process, but which partial states are nevertheless such that they can conceptually be insulated from the rest, and with them the subsystem itself, which now is one of the many more or less particular dynamical systems or natural processes distinguished by natural science. The latter describes these dynamical systems as obeying so-called natural laws. Generally such a law dictates the quantitative relation between any two successive states (one state and the next state). And then, given some one state, the states that went before and those which will come after it, can be predicted. Application of such a law is not restricted to one particular case. It can be applied wherever and whenever it is relevant. This is not epistemologically meant (that is, it is not meant in the sense that scientists can apply such a law wherever and whenever it seems relevant to them), but ontologically. For instance the law of gravitational attraction applies anywhere as long as there are material bodies present. And it is precisely because of the inherent possibility of  repeated  application that we speak about  lawfulness  in the sense of regularity. In fact the many different  natural laws,  as they have been found by natural science, express, as laws, the classification (typification) of dynamical courses (trajectories) of subsystems. And we know that a course of a given dynamical system (as subsystem of the world system) is the succession of its states, and that allways the next state is determined by the previous state. And we know further that this determination consists of the application of a number of If-Then constants, which span between any two consecutive states :

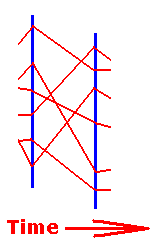
Figure 5 :  Two consecutive states (blue vertical lines) of a subsystem. The next state (i.e. the one on the right) is completely determined by the application (in an ontological sense) of several If-Then constants (red lines) having their antecedent in one state (i.e. the one on the left) and their consequent in the next state.

Before we discuss -- in an introductory way -- modality, we should state the following :
In contrast to what we did in  Fourth Part of Website ,  we here (that is, in the present investigation) do not consider the real world (in the sense of just the world around us including ourselves) to consist of ontologically different layers. If we can discern layers at all, these are only complexity layers. Indeed, organisms are more complex than inorganic things, and conscious living beings are more complex than mere animals. But now these differences are not considered anymore to be brought about by the appearance of something  ontologically  new, but only by a difference in the degree of material complexity. So according to this view the whole real world (including inorganic things, organisms, human beings) is ontologically homogeneous. And this homogeneous real world is meant when we spoke above (and will speak below) about the  space-time world  (which is only to be contrasted with something like the mathematical world). We can also call it the  material world.
This is not meant to refute the  theory of ontological Layers  as it was laid down in Fourth Part of Website (and inspired by HARTMANN, 1940), but only to present an alternative view. Things like this we have done earlier, and the intention simply is to provide the reader with a number of possible different views which he or she then can compare with each other (and with his or her own views). Only in this way, and not by defending during one's whole life only a single view, one can -- I think -- go forward in philosophy. Indeed, philosophy should remain a dialogue, not an ideology.

Now let us say something preliminary with respect to the modality or modal structure of the space-time world.
Generally, the  modality  of some given defined world is saying something about the determinative status of its existents, which means whether a given existing being, feature or event in this world exists  by necessity  or exists  by pure chance  (that is,  by coincidence ),  and what it means that a certain being, feature or event, is  possible  (or  impossible  for that matter), and finally what it means that a certain being, feature or event, is  real  (or  not real  for that matter). This determinative status is here meant in an  ontological  sense, not in a mathematical sense, not in a logical sense, not in the everyday sense, and also not in an epistemological sense. When we speak about the  m o d a l i t y  here  (that is, in the present investigation), we have in mind the modality of the  space-time world  as it, and its modality, actually   is  (or turns out to be)  all by itself  and totally independent of any knowledge of the things in this world.
First of all, modality refers to  here-and-now-existing  things, features or patterns. Such a thing, feature or pattern need not to be something having a certain degree of generality (here and now existing), but can be any thing, feature or pattern (whether general, specific, or one-off) here and now existing in the space-time world. Of such an existing thing, feature or pattern we then ask (1) whether it must then be also possible or (2) whether it exists by pure chance (that is, without having a cause ground or condition), or (3) whether it exists necessarily.  Discussing the modality of the space-time world in a strict philosophical and ontological way is not :  having in mind a certain thing, feature or pattern (without pointing to it as existing), and then ask (1) whether in the space-time world such an imagined thing, feature or pattern is possible,  or (2) whether it can come to exist in the space-time world just by pure chance without being caused or conditioned,  or (3) whether, if it is, for the sake of theory, (just) taken to exist somewhere in the space-time world, it exists there necessarily. This way of considering modality belongs to everyday life and human planning activities. There it is perfectly legitimate and natural. But philosophically and especially ontologically discussing and investigating the modality of the space-time world means that our point of departure and point of reference is always a thing, feature or pattern here and now existing in the space-time world, where "here" can be at any one specified location in the universe, and "now" can be any one specified point in time whether in the present, in a particular past or in a particular future. When in the present, the whole discussion sets itself in this present. When in the past, the whole discussion sets itself in this past. When in the future, the whole discussion sets itself in this future.

The following situation is perfectly compatible with the space-time world :  Some specified thing (feature or pattern) exists somewhere in the space-time world while it is not present at some other specified location at the same time.
This legitimate situation makes it possible to consider "not-existing"  as just another modality state in addition to the other ones, viz.,  existing,  possibility,  necessity,  and  fortuitousness.  And indeed, now having  not-existing  as a modality state we also have  "impossibility"  as yet another modality state. So the modalities that could presumably be encountered in the space-time world are :

1.   Necessity
2.   Existing ( = to be real )
3.   Possibility
4.   Fortuitousness
5.   Not-existing ( = to be unreal )
6.   Impossibility

We must now investigate whether indeed all six listed modality states can in principle apply in the space-time world, and what their relationships (for example mutual or one-sided dependencies, or implications) are in such a world.
First of all,  existing  is a modality state fully compatible with the structure of the space-time world, because there indeed are existing things in the space-time world, and all other modality states ultimately refer to existing things.
Now it is clear that at least in the space-time world, if a thing A exists, (here and now), then it must at the same time be possible. Otherwise it would be impossible and therefore not existing. This  being possible  of A could refer to A's mere compatibility with all things present in the simultaneity section in which A resides. Indeed A's existence then would depend solely on the presence of the sustaining cause of A, or at least on the absence of any thing or feature that would prevent A's existence (at that location and time). As such the existence of A could be gratuitous (fortuitous), that is, completely by chance. It just happens to be there and it just happens to be entirely compatible with all other things simultaneously present, and therefore it happily co-exists with them. Here we then have the modality state  fortuitousness.  But in the space-time world any thing or feature does not only have a sustaining cause, but also a generating cause. At that particular time and at that particular location it must be generated in the first place. We assert this on the basis of our conviction that the space-time world -- all of it -- is totally dynamic and that the major way of being of its members is not just  to be there,  but  becoming.  So when we say that A exists, we know that A must not only be able to co-exist with its whole environment, but also that A has become  in some way,  that is, that it has emerged from something else, and that it may still be in the process of becoming. From this it follows that A's existence (or the existence of any other thing for that matter) does not only depend -- and thus A be possible or impossible -- on the presence of some sustaining cause, but also on some generating cause. This generating cause must have been there, immediately preceding the emergence of A. If we consider the existence of A to be a state of some dynamical system or a part of such a state, then the generating cause of A must  be, or at least reside in, the previous state. And for A to be  possible  at all, this generating cause must have been present (and as such immediately preceding the emergence of A) together with a concurring sustaining cause. This means that at least in the space-time world the thing  A  (and with it all other things and features) cannot just pop up without anything having it generated, which in turn means that in the space-time world a thing cannot be there by pure chance. So the modality state  fortuitousness  ( = complete coincidence) has no place in the space-time world.
So we have found out that when a thing or feature exists it must at the same time be possible, and in the space-time world this means that the mentioned causal conditions (sustaining and generating cause) must have been fulfilled. But then it immediately follows that the (here and now) existence of that thing must at the same time be  a  necessary  existence. So we can say that everything that exists at a certain point in time in the space-time world not only is also possible but even necessary at that same point in time.

In the space-time world all existing things are necessarily existing. If the causal conditions are not completely fulfilled at a certain location and point in time, then the thing does not exist at that location and point in time because it is impossible (at that location and point in time).

And now we see that all this is perfectly compatible with the above idea that ultimately the space-time world is determined by If-Then constants. Indeed, it is the ruling of the If-Then constants at the most basic level that brings in an all-out necessity at all levels. Said differently, the particular modality structure of the space-time world, as this structure has turned out to be, is fully in harmony with the determinative structure based on the all-out ontological application of If-Then constants.

In the space-time world an existing thing that is possible and necessary -- let us abbreviate this as a  "necessary thing" -- must have a condition being fulfilled (a condition composed of generating and sustaining cause). Likewise an If-Then constant consists of a condition and that to which the condition applies.
However, an If-Then constant is a principle referring to possible existents, that is, it is not those existents themselves, but refers to them (by its terms), while a necessary thing is an actually existing concrete entity. Moreover, and in a way following from it, while the  necessary thing  is a here and now existing concrete individual thing or feature with its content totally present, meaning that it has not any degree of generality,  the Then term of the If-Then constant refers to something that might exist at some or other location and at some or other point in time, but does not necessarily actually exist at all. Further, that to which the Then term refers has a certain degree of generality. And while the condition of the (existence of the) necessary thing is a one-off condition, a condition, that is to say, that is individual and completely determined, because the necessary thing itself is one-off, individual and completely determined,  the condition as referred to by the If term of the If-Then constant is, as we know, a disjunctive set of all possible conditions or sufficient grounds.
Finally, the  necessary thing  can be every concrete thing, feature or pattern whatsoever. It is not necessarily something fundamental or elementary. Likewise its condition (making it possible, and therefore existent) does not need to be something fundamental or elementary. In contrast, the If term of the If-Then constant, and also its Then term, exclusively refer to something elementary, because the If-Then constant, in the form of its application, that is, in the form of having two things determinatively connected, is considered to be itself the basic unit or element of determination.

Above we said about an If-Then constant that it is a principle referring to possible existents, that is, it is not those existents themselves, but refers to them (by its terms). When, in the space-time world at a given location and at a given point in time, nothing that is signified by the If term and by the Then term of some given If-Then constant actually exists, the If-Then constant is still valid. This is because it does not 'assert' the existence of anything (in the space-time world). So in a way the If-Then constant is still 'present' at the mentioned location and point in time, even when nothing to which its terms refer actually exists there.
From this it follows that an If-Then constant, that is, any If-Then constant, is not a thing, in the sense of not a material thing or material pattern, but some immaterial form. It is not an immaterial form in the sense of  abstracted from matter,  because, as has just been explained, it can be present there where there is nothing to which its terms refer, and nothing that is, or could be, a specific ontological substrate that carries it and, in a sense, make it material. But then there is litterally no place for an If-Then constant in the space-time world.
So If-Then constants must reside in some other sphere of Being the inhabitants of which are all immaterial. But now we must realize that they are not mere immaterial contents existing just for and in themselves. On the contrary, they are  principles  determining states of affairs in the space-time world. And this means that the mentioned "other sphere of Being" in which the If-Then constants reside cannot exist totally separated from the material world (the space-time world), it cannot be totally disconnected with the latter. The If-Then constants must  apply  in the material world (namely there and then where one or other condition, [occurring] in the disjunctive set of all possible conditions referred to by a constant's If term, happens to be met). So the two domains (one harboring the If-Then constants, the other being the proper range of application of them) must in some way contain each other.
And indeed, in  Third Part of Website  we have already discussed such domains of Being that contain each other, namely the Explicate and Implicate Orders. In discussing these orders here we will not follow everything we said there (including what we said about them in  Fourth Part of Website ,  Part XXIX Sequel-1 somewhat past the middle of the document). We will consider the space-time world as being ontologically homogeneous, which now implies that the Explicate Order, which is taken to coincide with the space-time world, is not ontologically layered. The Implicate Order's inhabitants are immaterial. They are supposed to be more or less thought-like, which we had indicated earlier by the term  "noëtic",  namely by saying that the Implicate Order is a noëtic domain of Being. The Explicate and Implicate Orders are dynamically connected with each other. There is an incessant 'projection' and 'injection' taking place :  projection of features from the Implicate Order into the Explicate Order, and injection of features from the Explicate Order back again into the Implicate Order.
Projection of (a copy of) some content or form from the Implicate Order (enfolded Order) into the Explicate Order is in fact an unfolding or 'spreading out' of that (originally noëtic) content along the space and time dimensions of the Explicate Order (the unfolded Order), which in fact means that that content is set within a space-time framework and thus that it  appears  (there and then) in the space-time world.
Injection  of (a copy of) some content or form from the Explicate Order into the Implicate Order is in fact the enfoldment of it. That is to say the content, originally being 'spead out' along the space and time dimensions of the Explicate Order, is having this 'being spread out' undone, resulting in it to be enfolded and becoming noëtic, and thus becoming an inhabitant of the Implicate Order. As has been said, this projection and injection of contents or forms is constantly and everywhere taking place and as such constituting the dynamic connection between the two Orders. Now it is clear that structures residing in one Order can determine structures in the other Order. In a way this is what is going on :  Features or patterns can appear in the Explicate Order, by being projected from the Implicate Order. But they can be injected back into the Implicate Order and so altering this Order in a way. But although it is conceivable that such determination is mutual as described, we assume that the categorical determination, that is, the category-concretum determination (or, equivalently, the determination by a principle of that to which the principle applies) is a one-way determination. We assume that such principles or categories exclusively reside in the Implicate Order (because they are immaterial), and among these principles are surely all the If-Then constants. As we know, any If-Then constant is such that its If term refers to a (complete) set of possible sufficient conditions (that is, conditions for the actual existence of that to which its Then term refers). So that to which the If term of any If-Then constant refers can never be some individual concrete thing feature or pattern, and thus can never be an entity of the space-time world, and therefore not (an entity) of the Explicate Order. This state of affairs is already sufficient to deny the If-Then constant any existence in the Explicate Order. Moreover, the Then term of any If-Then constant refers to something that has a certain degree of generality. Well, in the Explicate Order ( = space-time world) there exists nothing which ontologically stands on its own feet and has at the same time a certain degree of generality. So it is clear that If-Then constants as such do not reside in the Explicate Order. But they must reside somewhere, because they determine things (things, that is to say, in the Explicate Order). So they must reside in another sphere of Being, and this sphere is of course the Implicate Order (as described above). And thanks to the incessant dynamical 'interaction' (projection, injection) it is conceivable that a principle or category, and especially an If-Then constant, while itself residing in the Implicate Order, can nevertheless determine things in the Explicate Order.
How could we possibly conceive this act of determining things ?
Well, because all this, that is, If-Then constants and the Implicate Order, is just a hypothesis, we can only present a speculative description of this act of determination.
The Implicate Order is assumed to be a noëtic medium populated with noëtic contents or forms. As such it is more or less comparable with the domain of mathematical entities. There is no physical space and no physical time. The non-spatial nature of the Implicate Order brings with it that  distance  in the spatial sense is not defined in this Order. Here,  distance,  if present at all, is defined differently. And it should by now be evident that  distance  between the entities or inhabitants of the Implicate Order, which inhabitants are nothing more than mere contents or forms, is defined by the degree of similarity of their contents (formal distance). The distance between formally identical contents or forms is then obviously equal to zero.
Now when in the Explicate Order there is present (at one particular location) some (material) thing carrying a particular content or form, the latter can be carried into the Implicate Order by the above described process of injection. When in the Implicate Order there is already such a content or form present, the injected content or form will immediately merge with it :  they are formally identical, so their distance from each other is zero. Now the content or form originally already present in the Implicate Order could happen to be the If component of some If-Then constant residing, as all If-Then constants do, (exclusively) in the Implicate Order. And if now the injected content or form happens to be formally identical to one of the conditions as contained in the If component of the If-Then constant, then the latter is 'activated', which here means that the content of the constant's Then component, or a copy of it, will be projected into the Explicate Order. It will be unfolded along this Order's space and time dimensions, and in this way appearing in the space-time world. So the  injection  of a certain content or form into the Implicate Order is quickly followed by the  projection  of that what is contained in the Then component (or a copy of that) of the If-Then constant. Said differently, what we see happening in the Explicate Order, that is, in the space-time world, is the initial presence of some given content or form (always carried by an ontological substrate) followed by its  disappearance,  and, simultaneously with this disappearance, we see the  appearance  of something else, that is, the appearance of another content or form (carried by a substrate).
What we have described here is an ultimate unit or element of the causal process, and how such a causal element is based on the (ontological) application of a particular If-Then constant residing in the Implicate Order  to  some particular content or form existing in the Explicate Order and formally identical to one of the conditions contained in the If-Then constant's If component. In the earlier sections of this document such a unit of the causal process was depicted as a red line dynamically connecting two consecutive subsystem states. The production of such a subsystem state (which is always a part of a complete world state) from the previous one was seen to be based not on just one such connection but on many of them, as was depicted in Figure 5, which Figure we here once again give :

Figure 5 :  Two consecutive states (blue vertical lines) of a subsystem. The next state (i.e. the one on the right) is completely determined by the application (in an ontological sense) of several If-Then constants (red lines) having their antecedent in one state (i.e. the one on the left) and their consequent in the next state.

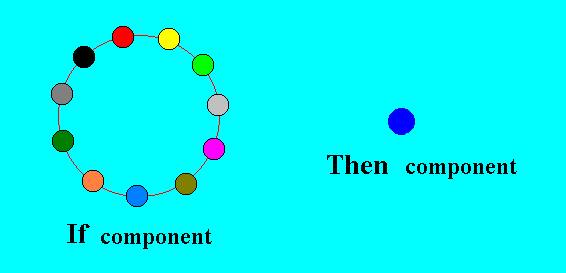
Figure 6 :  The If component and the Then component of an If-Then constant.
The If component (or, equivalently, If term) 'lists' the members of the set of all possible sufficient grounds (each one of them symbolized by a colored disc) for the existence in the Explicate Order of that for which the Then component (or, equivalently, Then term) stands. The possible sufficient grounds or conditions are 'listed' (in the If term) disjunctively (as in  "A, or B, or C, or, D, or ..." ).

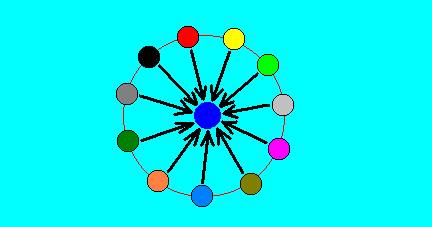
Figure 7 :  Scheme of an If-Then constant. The central blue disc symbolizes the Then component (or term) of the If-Then constant. The other colored discs (for clarity arranged along the circumference of a circle) symbolize the possible (different) sufficient grounds for the existence in the Explicate Order of that to which the Then term refers. The arrows symbolize the implicative relation between the If component and the Then component :  As soon as one (no matter which one) such sufficient ground (symbolized by one colored disc) exists in the Explicate order, that for which the Then term stands will appear in (that is, will be projected into) the Explicate Order.

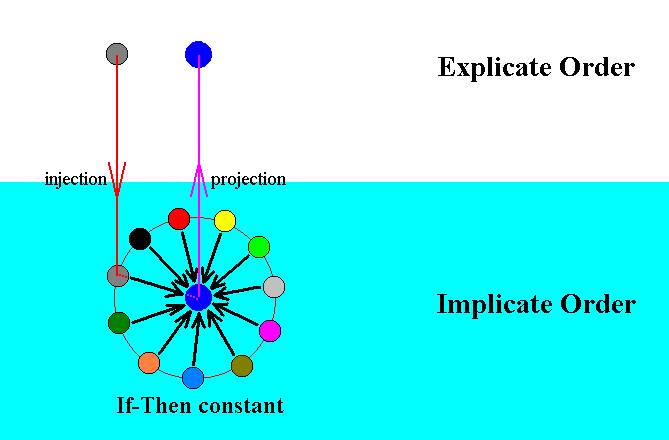
Figure 8 :  Activation of an If-Then constant.
One of the sufficient grounds or conditions, as listed by the If term of the constant, happens to exist in the Explicate Order. As a formal content it is then  injected  into the Implicate Order and  merges  there with the formal content of the corresponding sufficient ground as it is present in the If term's 'list', because these contents are formally identical. The If-Then constant is now activated, which here means that the formal content of the constant's Then term is  projected  into the Explicate Order and thus becoming spread out (that is, unfolded) along this Order's space and time dimensions.

Figure 9 :  The existence in the Explicate Order of something (grey disc) necessarily implies the existence in the Explicate Order of something else. What we see in fact is that an existing something disappears (it is injected) making place for the appearance (projection) of something else (blue disc).

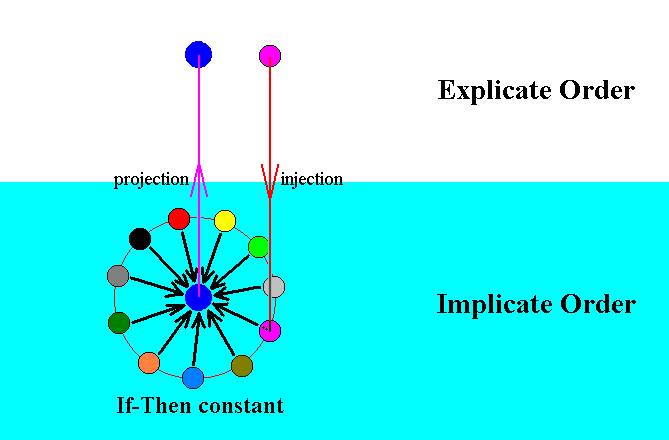
Figure 10.

And again, what we see in the Explicate Order is that the existence of something implies the existence of something else :

Figure 11.

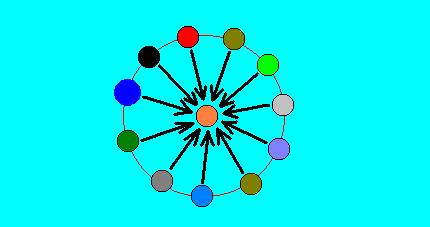
Figure 12 :  A second If-Then constant which in its 'list' of sufficient grounds happens to contain a sufficient ground (larger blue disc) that is qua formal content identical to the content of the Then term of the first If-Then constant. Although these two contents are formally identical and reside in the Implicate Order, they do not merge, because one represents a Then term while the other represents an If term. So there still is some 'noëtic distance' between them.

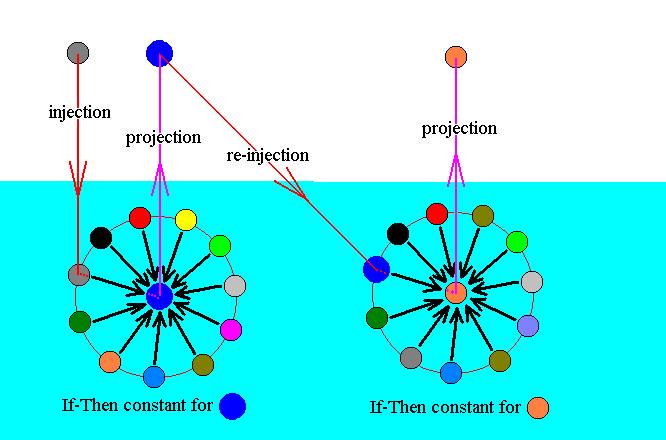
Figure 13 :  The two above discussed If-Then constants are coupled. The If term of the first If-Then constant implies, via its direct Then term, the Then term of the second If-Then constant.

Figure 14.

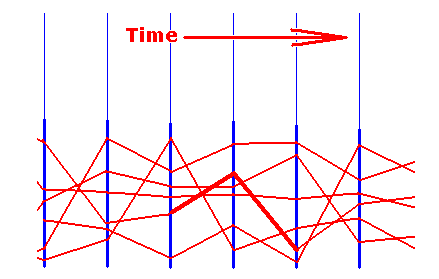
Figure 15 :  The successive application of the two If-Then constants considered above, seen in a broader dynamical context.
The vertical blue lines are the successive states of a dynamical system, that as subsystem is a part of the one complete world system. The thin extensions of the blue lines indicate that the states of the subsystem are just parts of the corresponding world states.
Every red line segment between two adjacent system states (blue lines) stands for the application of a particular If-Then constant. Two such red line segments, which are highlighted by being drawn as bold lines, and which are consecutive, stand for the successive application of the two above discussed If-Then constants.

Back to Homepage

Back to Contents

Back to Aristotelian metaphysics Part I

Back to Aristotelian metaphysics Part II

Back to Aristotelian metaphysics Part III

Back to Aristotelian metaphysics Part IIIa

Back to Aristotelian metaphysics Part IV

Back to Aristotelian metaphysics Part V

Back to Logic Part I

Back to Logic Part II

Back to Logic Part III

Back to Logic Part IV

Back to Logic Part V

Back to Logic Part VI

Back to Logic Part VII