e-mail : 

Back to Homepage

VEATCH deals extensively, that is, thoroughly, with the status of propositions from an intentional viewpoint and from that of the mathematical logicians. Much of it has been already dealt with by me in the document that was about the problems that had to be solved first and foremost, before even beginning to treat more systemativally of an intentional Logic.
So these particular problems will now be more or less skipped, or treated of only briefly. The main thrust was the distinction between real (and therefore) non-intentional relations and logical relations of identity, which are therefore intentional relations. That is to say, it was argued that the only type of logical proposition is the subject-predicate proposition, because only propositions of this type do genuinely intend anything. As has been said, this was already treated of earlier.
Among the new issues to be discussed here is the  theory of supposition (or designation),  which has its roots already deep down into the Middle Ages, and deals more or less with the same problems as are dealt with in quantification theory of modern mathematical Logic.

When we observe a thing that is presented to us (that is, to our senses) as (this thing) existing, we can ask what it is, and we answer with a subject-predicate proposition (S-P proposition). So the existence of the significatum of the subject is presupposed, and the existence of what the predicate signifies, that is the existence on or in that what the subject signifies, is asserted.
On the other hand, the existence of many things is not, and sometimes cannot, be given to us directly in sense experience. Accordingly, we may inquire concerning them as to whether they are or not. And to such a question the proper answer will quite naturally be in the form of an existence proposition. Such a proposition has the form  ' X is ',  or  ' X is existing ',  or  ' X is real ',  and as such may be considered true or false.

The whole structure of the S-P proposition, involving as it does the distinguishing of what is really one and the re-identification of what was never in fact two, is nothing but the work of reason, i.e., nothing but an ens rationis ( = a being of reason). At the same time, just as it is clear that both the distinction and the identity of the two terms in the proposition, S is P, are products of reason, still one would never maintain that the notion of S and the notion of P involve no difference in meaning.
In fact we can say that the S-P proposition intends entities that are formally distinct but materially one. For example, being a scotsman is never separated from te philosopher Hume :  Hume  is  a scotsman. Nevertheless  ' Hume '  and  ' scotsman '  do not have the same meaning  ( VEATCH, p.166 ).
In the proposition S is distinguished from P, but at the same time also identified in the same proposition. S is said to be P. The distinction of predicate from subject in a S-P proposition is based in the formal distinction in the thing. Materially, the thing is one, which fact is expressed by  ' is '  in the predication. While in our subject and predicate concepts we do take note of really different (ontological) parts or aspects of an ontologically composite being, we at the same time and in these same concepts connote the whole of which these parts are parts  ( VEATCH, p.168 ).
If a predicate signifies one of the ontological parts just as such, for instance a determination just as such (e.g., whiteness), or the Essence just as such (e.g., humanity), then it cannot be predicated of the whole, which is more than one of these parts. Nevertheless, if one's concept signifies such a part and at the same time connotes the whole of which it is a part, then predication is possible.
There are several main types of existential unities, that is, these are given from the outset. And these unities can be intended by subject-predicate propositions. The significatum of terms is not determined by their role in a proposition, that is, it is not so that their signification is only then determined when they figure in one or another proposition. Their signification is already determined by the Categories (that is, to what Category such terms belong). However, their  supposition  or  designation  (that is, to what part of their extension they now refer in a particular instance) is only determined by the propositional context  ( The theory of supposition [designation] will be further expounded below).
It is propositions that intend the mentioned existential unities (such as  Socrates-being-tanned,  Socrates-being-human,  etc.). And because there are several main types of such unities, there are several different main types of propositions to intend them, here :  (several different types of) subject-predicate propositions. These latter main types of predication are the Predicables.
In any S-P proposition, whether accidental or essential, subject and predicate both refer to the same essential whole, by signifying primarily one (ontological) part of that whole, and connoting the other part by way of connoting the whole complex, whereby 'connoting' is just a logical act, and no more than that. In this sense, and by connotation, both subject and predicate signify the same whole. And that's why they can be identified with each other in a proposition. Nevertheless, considering what the two concepts (subject and predicate) signify primarily and not connotatively, it is obvious that they signify different formal contents or essences.
So the type of existential whole determines how we should call the S-P proposition that intends this whole. In this way we interpret a given predication as either  accidental  or  per se,  and within te latter we distinguish several subtypes, that is, a  per se  predication is either a predication of  a  genus  (or  species ),  or a predication of  a  differentia,  or a predication of  a  proprium  (property). And these, viz., accidens, genus, species, differentia, and proprium, are the Predicables.
Because we have discussed the Predicables already many times on earlier occasions, it will suffice here to present only a few more elaborations on them.

There are several different types of entitative patterns existing in extramental reality, that can be intended by S-P propositions or concepts :

1. Essence-Supposit.  Example :  Socrates-being-a-human.

2. Substance-Accident.  Example :  Socrates-being-tanned.

3. Essence of a given substance.  Example :  humanity.

4. Essence of a given accident.  Example :  tannedness.

5. Unity of order.  Example :  Socrates-teaching-Plato.

(1) is an ontological unity that is  per se  one. It has a genuine Essence.
(2) is an ontological unity that is  per accidens  one. As such it does not have a genuine Essence.
(3) is an abstracted Essence of a substance, and as such is  per se  one.
(4) is an abstracted essence of an accident, and as such is  per se  one.
(5) is not an ontological unity, but several such unities. That is, it is not a subsistent entity, but several such entities. Such (subsisting) entities stand in a certain relation to each other, forming one or another unity of order. A unity of order is  per accidens  one. It does not have a genuine Essence. It is an aggregate.
It seems that there exist intermediates between (1) and (2) on the one hand, and (5) on the other, blurring the distinction between Substance and Aggregate. However, our dynamical systems approach (See First Part of Website )  will keep the distinction clear.

How, then, are those entitative patterns to be intended?

1. The entitative pattern  Essence-Supposit,  such as  Socrates-being-human,  can be intended by a subject-predicate proposition such as

   Socrates is a human being.

   The subject term  ' Socrates '  stands for the supposit ( = the given individual actually existing substance).
   The predicate term  ' a human being '  stands for the Essence that is in this supposit.
   The predicable relationship is that of  species  to individual ( =  per se  predication provided the subject term does not stand for a particular individual, but for an individual-as-example).

2. The entitative pattern of  Substance-Accident,  such as Socrates-tanned, or carpenter, or salesman, etc., can be intended by a subject-predicate proposition, such as

   Socrates is tanned, or

   Peter is a carpenter, or

   Harry is a salesman.

   The predicable relationship is that of an accident (accidens) of a subject ( = accidental predication).

3. The entitative pattern of  an Essence of a given individual substance, such as humanity, can be intended by a concept. And when we ask what it is, the answere to that question would be that concept's definition or part of its definition, for example :

   humanity is (rational) animality.

   The predicable relationship is that of  a  genus  (or  a  differentia )  of a definiendum. It is  a  per se  predication.
   When we go all the way up in the Category of Substance, the definition will be complete.

4. The entitative pattern of the  essence of a given accident,  such as tannedness, can be intended by a concept (expressed as an abstract term). And when we ask what it is, the answer to that question would be that concept's definition or a part of its definition, for example :

   tannedness (or tan) is the brownish color of the skin as a result of its exposure to sunlight.

   The predicable relationship is that of  a  genus  (or  a  differentia )  of a definiendum. It is  a  per se  predication.
   When we go all the way up in the relevant accidental Category (for tannedness that will be Quality), the definition will be complete.

5. The entitative pattern of  a  unity of order,  or aggregate, of individual substances related to each other in some way, for example  Socrates-being-a-teacher-of-Plato, can be intended by a subject-predicate proposition. But not without qualification :  While an accidental unity  ( (2) ),  such as  Socrates-tanned,  or  carpenter (that is, some human being who happens to have the skill of manipulating wood), is not one single essence, but is composed of two essences (humanity-tannedness, or humanity-carpentry), it is nevertheless one in supposit or existence. But  a  unity of order  not only is not one single essence, but is moreover not a subsistent entity at all (it is an aggregate of such entities). How, then, can it be intended by a subject-predicate proposition (where the subject should stand for an  ' it ',  that is, for a subsistent entity)?
   Well, such a way of intending is possible only if we treat such a unity of order as if it were a single subsistent entity, about which we then ask what it is, and answer with a subject-predicate proposition (where the predicate term stands for the what of that for which the subject term stands).
   So if we have to do with the unity of order as we see it for instance in :

   Socrates-Plato pattern, in which Socrates teaches Plato,

   then we can intend it in three ways, namely either by :

   This Socrates-Plato pattern  is  one of Socrates teaching  (that is, is an instance of Socrates-teaching. Socrates may be teaching many would-be philosophers, but in this particular instance he teaches Plato),

   where the predicable relationship is that of  species  to  individual,

   or (it can be intended) by :

   Socrates [subject]  is (was) [copula]  a teacher of Plato [predicate].

   where the predicable relationship is that  of  accident (accidens) of a subject. But now, by singling out one feature (namely Socrates) of this unity of order, we do not intend the whole unity in a subject term and then predicate something of it, but predicate something of one important component of this unity. As such it is then intended as a type (2) entitative pattern :  Substance-Accident,

   or (our unity of order can be intended) by :

   focussing on the very  relation  itself that connects the two members of this unity of order, namely the relation  teacher of.  Also in this case we do not intend the whole unity of order by a subject term and predicate something of it, but let the subject term intend only the relation. This relation can thus be intended by a concept. And when we ask what this relation  teacher of  is, we can get as answer a subject-predicate proposition, in which the predicate stands for the  definition,  or partial definition, of the relation  teacher of :

   teacher of  is  a relation of conveying knowledge.

   The predicable relationship is that of  a  genus  (or  differentia )  to a definiendum. It is  a  per se  predication.
   When we go all the way up in the Category of Relation, the definition will be complete.

The designation (as contrasted with the signification) of concepts is ultimately closely tied up with the propositional context in which these concepts find themselves. So it is in the present document, treating of the  Proposition  (as it is to be interpreted in intentional Logic), where we have to discuss the Theory of Designation.
Every concept has, when it is fully developed, a fixed meaning or signification  ( significatio ).  It can as such stand for every individual in its extension. However, when the concept figures in a proposition, the reference of the concept can, in some cases, get restricted, resulting in the concept to refer to only a part of its (natural) extension, dependent on the precise propositional context. Whether this context does or does not restrict the reference of the concept, we have in both cases to do with the  factual  (and therefore actual) meaning of the concept. In other words, while the concept  signifies  all individuals in its extension, it can, when finding itself in a certain propositional context,  designate  only a certain part of this extension.
We can, however, express this also a bit differently :
The concept  signifies  a definite formal content. This formal content is the concept's intension. On the basis of this, it can stand for all individuals of its (natural) extension, when that concept is taken all by itself, that is, it can stand for all individuals possessing in some way this formal content, and the total of these individuals then form the concept's natural extension. But in fact when we do let the concept stand for all individuals possessing this formal content, we disjunctively predicate the concept (intending that formal content) of each of these individuals. And this extension we can call the concept's full designation.
When, on the other hand, the concept finds itself in a propositional context, and this propositional context happens to restrict this full designation to just a part of the full extension, we have an instance of accidental designation of the concept.
This is, in a nut shell, the  theory of designation,  already known in the Middle Ages as the theory of supposition  ( suppositio ).

We will first discuss some inspirations derived from medieval ideas concerning  supposition  (also those ideas which boil down to rejecting  supposition  altogether), and then we will discuss VEATCH's updated version of it, which he calls the  theory of designation  (pp.193).

The above determinations can be made more exact by the following considerations :

Signification of a term (which is a concept [natural sign] linguistically expressed by a word or group of words [conventional sign] )  is the acquired comprehension of it, that is its formal content, which itself is one or another nature or essence. Meaning is here intensionally determined (in contrast to extensionally defined). This content is, on further occasions, brought back before the mind again as soon as the  word  is said, heard or read.

Designation (supposition) of a term, on the other hand, is its use, that is, its application to individuals of its extension, that is, to all or some individuals which possess the nature or essence determined by its signification. This application is expressed by the term's figuring in an implicit or explicit proposition, a sentence, or part of it.
Which individuals from the term's extension are designated depends on the sentential context of the term. Such a context can be determined by an adjective, such as in  ' white man '  :  Here the designation of the term  ' man '  is limited to men with a white skin, excluding all colored men. This is an example of a non-propositional context. There are more such contexts, between which we need not differentiate.

Natural designation (natural supposition) of a term is unlimited designation (unrestricted designation) :  The term, while signifying its content, has natural designation (which it can have as a natural ability in virtue of its signification) when it designates all actual and possible individuals possessing this content. It can do so, when the term is without context, or is taken without context, or when the context is such that it does not restrict the term's meaning (as in a definitional proposition).
So in this view natural designation of a term is identical to the full extension of the term.

REMARK :
We will, in all this, and with it in the whole of Logic as presented here, restrict ourselves to metaphysical and scientific contexts. We exclude all social and linguistic contexts, that is, we restrict ourselves to objects of theoretical knowledge, i.e., how they are intended by logical tools. For example, the designation (supposition) of the term  ' King '  in  ' the King '  is restricted to the king of the relevant country. Here the restricting context is social. And such cases as this one, we will not discuss, because we are not intended to develop a full (intentional) Logic covering all contexts, but only insofar as such a Logic informs us about metaphysics or science, not meaning that these latter are based on Logic (they're not), but meaning that finding the logical tools that are apparently being used by us in (theoretical) knowledge will inform us about the real constitution of things in extramental reality (or considered to be in such a reality).

So  signification  is the meaning of a term as  intensionally  determined. On the other hand, the  designation  (supposition) of a term is its  actual  meaning. It is actual because the signification is implicitly or explicitly applied to relevant individuals, and to apply to them is to predicate of them (disjunctively). In  designation  the meaning is therefore  extensionally  defined.
When the domain of extension is not restricted, and the meaning still extensionally defined, we have the case of  natural designation  (natural supposition). Restriction is brought about by the (syntactical) context of the term, although not all such contexts result in restriction, such as when the term figures in a definitional proposition, like  ' man is an animal '  (incomplete definition),  or  ' man is a rational animal '  (complete definition [but still not absolutely so] ).  Here the meaning of the term  ' man '  is not restricted. Most (syntactical) contexts, however, do restrict the domain of extension of the term.
Designation (supposition) of a term, whether natural designation (essential supposition) or not (accidental supposition), is always the  actual  meaning of the term, while signification is its  basic  meaning.

The following account on designation (supposition) is based on a chapter (Chapter 8) in Middeleeuwse wijsbegeerte, a book written (in Dutch) by L.M. de Rijk in 1981.
As far as I can detect, de RIJK adheres to a strictly extensional approach to Logic, that is, meanings of terms are defined extensionally, namely by pointing to the set, collection, or class, of individuals of which the meaning of the term can be predicated or applied. This means that he rejects any  intensional  interpretation of meaning, that is, meaning as formal content, essence, or nature. At least he rejects any fundamental status to be attributed to intensional meaning. Indeed, we can just  define  (with no further pretension) the meaning of a given concept (namely) by listing all the individuals that are supposed to belong to the extension of the concept. That is to say, we can just arbitrarily define such a meaning.
However, I think, that when our discourse is about the formal tools of knowledge, as it should be in Logic, we cannot just arbitrarily define the meaning of any concept that is about something in the objective world. That is, we cannot just stipulate which individuals do or do not belong to such a concept's extension. It is what a given individual thing or event is that must decide upon whether it should be included in the concept's extension or not. And so it seems that we cannot avoid to involve an intensional approach to meaning. Only after this is done, as it is in signification, we can speak about the concept's extension, and indicate the class of individuals, individuals, that is to say, of which (individuals) the content of the concept can be predicated.

De RIJK regrets that in medieval Logic one never was persuaded to drop  significatio,  in favor of  suppositio,  especially of natural supposition, that is, whatever one did with  suppositio,  one never abandoned  significatio.
But if  significatio  would have been dropped, then natural supposition would come into its place. But then the meaning of a term would be dependent on (syntactical) context, and this is in fact the Porphyrian reversal, rightly criticized by Ockham (See Logic Part I ).  The meaning of a term will, when doing so, be dependent on the truth of the proposition in which the term is used. Apparently, according to De RIJK, a term has no meaning at all when isolated from any context. The meaning of a concept becomes dependent on our discourse.
We have argued that this is a wrong approach (and a wrong interpretation of the Predicaments and Predicables). It is true, that a concept, as a sign with meaning, more or less gradually emerges as a result of repeated experiences, where the content (while it is building up) is predicated of existent individuals. But this predication is implicit, and as such it is not a proposition. This implicit predication is a part of the process of formation of the concept, not an application of a fully-fledged concept to one or more individuals.
Nevertheless De RIJK has given an interesting account of medieval theories of signification and supposition, and we will present some of the ideas considered in this account. Thereby our motivation is mainly thematic, not historic.

A complex term such as  ' white man '  clearly restricts the meaning of the  t e r m  ' man '  in this expression. The meaning of the  c o n c e p t  ' man '  as such is, of course, not restricted. It applies to all men.
Also the meaning of the  t e r m  ' white '  is restricted in the expression  ' white man '.  And also here the meaning of the  c o n c e p t  ' white '  as such is not restricted. It applies to all white things (while in the expression it only applies to all white men).
So here we see supposition -- here accidental supposition -- at work, not in a proposition, but in just an expression. This indicates that the actual meaning of a term is not necessarily determined by a propositional context. Especially, it is not necessarily determined by the truth of any proposition. But it could be, and often is, so determined (whereas the basic, or intensional, meaning [ = significatio] is by definition never determined by any [syntactical] context). The actual meaning of the  t e r m  ' man '  in  ' white man '  depends (according to me) first of all on its signification (significatio), which is the content or comprehension (or intension) of the  c o n c e p t  ' man '  as such. It is then restricted by the expression, resulting in the exclusion of all colored men. That is, when the term  ' man '  has natural supposition, it stands for -- designates -- all individuals (colored or white) that possess human nature (and the set of all these individuals forms the natural extension of the concept). When, however, the concept  ' man '  figures as the term  ' man '  in the expression  ' white man ',  it no longer designates all individuals possessing human nature, but designates only some and excludes others.
The same goes for the term  ' white ',  but here things are a bit more complicated.

In the case of a categorical proposition ( = assertion without any condition) insofar as it is (interpreted as) a subject-predicate proposition and as such being a predication,  it is the propositional context which determines the actual meaning of the terms of the proposition. And the  truth  of such a proposition depends on the actual meaning of its terms. Thus we have :

Signification ==>
propositional ( = syntactical) context ==> actual meaning (designation) ==> truth.

Things become even more clear when we consider a proposition that is evidently false :

man is an aerial being,

that is, man is an organism like a bird, a pterosaur, or a bat.
' Man '  signifies human nature. If this term has natural supposition, then it indicates, or stands for, all men, which comprises the concept's full extension. But this extension is contracted when the term  ' man '  figures in the above proposition, that is, its syntactical context restricts its meaning :  The term  ' man '  now does not stand for all individual men anymore, but only for those men that are aerial beings.
The same goes for the term  ' aerial being '.  This term signifies the capability of a living being to fly all by itself. When the term has natural supposition, then it indicates, or stands for, all individual beings (men, birds, etc.) that are aerial, which comprises the full extension of the concept. But the extension of also this concept  ' aerial being '  is contracted by the syntactical context :    ' Aerial being '  does not stand for all individual aerial beings anymore, but only for those that are (also) men.
So the actual meaning of the term  ' man '  in our above proposition is such that we can say that the term stands maybe for all, but at least for a number of individuals possessing human nature. And the actual meaning of the term  ' aerial being '  is such that the term stands, albeit not for all, for a number of individuals possessing a nature such that they have the ability to fly all by themselves ( NOTE 40 ).  And because the two natures, viz., human nature and a nature such as to be the ability to independently fly, that is, the two actual meanings, are not compatible, the proposition  ' man is an aerial being '  is false  ( Of course already the respective significations of the two concepts are mutually incompatible, but it is ultimately the actual meanings of the terms in the proposition that count for its truth or falsity).

In all this we could consider the position of Ferrer (1350-1419 A.D.), namely that we can only speak of supposition within and through a propositional (especially the S-P proposition) context (all non-propositional contexts are here supposed to be functional only within a proposition). Supposition is here said to refer to the actual meaning of a term when it is used as (grammatical) subject (suppositum) of a sentence. What precisely was the subject of the proposition, that is, what the proposition was about (id de quo sermo seritur [here the question expressed in present tense] )  becomes evident from the sentential connection, especially through the predicate used. The subject term now referring to its meaning as it is delimited by the predicate term, has supposition. And if the predicate does not restrict the intrinsic meaning -- as given by its significatio -- of the subject term, then this subject term has natural supposition. This is the case when the predicate expresses an essential property of the essence, or (part of) this essence itself, of the subject (that is, of that what is signified by the subject term).
The concept, also when it is expressed by a subject term, has (already) significatio apart from the term's relation to the predicate term, because significatio is already possessed by the concept, which (concept) we have when we take the corresponding term alone, without taking into consideration any relationship it might have (termino absolute considerato). In this way Ferrer (who was a 'realist', meaning that he finds it legitimate to consider abstract entities in extramental reality) could found scientific propositions. In such propositions the subject term has natural supposition, because the predicate expresses something essential of that what is referred to by the subject term.
The true nature of his natural supposition stands out when we consider one of his rules expressing how natural supposition functions. He says :  we cannot hold :  ' man is mortal, ergo man is '.  Of no proposition in which the subject term has natural supposition, applies as truth condition that those things for which the subject and predicate terms stand do exist. In other words the proposition  ' thunder is a sound in the clouds '  is also true when there is no cloud in the sky. The only truth condition is that subject and predicate essentially belong together. And existence, so he says, does not belong to the essence of things. The essential unity of subject and predicate is based on the formal contents involved, not on the concrete world (because then the essential unity would demand concrete existence). It also cannot be based on human thinking alone, because that would demand the concrete existence of men. Terms in natural supposition stand, according to Ferrer, for all times and for all relevant individuals. So this kind of natural supposition is atemporal.
On the other hand, for those, that is, for the Nominalists, who take serious te ground rule that nothing exists apart from concrete things, this assessment of a universal proposition (as such propositions figure in science) is hard to follow.
For the nominalists it was paramount to found knowledge, also scientific knowledge, on the world of concrete things, that is, existing things. They had to precisely indicate the relation between a language -- which apparently cannot go about without general terms -- and the World, which consists of individual beings only. As regards our special problem, the nominalists had to show that the truth of every proposition involving general terms, totally depends on the semantic relations of its terms to concrete individual beings. They held, namely, the general rule regulating truth, stating that a proposition is true only when its subject and predicate terms stand for the same concrete entity. When subject and predicate terms refer to different things or to something which, at the time of the enunciation of the proposition does not exist, the proposition is according to them false.
So in this view the interpretation of scientific propositions (as to their truth) as Ferrer had it, was clearly impossible. A nominalist cannot base this on abstract entities or formal contents, because for him all that exists are individual things. For example, with respect to the term  ' equality '  all there is are :  "equal sticks and equal stones". There is no such thing as equality.
The problem that certain demonstrative propositions posed for the nominalists, namely those demonstrative propositions whose subject term refers to things that do not exist at the time of the enunciation of the proposition, was not an easy one to solve for them. For everybody acknowledged, with Aristotle, that demonstrative propositions are necessarily true. And for the nominalist this means true at all times. How then handle the definition of  ' thunder '  when the weather is perfectly clear with no clouds at all? Especially when we take such a definition, not as a provisional agreement, but expressing the whatness as good as it can. The question was how the nominalist was able to found the character of necessity of a scientific proposition of which the significatum of the subject term was non-existent, in a world of contingent beings.
Ockham, as reported by De RIJK (p.251) had found an elegant solution. He said that all categorical demonstrative propositions are in fact superficial formulations of conditional propositions. So according to him the proposition  ' every human being is a sensitive being '  stands for :  ' if something is a human being, then it is a sensitive being ',  that is, if there exists now something which is a human being, then it is a sensitive being. Here, for the proposition to be true, the significatum of the subject term does not need to exist at the time of the enunciation of the proposition. But, I would add, the truth rests on the fact that the consequent ( = "[then] it is a sensitive being") is a part of the definition of the term  ' man '  (sensitive being = animal), so the truth of the proposition is in fact based on  A ==> A  ( [rational] animal ==> animal), implying that the truth is based on the definition after all, that is on the essence, which is an abstract entity (and a nominalist does not recognize abstract entities in extramental reality).
Other nominalists rejected Ockham's solution. They, namely, held that the truth, also of conditional propositions, can only be founded in the concrete world (and as we saw, Ockham's solution apparently involves abstract entities [not necessarily as such detected by the mentioned other nominalists] which he himself wanted to be eliminated from extramental reality).
One of these opponents was Buridanus (14th century). He thought to solve the problem by re-introducing the institute of natural supposition. The crucial point for him was of course the relation of necessary truth (in casu that of scientific propositions) to the contingent existence of the things we know. According to him, nouns (in contrast to verbs) refer (of course via their respective internalizations) indifferently to things whether they exist presently, in the past, or in the future. That is, nouns are omnitemporal ("omnitemporal" here represents an extensional [denotative] approach to meaning, while "atemporal" [as we saw it in Ferrer] represents an intensional approach to meaning). In this way Buridanus thought to be able to found scientific propositions. According to him they are not pronouncing things with respect to a certain time, but to all times. The terms of such propositions  stand for  (supponunt) all individual beings that are referred to by them in virtue of their meaning, regardless of the actual point in time of the existence of those individuals. This point in time can lie in the past or in the future as well as in the present. This is the natural supposition of subject terms in scientific propositions.
I would like to comment on this.

Something that existed in the past, or will exist in the future, is not concrete (anymore). And the nominalists want to found knowledge on the concrete world.
With respect to the past we can say :  There existed all kinds of individual things. Now we must ask :  Which of these things must be subsumed under the supposition about which we are presently speaking? That is, which of those past individual things were such that they can be designated by the term we are presently using in a proposition? This can only be done on the basis of the supposed  nature  or essence of those (past) things, because stipulatively selecting them is not possible anymore. So when an object does no longer exist, the supposition (suppositio) must be based on a (supposed) essence or nature, for example as expressed by a definition. This means that the approach in this case has become an intensional one, because an extensional approach (selecting of individuals) is not possible (anymore).

So Buridanus wishes, in the case of scientific propositions, to speak of a natural supposition of terms. A term has natural supposition, so he says, when it stands for all its concrete individuals (supposita), whether they exist at the moment the proposition is enunciated, or only some time before it, or after it. In this way also the terms in a scientific proposition directly refer to concreta.

A 14th century critique against Buridanus's solution runs as follows :
Buridanus does something which is superfluous. His natural supposition doesn't serve anything. When he argues that he needs natural supposition to support the necessary truth of propositions like  ' every triangle has three angles making up 180⁰ ',  this critique answers him :  Once this truth is established of one particular triangle, it remains valid, because later assertions of this kind are already implied in the first.
It is interesting to note that this latter statement (about the implication of later propositions by the initially enunciated proposition) is analogous to the presupposition of a Species-Individuum Structure in things, making it possible to generalize one (or several) particular finding  ( We could say that because of this state of affairs in things we can repeat certain propositions about them). Once the property of 180⁰ of the angles is found in one particular triangle, it can be generalized over all triangles. But, I would retort, while this generalizing certainly takes place (legitimately) in the practise of natural science, in the present case we are speaking about mathematicals, and it is clear that in mathematics a particular triangle, here and now, that is, a totally determined triangle, is never as such the object of a mathematical enquiry. What the enquiry is about is  ' triangularity ',  which is a formal content, and from this formal content certain necessary properties can be deduced, without recourse to individuals (which, moreover, do not exist in mathematics).
So instead of the above example it would have been better to take one from material reality.
Let's consider the proposition  ' man is rational '.  This is clearly a generalization of a result that was obtained in only a limited number of individual instances. In this way the proposition automatically implies it to be legitimately made in the future (and in the past for that matter). So a scientific proposition is, according to this 14th century critique against Buridanus, not as such a proposition in which the subject term has natural supposition, here meaning that the supposition is omnitemporal, but a proposition about an object existing at the time of the enunciation of the proposition, while, at the same time, all future (and now also past) statements of this kind are implied by this one proposition.
One sees, this critique is not really a devastating one against Buridanus. The latter's doctrine of natural supposition is extensional-syntactical, that is, a term in a universal proposition, stands for all individuals of its extension, and so has natural supposition. Other syntactical contexts may restrict the reference of the term to just a certain part of its (full) extension. I do not know what then significatio meant for Buridanus. Generally, significatio is intensionally characterized, but such a procedure would be unacceptable for Buridanus as a nominalist, because then an appeal has to be made to some nature or essence residing in things.
The doctrine of natural supposition is different again in John of St Thomas (1589-1644). He distinguishes supposition, and thus also natural supposition, from significatio, by the fact that the former is about the use of a term for something for which it is verified in the proposition, while the significatio of a term is its meaning apart from any propositional context.
Just as for Ferrer (and Buridanus), his major problem is that of propositions in which 'eternal truths' are asserted. John says that their truth is not demonstrated on the basis of the findings in a sensible entity, but on the basis of an intelligible content, because, so he says, such a proposition is verified "according to the existence expressed by a verb that does not refer to a certain [particular] time". For example, consider a proposition like  ' Petrus is a human being'  (by "Petrus" is, as was often the case, meant the Apostle, otherwise there would be no problem). The term ' Petrus '  here stands for Petrus as atemporal essence (and that was, is, and will be, human nature). The propositional context is, according to John, strictly demanded. So the semantic model consists in the interpretation of the logical copula  ( ' is ' )  as referring to an 'atemporal existence'.
We could add :  An individuum is not atemporal, but the Essence in Petrus, namely  humanity,  is, and consequently the proposition is equivalent to  ' humanity  is  humanity '  (or also :  ' man  is  man ' ).  So if the Essence of Petrus is  humanity,  then the proposition  ' Petrus is a human being'  is necessarily true.
It is clear that the approach of John of St Thomas as regards natural supposition, is intensional rather than extensional. And the only difference with significatio (which is also intensional) is that we only speak of supposition (suppositio) (and thus also of natural supposition) of a term when this term is actually used in a proposition. So suppositio is in fact an operational approach to (the) meaning (of a term), in contrast to significatio. But then, I would add, this (operational) approach should at the same time be extensional, that is, an approach being about of which individuals the term is actually predicable when finding itself in some syntactical context ( NOTE 41 ).

From all this it is clear that there are many views concerning the status of supposition (suppositio). Very important is to distinguish between an intensional and extensional approach with respect to a theory of meaning (of terms).
The  comprehension  of a (given) concept (which in a proposition is represented by a term [itself represented by a word] ) ( NOTE 42 )  is understood to be the content (intension) of that concept, that is, the sum of the notions a term (representing that concept) evokes, and of which the best expression is the  definition  of the term representing the concept.
The  denotation  is the scope (extension) of the concept, that is, the sum of the things to which the content of the concept applies.
Relationally expressed :  Intension is a relation of a term to its content, while denotation (extension) is the relation of a term to the concreta ( = individual things) which are referred to by it.

We see, that not only of course in the intension of a concept, but also in the extension of it, we need the  content  of the concept.
So where we do not arbitrarily define concepts, but try to indicate to what the concept refers naturally, we need its content. This means that we cannot do without the significatio of a concept or term, that is, its natural meaning.

This concludes our preliminary discussion about suppositio. It can serve as a preparatory background for the ensuing discussion of Veatch's revision of the theory of suppositio and the use of it for solving some logical problems (for instance that of the null class).

After having prepared ourselves for discussing  supposition,  we will now plunge into Veatch's revised theory of supposition of terms in propositions.
In order to distinguish his theory from the older ones, he uses the term  ' designation '  rather than  ' supposition '.  Indeed, I think,  ' designation '  is the more appropriate expression.
My study of his theory is not aimed at a precise presentation of his views, but, helped by these views, to set up a more or less definitive theory of supposition or designation, which in effect is Veatch's theory, but then amended by me here and there. However, I will study it only inso far as it has bearing on metaphysics.

The introduction to the theory of designation, and the necessity for an intentinional Logic of having such a theory, is so well expressed and explained by VEATCH, that we cannot do better than to present his introductory exposition, as he has it at p.193-196, almost litterally :

So far the whole discussion [VEATCH having not yet mentioned the theory of designation] of the proposition has been directed toward showing (1) that the function of the proposition in an intentional Logic is the intention of existence, and (2) that the proper instrument for the performance of such a function is a proposition of the familiar two-term, subject-predicate structure, exhibiting the peculiarly logical or intentional relation of identity.
Unfortunately, however, no matter how plausible this discussion may have seemed as it proceeded, neither of these two theses can ultimately sustain itself merely on the basis of the evidence which I have cited so far. To see how readily both of them might seem to weaken and falter, one has but to fall back into those ingrained habits of thought with which almost everyone nowadays, Aristotelians and mathematical logicians alike, tends to view ordinary subject-predicate propositions. No sooner does one begin again to look upon subject-predicate propositions in this accustomed manner than almost immediately it would seem that such propositions neither intend existence nor involve a relation of identity.
For instance, a subject-predicate proposition must certainly involve two concepts, unless, that is, one has only a trivially identical proposition of the form S is S. But then if one's concepts are really two different concepts, they will most certainly have two different meanings, since concepts considered as formal signs are nothing but meanings. However, if the two concepts have two different meanings, one could not possibly say that they mean the same thing or are related by a relation of identity.
Instead, the much more sensible way of viewing the relation between the two terms of a subject-predicate proposition would seem to be those suggested by LEWIS in the following quotation :

In dealing with the logic of terms in propositions, either of two interpretations may frequently be chosen :  the proposition may be taken as asserting a relation between the concepts which the terms connote, or between the classes which the terms denote. Thus "All men are mortal" may be taken to mean "The concept 'man' includes or implies the concept 'mortal'" or it may be taken to mean "The class of men is contained in the class of mortals." The laws governing the relations of concepts constitute the logic of the connotation or intension of terms. Those governing the relation of classes constitute the logic of the denotation or extension of terms.

Yet why suppose that the terms which enter into a proposition are to be considered or compared simply with respect to their meanings? After all, such a comparison is already possible between concepts considered simply in themselves and quite apart from any role which they may play in a proposition. Accordingly, is it not conceivable and even probable that when they enter into a proposition, concepts come to acquire further properties which, considered just in themselves and as concepts, they do not have at all?
Specifically, what I am proposing is that when concepts enter into a proposition, in addition to  signifying  the natures and essences, and, on the basis of this, bring into their (natural) extension all individuals which have such a nature, they also come to  designate  certain things as being or existing.
Moreover, it is precisely in virtue of this property of designation which concepts come to have only insofar as they enter into a proposition -- it is in virtue of this property, I think, that I can now proceed to justify further my contentions that propositions intend existence and intend it through a relation of identity between subject and predicate.
For instance, in the proposition "All men are mortal", it is certainly true to say that the subject in this proposition, considered just as a concept, does not mean the same thing as the predicate. At the same time, considered just in itself, each of these concepts is simply a relation of identity between the abstracted essence which it signifies and the individuals in its extension. Nevertheless, in this proposition the subject concept "man" is used in such a way as to designate the items in its extension as existing in some sense or other, since it is they that are said  to be  mortal. And the predicate concept "mortal" is used in such a way as to designate as existing, precisely the same individuals as the subject concept does. In other words, even though subject and predicate mean different things, they are nevertheless both of them so used in the proposition as to designate exactly the same things as being or existing. And it is in virtue of this that the predicate can be  i d e n t i f i e d  with the subject.

some men are wise.

The signification of the term  ' men '  is, of course, still, human nature (explicitly given by its definition). But here in this proposition the significative content human nature can only be applied to a part of the concept's extension, that is, only to a limited number of individuals possessing this content, while excluding others, in spite of their also possessing that content  ( Here all non-wise men are excluded from the concept's natural extension). So the term  ' men '  in the proposition  ' some men are wise '  designates only a part of the concept's natural extension.

a man is entering the drugstore.

Also here the term  ' man '  signifies human nature. However, it designates only a single individual having this nature.
Now consider these two propositions :

the robbers fled to cover.

the robbers numbered five in all.

The signification of the term  ' robbers '  is given by the definition of the concept.
In both propositions the subject term applies this same signification to a number of individuals (and these are precisely those individual robbers that are relevant in the present context [which context is determined by the proposition] ).  That is, the subject term  ' robbers '  has exactly the same meaning or significance in the two cases. Yet so far as designation is concerned, what the subject term in the second proposition designates are a number of existing individuals taken collectively, whereas in the first proposition these individuals are designated as existing not collectively but distributively (See also further below, where more is said about the different kinds of designation).

But having understood all this, one might raise a question of this sort :
If designation means the use or employment of a concept to stand for something existing, then what about a false proposition? Do the terms that compose it designate anything, i.e., do they stand for any existing thing? To be sure, they do have meaning, since the falsity of a proposition by no means implies that its terms have no significance. Yet with designation it might seem to be different. For how in a false proposition could one be said to designate anything that is or that exists? Well, there can still be designated things that actually exist or have existed, in false propositions, because in many cases the falsity does not come from a failure of designation (of the subject term), but because the predicate simply does not match with the subject. So, for example, in  ' the Nazis captured Stalingrad ',  where the term  ' Nazis '  stands for things, individuals, that really existed. Nevertheless the proposition is false.
Now consider the proposition

the democracy of ancient Athens is ruthlessly imperialistic.

Here the subject term fails to designate anything, because at present there isn't such a democracy in Athens (as it is demanded by the copula  ' is '  [present tense] ).  Nevertheless the predicate is perfectly compatible with the subject :  Indeed, being ruthlessly imperialistic was certainly true of the ancient Athenian democracy. Here we can say that we have to do with a failure of the intended designation as determined by the copula of the proposition. The true designation turns out to be just a being of reason, that is, what is actually designated by the subject term is a mere being of reason rather than a real -- potential or actual -- being. Or perhaps the true designation is a possible being in extramental reality.
Anyway, it is the discrepancy between intended and true designation (actual real individual  versus  being of reason, or actual real individual  versus  potential real individual) that renders the proposition false.

The designation of a term in a proposition always refers to all or some existing individuals in the concept's natural extension. So it is to be expected that there are at least as many kinds of designation as there are kinds of existence. The existence can be actual and in extramental reality, such as it is designated in  ' a wolf was encountered in Oregon ' ,  or it can be possible and in extramental reality, and as such it is designated in the proposition  ' dinosaurs are reptiles ',  or in  ' a dinosaur is presently encountered while eating leaves from trees in Yoshemite national park '  if this latter proposition is false, that is, if it is false then, although actual existence was meant, it turned out to be only possible existence (the existence is actual when the proposition is true). The existence can also be a mere existence in the mind as in the proposition  ' a concept is an instrument of knowledge '.  Indeed, a concept can only exist in the mind. So the term  ' concept '  designates things which exist only as beings of reason, as VEATCH states on p.201. However, we must reflect upon how things are here with respect to the difference between signification and designation. Thereby we must not forget that signification is intensional, while designation is extensional. So we can say that here the term  ' concept '  signifies precisely that which is stated in its proper definition. And this is some formal content. What then is the designation of the term  ' concept '  in the proposition  ' a concept is an instrument of knowledge ' ? Well, the designation is the total of all individual states of mind to which that formal content applies.
Now consider the proposition

the concept of  ' man '  is a universal concept

Here also, of course, the signification of the term  ' the concept of man '  is its definition. This definition is not the same as the definition of the term  ' man ',  which is rational animal. Let us restate this more precisely :

The signification of the (subject) term  ' the concept of man '  is the definition of the concept  ' the concept of man '.  And this definition reads :  A simple (in contrast to composed) logical intention, intending human nature.
The designation of the subject term  ' the concept of man '  in the proposition  ' the concept of man is a universal concept '  is all the individual mental states to which the just mentioned definition can be applied.
So here we accurately distinguish between the intensionality of signification, and the extensionality of designation, a distinction not always observed (or acknowledged) by VEATCH.

Now consider the proposition  ' man has inhabited the planet Earth since the end of the Miocene period '.  The concept  ' man '  signifies human nature, and perforce its definition (as formal content), while it designates (now as a term in the above proposition) all actual and possible existent men in extramental reality.

A  being of reason  is just an object before the mind, that is, an object only insofar as it is brought before the mind. Such an object is, for example, the concept  ' man '  (but, of course, also the concept  ' the concept of man ' ).  This object is an individual state of mind (or a decodable content in the brain) :  It can be repeated in the same mind or in different minds. Insofar as the concept  ' man '  is a particular state of mind, that state is not its meaning, but an item in its extension. The meaning or significatio of the concept  ' man '  is, as has been said, its definition. Its full extension is :  all the possibly or actually existing human individuals and (in addition to it) all the possible or actual individual states of mind to which that definition is applicable. The concept of  ' man ',  of which we now have indicated its extension, can be the subject term in a proposition, and this proposition decides whether this subject term designates individuals in extramental reality, if so, we can then express the subject term as  ' man ',  or (whether the subject term designates) individual states of mind. And if the latter, we must express the subject term as  ' the concept of man '.
As a possibly or actually existing material individual, man is a real being.
As a possible or actual state of mind, it is a being of reason.
However, we have a difficulty here.
If we want to include, in addition to real beings, beings of reason into the possible extension of a concept (in order to be able to cope with the problem of the null class below), then we view the concept itself as one of its designata. Is this permissible?  ( VEATCH has not seen this problem).
I think it is.
As I said, the designata of a concept consist of individuals or individual states to which its signification is applicable. This signification is some formal content (expressed in the definition). And indeed, this formal content can, not only be predicated of the real beings which possess this content, but also can be predicated of itself :  rational animal  is  rational animal. So indeed, the formal content, as it is a particular mental state, is one of the many legitimate and possible designata of the concept in question. As such a designatum it is not a real being but only a being of reason, but a being nonetheless.
Let us elaborate on this difficult issue a little more.
A concept is a (formal) sign which points to a certain formal content. This is its signification. Therefore it can stand for individuals having this content. When it stands for all of such individuals it designates universally, or, equivalently, it has natural supposition. These individuals are first of all extramental things. But also certain states of the brain carry this same formal content. So also these brain states are individuals or items in the concept's maximal extension. If the concept of, say,  ' man '  designates  e x c l u s i v e l y  these (corresponding) brain states, then the concept of  ' man '  is taken insofar as it is a  c o n c e p t  of  ' man ',  which fact is then expressed (in a proposition), not as the term  ' man ',  but as the term  ' the concept of man '.  This latter term designates all the individual brain states that carry the content  rational animal.
This result is necessary for the ensuing discussion of the problem of the so-called null class and of the existential import of all genuine propositions. A genuine proposition must always be about something that exists in some way or another, otherwise the proposition is not about anything at all, which means that it is not a proposition at all, and is consequently neither true nor false. So a proposition always must have existential import (which is, by the way, its distinction from a mere concept). But problems with the null class (as in the [alleged] proposition  ' the present king of France is bald ',  where there is no present king of France, or in the [alleged] proposition  ' all sea serpents live in the Atlantic ',  while we know that sea serpents do not exist at all)  have persuaded mathematical logicians to deny existential import of all universal propositions (while still admitting it for particular and singular propositions). And because the existential import of all propositions is a basic tenet of intentinal Logic, we must deal with the null class from an intentional point of view. For this we must admit to (reside in) the extension of a concept not only real beings (of which the concept's content can be predicated), but also beings of reason, because there are cases (within the problem of the null class) in which subject terms do neither designate actual existents nor possible existents in extramental reality. And in order for them not, for that reasom, to fail completely in designation, we must allow beings of reason in the domain of designata.
Of course, when a given proposition completely fixes the designation of its subject term, and when, at the same time, this designation cannot, however, be realized, the failure of designation is complete. In that case the proposition is either false or is not a proposition at all.
All this we will extensively discuss in the ensuing Section on the null class. The evocation of beings of reason serves for us to be able to insist that a proposition must always be about something existing in some way or another, otherwise it is not distinguishable from a mere concept, and is neither true nor false.

VEATCH, p.202, distinguishes between  inclusive  and  exclusive  designation. This, however, is, according to me, not correct. To illustrate this distinction VEATCH considers the following three propositions :

man is a universal concept,

the reptile is a division of the animal kingdom,

and

the opossum is a faunal section of North America
( I have slightly changed this last proposition to illustrate VEATCH's position better).

While in propositions like  ' all men are mortal '  the subject term designates individuals in extramental reality, the subject terms of the three above propositions do not designate respectively individual men, individual reptiles, or individual opossums all in extramental reality, that is, we cannot say :  ' this man is a universal concept ',  neither can we say :  ' this reptile is a division of the animal kingdom ',  nor, finally, can we say :  ' this opossum is a faunal section of North America '.  VEATCH in effect says that this is so because the subject terms in the above three propositions  signify,  it is true, respectively human nature, reptile nature, and opossum nature, as actually existing in extramental reality, but that they  designate  only beings of reason. Therefore we cannot predicate the respective predicate terms of actually existing (in extramental reality) individuals. This is correct. But what is not, I think, correct is that he calls this  exclusive designation,  that is a designation excluding individuals, because designation excluding individuals is not extensional, and by consequence not designation.
To resolve this problem we need only to state the three propositions more adequately :

the concept of man is a universal concept,

the class of reptiles is a division of the animal kingdom,

and

the class (taxonomically the species) of opossum is a faunal section of North America.

And now the apparent exclusion of individuals vanishes :
The term  ' the concept of man '  refers to all individual states of mind such that such a state is a formal sign of human nature.
The term  ' the class of reptiles '  is the result of a mentally grouping together of certain animals. It refers to all individual cases of such mentally grouping together.
The term  ' the class (species) of opossum '  is the result of a mentally grouping together of certain animals. It refers to all individual cases of such mentally grouping together.
All these are individual states of minds, and thus (the relevant) individuals (that is, the individual brain states carrying the relevant content) are not excluded :
The concept  ' the concept of man '  signifies its definition (which is a state of mind such that human nature is intended).
In the proposition  ' the concept of man is a universal concept '  it designates all the individual states of mind that intend human nature and (it designates) nothing else (while the concept  ' man '  in  ' man is mortal '  designates (all) individuals possessing human nature, individuals that is, existing in extramental reality [because "mortal" refers to the death, not of human nature, but to the death of extramental individuals having this nature] ).
The concept  ' the class of reptiles '  signifies the mental grouping of certain animals.
In the proposition  ' the class of reptiles is a division of the animal kingdom '  it designates all the individual cases of such a mental grouping of certain animals.
The concept  ' the class (species) of opossum '  signifies the mental grouping of certain animals.
In the proposition  ' the class (species) of opossum is a faunal section of North America '  it designates all the individual cases of such a mental grouping of certain animals.
Although looking awkward and cumbersome, this interpretation is, according to me, correct.
In this way a term like  ' reptile '  can either designate actually or potentially existing individuals in extramental reality, or it can designate certain individual states of mind, but then the term  ' reptile '  designates as  the concept of reptile,  the idea of reptile,  or,  the fiction of reptile  for that matter.
So when we have a proposition like  ' all sea serpents live in the Atlantic ',  and if this proposition is not pronounced in the context of a phantasy world (say in a novel), then we can say that the intended designation of the subject term  ' sea serpents '  are actual individuals existing in extramental reality, while the true designation is in fact that of the  idea of sea serpents  (that is, 'sea serpents' turned out to be merely an idea, or being of reason) which idea occurs as individual states of mind in individual minds. And because of this discrepancy between intended designation and true designation the proposition is false.
To illustrate matters further, consider the following syllogism or argument :

Animal is a genus,
I am an animal,
Therefore, I am a genus.

This conclusion is absurd. However, it does not follow from the premises, because there is in fact no middle term. We see this as soon as we reformulate the first premise rendering it correct :

The concept animal is a genus.

And now the alleged argument doesn't have a middle term anymore.

The above interpretation of the designation of terms like  ' the concept of man '  derives from our insistence that designation must always be extensional (in order that it be distinct from signification). Only then it can be restricted by certain syntactical contexts :  then certain individuals of the full extension are excluded, as we have it, mutatis mutandis in  ' white men '  designating, it is true, individuals possessing human nature, but excluding all colored individuals.

And now we see that there are several kinds of designation inasmuch either all existing individuals possessing that nature are designated by the term, or just some of them, or only a single one of them (as dictated by the syntactical context of the term). And these varying amounts of extension may in turn be designated in various ways.
Accordingly, let us undertake to give a more exhaustive account of these varieties of designation.
First we have :

• Singular designation, that is, designation in which the concept or term applies to only a single individual from the concept's natural ( = maximal) extension, e.g. (the single designation) of  ' tree '  in the proposition  ' that tree is deciduous '.

• Common designation, that is, designation in which the concept or term is thought of as applying not just to a single existing individual of the concept's natural extension, but rather to several of them or all of them (of the concept's natural extension).

• Universal designation.  This kind of designation we have already met as natural supposition. Here all the individuals of the concept's natural ( = maximal) extension are designated. For instance :   ' tree '  has universal designation in the proposition  ' all trees are plants '.
  But VEATCH, p.206, also calls the designation of the subject term in the proposition  ' the men in the plane were five in all '  universal (and collective) designation. This is correct. The subject term here is not  ' men ',  but  ' the men in the plane '.  So here 'universal' must refer to  ' the men in the plane '  rather than to  ' men '.  The designation of  ' men '  is contracted by the expression  ' in the plane '.  But this being so, our new 'universe' is now the plane, and the proposition is about all men in that plane, rendering the designation of the subject term universal.
  We can also express all this in a somewhat different and alternative fashion, which is worthwhile to think about :
  In the proposition  ' the men in the plane were five in all '  the term  ' men '  is the subject. What, then is its designation? Well, the maximal extension of the concept  ' men '  (or  ' man '  for that matter) is contracted by the expression  ' in the plane '.  As such we have a case of particular rather than universal designation. But -- the designation being so contracted -- we now have a new 'universe', namely the plane. And the proposition  ' the men in the plane were five in all '  is about all men in that universe. So the designation of the subject term  ' men '  is here universal after all.
  The term  ' men '  would naturally and clearly have universal designation in a proposition like  ' all men are mortal ',  and this kind of universal designation, namely covering the whole extension of the concept  ' men ',  is natural supposition or natural designation (as such not considered by VEATCH, because he amalgamates, that is, identifies, natural supposition and significatio, which we do not do, because we sharply distinguish between the intensionality of signification and the extensionality of designation or supposition).
  So again, in the proposition  ' the men in the plane were five in all '  the expression  ' in the plane '  restricts the designation of the term  ' men '  to these five individuals only. So in this proposition we must turn our attention to the term  ' the men in the plane '  (rather than to  ' men ' ),  because this term can now be considered to be the subject term of the proposition, that is, the subject term fully describing that for which it is supposed to stand, namely  "the men in the plane". And because the proposition is about all these men (here collectively so), the designation of the subject term  ' the men in the plane '  is universal (and collective).
  The same goes for  ' the men in the plane were all americans '.  Here the subject term  ' the men in the plane '  also designates universally, but now distributively so.

• Particular designation.  Here only some of the individuals of the concept's (maximal, natural) extension are designated. We recognize this as accidental supposition, or supposition by restriction. For instance  ' tree '  has particular designation in the proposition  ' some trees are obstructing my view of the scene ',  or,  ' some trees carry needles '.

Universal designation can be further divided into :

• Collective designation,  as for the term  ' robbers '  in  ' the robbers numbered five in all '.  The robbers are collectively designated. Or for the term  ' angles of a triangle '  in  ' the (interior) angles of a triangle are equal to two right angles '.  The angles are collectively designated. It is definitively not so that each (interior) angle of a triangle is equal to two right angles.

• Distributive designation.  As for the term  ' robbers '  in  ' the robbers fled to cover '.  The robbers are distributively designated. Or for the term  ' the angles of a triangle '  in  ' the angles of a triangle are those formed by the intersections of the sides '.  The angles are distributively designated. Each angle of a triangle is formed by the intersection of (two) sides.

• Determinate designation, as for the term  ' trees '  in  ' some trees grow in the tropics '.  The term  ' trees '  is here used to designate certain particular trees, i.e. trees having a particular nature (different from that of other trees).

• Indeterminate designation, as for the term  ' trees '  in  ' some trees are needed to break this barren landscape '.  Here the term  ' trees '  has (also) a particular designation, but it is wholly indeterminate which trees are meant.

every chair in this room is a straight chair,

we can infer the following conjunction of singular propositions :

this chair in this room is a straight one, and that chair in this room is a straight one, and that chair in this room is a straight one, and...,   and so enumerating every item in the extension of  ' chair in this room '.

This is an instance of descent.
On the other hand we can, given this conjunction of singular propositions, each one of them being about yet another item in the extension of  ' chair in this room ',  infer the universal proposition  ' every chair in this room is a straight chair '.  This is an instance of ascent.

Such being a description of what  ascent  and  descent  generally are, it now remains to consider the different kinds of ascent and descent corresponding to the different kinds of designation that attach to the terms from which the  descent  is made, or  to  which the   ascent  is made. In the case of terms whose designation in a given proposition is either  universal  and  distributive,  or  particular  and  determinate,  the descent always involves passing from one proposition that is more universal to a series of propositions that are less universal or to singular propositions. And when we do so in the case of a term that has universal and distributive designation, the descent is made to a series of propositions that are  conjoined  to one another by  "and"  (and so making up the series), while in the case of terms having particular and determinate designation, the descent is from a more universal proposition to a series of less universal propositions, or to a series of singular propositions,  disjoined  from one another by  "or"  (and so making up the series).
For example, take the universal proposition :

every hydrogen atom has a single proton.

Here the subject term has universal and distributive designation. Accordingly, the descent is from this as a universal proposition  to  a whole series of singular (and, therefore, a fortiori, less universal) propositions conjoined by  "and",  e.g.,

this atom of hydrogen has a single proton, and that atom of hydrogen has a single proton, and that atom of hydrogen has a single proton, and ...,   listing all the items in the extension of the concept  ' atom of hydrogen '.

On the other hand, in a particular proposition such as

some book from the library was lying on the dining room table,

the designation of the subject term  ' book from the library '  is particular (because of  ' some ' ),  that is, particular within the extension of the expression  ' book from the library ',  and determinate (because this book is not just any book from the library, but a certain definite one). Accordingly, the descent is from this as a particular proposition  to  a series of singular propositions disjoined by  "or",  e.g.,

it was this book from the library that was lying on the dining room table, or it was that book from the library that was lying on the dining room table, or it was that book from the library that was lying on the dining room table, or it was that one, or ...   listing all the items in the extension of the expression  ' book from the library '.

What now of ascent to, or descent from, propositions involving terms whose designation is not universal and distributive, but rather universal and collective, or terms whose designation is particular and indeterminate rather than particular and determinate?
The answer is that in such cases ascent does not involve a passage from less universal to more universal propositions. Nor does descent involve a passage from a more universal proposition to a series of less universal propositions.
Let us illustrate.
For example in the proposition

the men in the plane were five in all,

the subject term  ' the men in the plane '  has universal and collective designation. Clearly in such a case one cannot descend from this proposition to a series of less universal propositions such as

this man in the plane was five in all, and that man in the plane was five in all, and that man in the plane was five in all, and ...   ( listing all the five items in the extension of the term  ' the men in the plane ' ).

The descent in such an instance cannot be to a series of propositions, but rather to one single proposition of this sort :

this man in the plane and that man in the plane and that one in the plane and ...   ( listing all the five items in the extension of the term  ' the men in the plane ' ) were five in all.

Here we have one single proposition whose subject term is :  ' this man in the plane and that man in the plane and that man in the plane and that man in the plane and that man in the plane ',  and whose predicate term is  ' five in all '.
Or again consider the proposition

some sort of tooth powder is necessary, if the teeth are to be kept clean.

The subject term  ' sort of tooth powder '  has particular indeterminate designation. Here obviously what is meant is not that some one determinate brand of tooth powder, to the exclusion of all others, is necessary. Instead, what is meant is that some sort of tooth powder is necessary, but it does not make any difference what sort. Thus the descent could not be expressed in a series of propositions stating :

Pepsodent is the tooth powder that is necessary if the teeth are to be kept clean, or else Colgate's is the one, or Dr. Lyons, or Listerine, etc..

The descent is rather of this sort :

Pepsodent or Colgate's or Dr. Lyons or Listerine, etc. (i.e., some one, but without its making any difference which one), is necessary, if the teeth are to be kept clean.

It is now time to investigate (along the lines given by VEATCH, pp.207) the precise bearing of a term's being either a subject or a predicate on that term's (type of) designation.
VEATCH gives two rules that regulate the type of designation of subject and predicate term of a given proposition (one type for the subject term, and [possibly] another type for the predicate term, while these terms still designate the same set of individuals) :

1. With respect to subject terms, the designation is universal in universal propositions, and particular in particular propositions (and singular in singular propositions).

2. With respect to predicate terms , the designation is universal in negative propositions, and particular in affirmative propositions (but singular in singular affirmative propositions [see below]. ( NOTE 43 ).

However, there are affirmative propositions where the predicate term has  universal  rather than particular designation. These are all propositions where subject and predicate are related to each other as  definiendum  to  definiens,  that is, all definitoric propositions.
So it seems that we need a third rule, saying that the designation of the predicate term is universal in (affirmative) propositions asserting a definition of a definiendum.
So it is not in all propositions that the quality of them decides whether the designation of the predicate is universal or particular.

Let me give a few examples that illustrate these rules (where a proposition's being true, or being false, are not intrinsic properties of propositions, that is, truth or falsity have no bearing on the type of proposition just as proposition) :

Universal and affirmative propositions ( = A propositions) :

•   ' every man is fair '  ( = false).
  (with 'man' is, in our expositions not meant only the male part of humanity, but all of humanity, men, women, and children).
  Subject  ' man '  has universal designation, because the expression  ' every '  gives the term natural supposition.
  The predicate  ' fair '  has particular designation, because its maximal extension, consisting of all fair things, is restricted to fair men, where the proposition asserts that all men are fair. 'Restricted' that is, because other things than men, being fair, are not beforehand excluded. If we have a problem with this, we could consider, say, the proposition  ' every man is brown '.  There are clearly other brown things than men.

•   ' every crystal is blue '  ( = false).
  Subject  ' crystal '  has universal designation, because of  ' every '.
  The predicate  ' blue '  has particular designation, because the subject term  ' crystal '  contracts the extension consisting of all blue things  to  all blue crystals, where the proposition asserts that all crystals are blue.

•   ' all crystals are periodic physical bodies '  ( = true).
  Here the subject term  ' crystals '  has universal designation, because of the expression  ' all '.
  The predicate term  ' periodic physical bodies '  must, like in all genuine propositions, designate the same individuals as the subject term does. But in the present case this set of individuals which is designated by the term  ' periodic physical bodies '  is not the result of contraction of some maximal set of individuals :  All periodic physical bodies are crystals (because they are so by definition). So the designation of the predicate term  ' periodic physical bodies '  in the proposition  ' all crystals are periodic physical bodies '  is  not  particular but universal. It covers its whole natural extension.

•   ' all white men are fair '  ( = false).
  Here the subject term is not  ' men '  but  ' white men '.  It has universal designation, because of  ' all '.
  The predicate term  ' fair '  has clearly particular designation.

•   ' no man is fair '  ( = false).
  This is equivalent to  ' every man is not fair '.
  The subject term  ' man '  has universal designation because of  ' every '.
  The predicate  ' fair '  has universal designation, because the natural ( = maximal) extension of the concept  ' fair '  is not restricted by the subject term  ' man ',  by reason of the fact that   ' fair '  is denied by the proposition to be associated with  ' man '.

•   ' no man is living in the sea '  ( = true).
  Here the same holds as for  ' no man is fair '.

•   ' some men are fair '  ( = true).
  The subject term  ' men '  has particular designation, because of the expression  ' some '.
  The predicate term  ' fair '  clearly has particular designation :  We have a contraction here from all fair things  to  some fair men.

•   ' some men are living in the sea '  ( = false).
  The subject term  ' men '  has particular designation, because of  ' some '.
  The predicate term  ' living in the sea '  clearly has particular designation, because  all things living in the sea ( = maximal extension of the concept  ' living in the sea '  [or, equivalently,  ' sea beings ',  or  ' mariene beings ' ] )  is contracted  to  some men living in the sea.

•   ' some men are not fair '  ( = true).
  The subject term  ' men '  has particular designation, because of  ' some '.
  The predicate term  ' fair '  has universal designation, because the subject term cannot contract its natural extension, by reason of the fact that  ' fair '  is not associated with  ' men ' in the proposition.

•   ' some men are not living on land '  (but these men naturally live in the sea or in the air) ( = false).
  The subject term  ' men '  has particular designation, because of  ' some '.
  The predicate term  ' living on land '  has universal designation, because its natural extension is not restricted by the subject term, by reason of the fact that it is not associated with the subject term by the proposition.

And now, what about  negative  propositions?
In such a proposition something is denied of the subject.
If it is denied of all the individuals of the subject term's natural ( = maximal) extension, then we have an E proposition, such as :  ' no man is fair ',  which is equivalent to  ' no men are fair men '.
If it is denied of only a part of the subject term's maximal extension, then we have an O proposition, such as :  ' some men are not fair '.
And because of this denying there is no demand that the predicate and subject term designate the same individuals. Indeed, the proposition says  ' are not '.
According to the rule, just as predicates of affirmatives are undistributed, and thus their designation particular, so are the predicates of negative propositions distributed and thus their designation universal.
In further explanation of this we may note, to begin with, that when a predicate is applied to a subject in a negative proposition, one intends not to combine the predicate with the subject, but rather to separate or divide it from it. Moreover, what is thus separated or divided or excluded from the subject is not necessarily the predicate's mere nature or essence to the exclusion of the items in its natural extension that have that nature, but to exclude  individuals  of its extension. This we can see when we consider the proposition :

no circles are rectilinear,

which is an E proposition (negative and universal), and see that it is equivalent to the proposition :

no circles are rectilinear figures.

And why has the predicate here universal designation? The reason is that in such a negative proposition what is divided or separated from the subject is not a mere portion of the predicate's extension, but the whole of it. Thus it is not just certain determinate rectilinear figures, nor is it merely some rectilinear figure or other, that circles are said not to be. Instead, any and every figure possessed of this nature is divided from those beings designated by the subject term  ' circle '.  Moreover, the proof of this can again be had through resorting to descent, for if the designation be universal, then the descent will be to a series of propositions conjoined by  "and".  Clearly, from the proposition here considered, we can make the descent to the following :

no circle is this rectilinear figure, and none is this one, and none is this one, etc.

And the same principle, just expounded for E propositions, pertains to O propositions, i.e., to particular negatives. That is to say, the designation of the predicate is here also universal, and this, despite the fact that the designation of the subject is particular. For instance consider the proposition :

some substances (in the chemical sense) are not radioactive.

Here what the subject term designates are some determinate items within the extension of  ' substance '  (such an item can be the total individual set of existing atoms of a certain atomic species). So the subject term's designation is particular (and determinate). To explain this designation, first consider the effect of the expression  ' some '.  This expression makes the designation of the subject term  ' substances '  particular. But as such, that is, in considering only the  ' some substances '  part of the proposition, it is still indeterminate, like it would be in a proposition like  ' some substances are needed to make a house '.  So the items in the extension of  ' some substances '  could be any substances. And from precisely such an indeterminate set of items the proposition divides or excludes in toto all those things that are said to be radioactive. Now the designation of the subject term  ' substances '  has become determinate. And because, as has been said, all radioactive objects are excluded by the proposition, the designation of the predicate term  ' radioactive '  is universal (and distributive). All the items or individuals designated by the subject term (the total of all non-radioactive substances) are clearly not the same items or individuals designated by the predicate term (the total of all radioactive substances), but this is no problem, because the proposition separates, instead of combines, subject and predicate.
Again we can prove this by resorting to descent :  Descending to the particulars we get :

some substances are not this radioactive object, and some are not this one, and some are not this one, etc.

So the predicate term has indeed universal (and distributive) designation.

This completes our account (as we have found it in VEATCH and, after some amendments, approved of )  of the relevance to designation of a term's position as subject or as predicate in a proposition.
But before we leave this topic, we will say something about designation of terms in  singular propositions.
In the singular proposition

Franklin Roosevelt was a distant cousin of Theodore Roosevelt

the designation of the predicate term  ' a distant cousin of Theodore Roosevelt '  is, according to VEACH, p.210-211) "clearly common". Moreover, just as in ordinary universal or particular  affirmative  propositions, the designation of the predicate term is particular (as a species of common)  and  indeterminate.
On the other hand, were one to say,

Franklin Roosevelt was the next president after Hoover,

or,

was the thirty-second president of the United States,

or,

was the only son of Sarah Delano Roosevelt

-- in all of these cases the designation of the predicate would not be common (and thus also not particular) but singular.

Let me comment on all this.
In the (first mentioned) proposition  ' Franklin Roosevelt was a distant cousin of Theodore Roosevelt '  the designation of the predicate term is, according to me, not common but singular (while its maximal extension consists of all distant cousins of Theodore Roosevelt) :
The  signification  of the concept  ' distant cousin of Theodore Roosevelt '  is the nature  distant cousiness of Theodore Roosevelt,  while the maximal or natural extension of this concept consists of all the individual distant cousins of Theodore Roosevelt. But in the proposition  ' Franklin Roosevelt was a distant cousin of Theodore Roosevelt '  this extension is, because of the singularity of the subject term, contracted to one individual only. So the designation of the predicate term is singular, not common. And because the proposition asserts Franklin Roosevelt to be  a  distant cousin of Theodore Rossevelt, we do not know from this proposition how distant a cousin of Theodore Roosevelt he is. So the singular designation is in this respect  indeterminate.
On the other hand, the predicate terms of the three other propositions have, while also singular, determinate designation.

In conclusion of our exposition of the theory of designation we'd like to quote VEATCH, p.211 :

Needless to say, this treatment of the various kinds of designation is perforce sketchy and incomplete. Yet it is perhaps sufficient to show how from the point of view of an intentional logic a proposition is not to be regarded as a mere comparing or relating of two concepts either in respect to their comprehension or in respect to their extension. On the contrary, by recognizing that concepts acquire the property of designation when they enter into propositions, it becomes understandable how a subject and predicate, even though they have different meanings or significations, may nevertheless be used in a proposition so as to designate the same existents.

Unless it is singular, terms in a proposition are (implicitly or explicitly) quantified by expressions like  ' some ',  ' a ',  ' all ',  ' every ',  etc. All these expressions can be reduced to two types :  universal and particular quantification. In mathematical Logic they are symbolized respectively by and .
Thus when  ' f (x) '  is to mean  ' x  is  blue ',  we can quantify this proposition, turning it
either  into  a  universal  proposition :

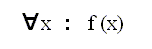
which means :

for every  x  applies :  x  is  blue,

and that is nothing else than

all  x  is  blue,

or also :

every  x  is  blue,

or  (quantification can turn the proposition  ' x  is  blue ' )  into  a  particular  proposition :

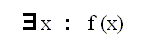
which means :

there exists at least one  x,  such that  x  is  blue,

or, equivalently :

some  x  is (are)  blue.

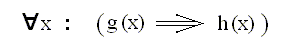
If  ' g '  means  ' (to be a) man '  (or, (to be) human),  and  ' h '  means  ' (to be) mortal ',  then the proposition reads :

for all  x  applies :  if  x  is  a  man,  then  x  is  mortal,

or, equivalently :

all men are mortal.

And if we quantify this proposition differently, we get :

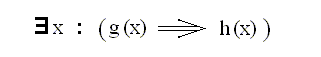
which means :

there exists an ( = at least one)  x,  such, that  if that  x  is  a  man,  then  x  is  mortal,

or, equivalently,

some men are mortal.

This proposition is, of course false, because it lets open the possibility that some other men are not mortal.

Next example :

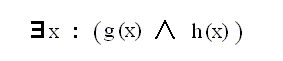
If  ' g '  means  ' (to be a) man '  (or, (to be) human),  and  ' h '  means  ' (to be) wise ',  then this proposition reads :

there is an ( = at least one)  x,  such that  x  is  a man  and  x  is  wise,

or, equivalently :

some men are wise.

So if the variables of a propositional function are given ( = supplied with) values or interpretations, and when the interpretation is such as not resulting in a singular proposition, then such a 'rough' proposition, such as  ' men are wise ',  will be made into a mature propostition (such as  ' some men are wise ' )  by quantifying its terms as is shown above and done so by the mathematical logicians.
Why precisely does (proper) quantification result in a fully-fledged proposition? That is, how do we explain this transformation? Such an explanation is to be found, as VEATCH, p.233, suggests, in the so-called  designatory  function which all concepts must assume as soon as they enter into propositions.
As we now know, in itself, any concept (that is, any concept taken as such) has significance, i.e., has a basic meaning or intension. But only in a proposition does it come to  designate  anything as existing. That is to say, a concept means or signifies a certain nature or essence, and in virtue of this basic meaning we can apply the concept to individuals. Implicitly this is already done by the concept itself, and so constitutes its natural ( = maximal) extension or natural supposition by being just a relation of identity between this meaning and each possible or actual individual in which such a nature or essence exists.
However, no concept just as such ever indicates whether any, or all, or some one, or this particular one, of these individuals exists. Rather it is only in the proposition that this designation of existents takes place. Indeed, as we saw, the very relation of identity between the subject and predicate terms of a proposition is to be understood with reference to the common or identical  designatum  or  designata  of these terms. As concepts they have different meanings, but as subject and predicate terms in a proposition they  designate  the same existent or existents.
Accordingly, when one considers what the full import is of the procedures of substituting values for variables or of quantifying variables in a propositional function, they would seem to involve nothing more nor less than this very designation of existents, which, we know, is altogether requisite if concepts are to function as parts or terms of a proposition. After all, if a concept is to designate items in its extension as existing (in some way or another), it must be determined whether in a given instance the concept is being so used as to designate all such items or some of them or this particular one, or whether it is designating them collectively or distributively, etc. And what is this, if not that very operation of quantification by which the modern logicians say they turn mere propositional functions into fully-fledged propositions?
Accepting this account of quantification in terms of designation, we are thereby provided with an explanation as to what quantification, considered with respect to its intention, really is, and why it is so indispensable if mere propositional functions are to become propositions.
From this cursory description of the two types of quantification, we may note that it diverges in three rather important respects from the traditional description of universal and particular designation, as outlined in the foregoing discussions. ( VEATCH, pp.234 ).
In the first place, the modern logician seems to feel that concepts such as  ' men ',  ' trees ',  ' philosophers ',  ' automobiles ',  ' crystals ',  etc., when they appear as subject terms of propositions, must be subjected to further analysis. The analysis apparently consists in the explicit separation of the individual from its  what -- e.g.,  ' x  is  a  man ',  or  ' x  is  a  tree ',  or  ' x  is  a  philosopher ',  etc.
In the second place, and as a direct consequence of this, any universal or particular proposition of the traditional categorical ( = without conditions) type turns out to be not simple at all, but compound. Thus a supposedly simple, categorical proposition like  ' all men are mortal '  turns out to be a hypothetical proposition. And a proposition like  ' some men are wise '  is held to be a conjunction.
In other words, the whole traditional scheme of universal and particular categorical propositions is completely disrupted, and what appear to be simple subject-predicate propositions turn out not to be so at all.
Finally, this turning of universal propositions into hypotheticals and particulars into conjunctions has the further effect of making the particulars into existential propositions and the universals into nonexistentials. That is to say, on the new theory (of the mathematical logicians), only particular propositions intend existence, or better, consider the objects of their intention as being or existing.
Obviously, in the light of these divergances, the question arises as to whether the theory of quantification, which is, as we have seen, in so many ways quite comparable to the theory of designation in intentional Logic, but which nevertheless in these other ways is so strikingly different from it, is, after all, really an improvement on the theory of designation  ( VEATCH, p.234-235 ).

To assess all this is in fact to investigate whether intentional Logic, with its theory of designation, is able to deal with the problem of the null class, to which we shall turn in the next document.

e-mail : 
( Please write in  ' Subject '  entry :  ' METAPHYSICS ',  in order for me to be able to distinguish your mail from spam )

Back to Homepage

Back to Contents

Back to Aristotelian metaphysics Part I

Back to Aristotelian metaphysics Part II

Back to Aristotelian metaphysics Part III

Back to Aristotelian metaphysics Part IIIa

Back to Aristotelian metaphysics Part IV

Back to Aristotelian metaphysics Part V

Back to Logic Part I

Back to Logic Part II

Back to Logic Part III