e-mail :
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam ) Intentional Logic consists of three major divisions, viz., the Concept, the Proposition, and the Argument.
A concept lets us know the what of a thing, of a feature, or of an event.
A proposition explicitly states this what as existing. Therefore, a proposition can be either true or false.
An argument is supplying evidence for the truth of some proposition.
The argument adds a reason for some assertion. So this reason is a crucial part of the argument.
What, in extramental reality, is such a reason supposed to intend?
What does this reason intend in support of the inherence of a feature in that what the subject term (of the conclusion) designates? Most naturally this would be the cause of that inherence. The argument discloses, by means of its reason, the cause of the fact that the significatum of P (predicate term) inheres (intrinsically or extrinsically) in the designatum of S (subject term).
So now we not only know the fact that the significatum of P inheres in the designatum of S, but also why it does so.
But an argument is not exclusively a device to show the cause of some asserted state of affairs. It is a device of making evident that state of affairs. And that means that it could do so also by pointing to the effect (instead of the cause) of that what should be made evident. The presence of some specific effect points to that state of affairs if the latter is the proper (sustaining) cause of that effect. Of course we then know, it is true, that that state of affairs must be present, but still we do not know why it is present. But the function of the argument is solely to make evident the presence of that state of affairs (concluding as it would do : 'therefore, such a state of affairs must exist').
So generally we can say that a (deductive) argument intends one or another causal pattern or structure. Said better, a (deductive) argument intends, first of all the general ontological pattern of a causal structure. That is, the general structure of argument (which is a logical structure) intends the general ontological structure of a causal pattern (cause of state of affairs [which state is to be rendered evident by the argument] and this state of affairs, or this state of affairs and that what is in turn caused by it). The specifics of the argument then render the intention complete.
How does such a general ontological causal pattern look like?
Initially, we are inclined to see this pattern as consisting of two entities, viz., the cause and its effect, and, in such a way that we say that there is first the cause, and then, following in time upon it, its effect.
In terms of dynamical systems (which is a good image of [things going on in] extramental reality) we think of any two consecutive states of a given dynamical system as follows : If one state is considered an effect, then its previous state is its cause. This sounds pretty good, but is false.
The coming into being of state Zn+1 of a given dynamical system is simultaneous with the disappearance of the previous state Zn. How, then, can state Zn cause state Zn+1 by disappearing?
State Zn+1 for coming into existence needs the action of state Zn : The existence of the effect is the action of its cause. Only in this way can a cause bring about its effect. The cause, precisely and only insofar as it is the cause of its effect (and thus not broadening this idea of cause to cover the whole entity that carries and transports this cause), is in that entity in which this effect inheres. Further below we will work out this topic further.
A cause can be intrinsic, like the material and formal causes. As such it is a metaphysical component of a thing.
A cause can also be extrinsic or physical, such as the efficient cause. And such a cause is also in the thing (in which it produces its effect), but is nevertheless extrinsic to it.
While the matter and the form are parts of the thing's essence, and so come from within, the efficient cause comes from without : A causal chain, or carrier and transporter of that what will become a cause, starting somewhere outside the thing (the patient), enters this thing with its last link which is the efficient cause proper. That is, the (efficient) cause of some effect is only then this efficient cause when it is in the thing which is going to carry the effect.
It is such causal patterns, involving intrinsic or extrinsic causes and their proper effects, that are intended by arguments.
The argument intends the existence of an entity-as-being-derived-from-something-else. This is the simultaneous causal structure or pattern. The argument discloses the being of an entity in and through cause and effect.
In an argument the why of things, or the reason of their being or existence, or the evidence of their being (present in or on something) comes to be known by the relation of triple identity S is M is P, where M signifies the cause or effect and so making evident that S is P. Indeed, it is because the cause is in that which carries the effect, that the causal structure can be intended by the relation of triple identity between S, M, and P. Of course this demands a correct designation of the terms in an argument. We shall develop this theme little by little in what follows.
The material cause, as material cause, cannot play a role in an argument because it is not specific. If we use it nonetheless, namely when calling upon a specific substrate, we in fact use a formal cause.
A specific proprium (that is an attribute that occurs in all individuals of a species and only in these individuals) can be demonstrated through -- ultimately -- the definition of the subject (of the conclusion). From this definition, namely, we can derive the middle term of the syllogism, as is shown in Aristotelian Metaphysics Part V Via Diffinitionis, b. And this means that the evidence consists in pointing to the formal cause, which is the essence of the subject, that is, the essential formal content that is signified by the subject term of the conclusion. For material things such a proprium is initially found out to be a proprium by induction, which is nothing more than the detection that a certain formal content goes together with the individuals of a given species in all observed cases.
By induction, that is, by generalizing facts of experience, one finds rules governing certain natural processes or dynamical systems. Initially these rules are just crude models of the real process that one wants to understand. They must subsequently be perfected by further investigation. The rules then become laws, that is, natural laws.
If we now apply these laws we perform deduction : We predict a next state of some (real) dynamical system governed by such a law ( The perfection of the model already goes by repeatedly applying the assumed rules for relevant cases and seeing whether the predictions, resulting from such applications, come true or not).
The application of the law or set of laws (generally expressed in the form of an equation or set of equations) representing the model, (the application) in the sense of the prediction of te next system state is the course from the general to the special, which can be done by a syllogism.
It is the course from
general relation between (any) two consecutive system states ( = dynamical law)
to
special relation between a given system state and the next state.
The general relation between consecutive states can be complicated and non-linear, and is, as dynamical law, found by induction.
Let us now see how a s y l l o g i s m demonstrates a given system state, that is, shows why this state is what it is :
The syllogism here is clearly one that goes from the general to the special.
' (is) related to the previous state as y : x '
is (or signifies) a specific proprium of : state of dynamical system DELTA (and is of course the essence of dynamical system DELTA ). And from this (specific proprium) we can conclude to ' related to the previous state as y : x ' being a generic proprium of state B (that is, of state B of every dynamical system DELTA ). It is generic because also all other states of dynamical system DELTA possess this attribute.
The syllogism demonstrates an essential attribute of state B of dynamical system DELTA, by disclosing B's formal cause. An efficient cause, here, will only be at work in the case of a perturbation of the system by agents coming from without.
Having found a syllogism that reveals why state B is what it is, we must now find a syllogism that reveals that state B is, i.e., that reveals why we now actually have before us state B (and not, say, state A, C, D, etc.) of dynamical system DELTA.
Here the expression "one state earlier" means : a point in time that is one tick of the dynamical clock earlier (where the system is considered to be a discrete [as contrasted to continuous] dynamical system). Now the syllogism.
Here, the evidence or reason of the presence of state B is the existence, one state earlier, of state A.
Another example of a syllogistic argument going from general to special is :
A man is mortal because he is an organism. Here the conclusion is made evident by revealing the substantial form of the subject, that is, by pointing to it. This form is here [partially] expressed by being an organism. So the conclusion is made evident through the formal cause of its subject. The syllogism demonstrates an essential attribute, although it is not an attribute that is specific.
Let us now try to demonstrate why a given individual volume of water gets warmer. So what we're taking about here is that something is happening to a here-and-now volume of water : it (is observed that it) gets warmer, and we want to know the cause of this event.
Generally, water will get warmer by heating it, that is, by supplying it with heat energy, but it will only get warmer, if so supplied, as long as it is still below its boiling point. So addition of heat energy is the cause of the warming up (increase in temperature) of the water.
Let us now try to capture the described individual event in a syllogism :
Here, however, we have not demonstrated why a given volume of water has become warmer. For this the answer should be that it was heated, that is, that heat energy was actually supplied to it.
The following argument shows that it is nevertheless possible to capture the above described individual event (of a given volume of water getting warmer) in a syllogism, that is to say, it is also possible for a syllogism to demonstrate an accidental attribute. Thus it will be shown that the syllogism can not only intend causal structures involving a formal cause, but also those involving an efficient (that is, extrinsic) cause. But because the attribute is accidental, it cannot pertain to the subject taken generally (it cannot necessarily pertain to all individuals of the species). Such an attribute attaches to some one individual here-and-now subject or another ( When we say "subject" here, we mean that what is designated by the subject term. Such an individual here-and-now subject is, for instance, ' this [particular volume of] water [here] ' ) :
So the argument makes evident why this (particular volume of) water here gets warmer : it is being heated.
A comparable syllogism, that is, a syllogism demonstrating the presence of an accidental attribute by revealing the efficient cause, is given by VEATCH, p.302 :
So Smith is suffering from pneumonia because he was exposed to cold.
And if, when we do not assume this (say, by having found out that some type of people cannot catch pneumonia in this way), we change the minor premise into ' Smith is such a " whoever " ', then we have again a demonstration through the formal cause. But now the conclusion would be : Smith will come down with pneumonia when he is exposed to cold. And again (as we had it in earlier cases) the syllogism has demonstrated an essential attribute, now of Smith, although this attribute is not typical for Smith, that is, it is not an individual proprium.
We have shown syllogisms that reveal the cause of some state of affairs. In our examples these states of affairs were
As for case (1), a new state of a dynamical system is the necessary result of the interaction of the system elements. So the next system state necessarily follows upon its previous state. Of this previous state we can say that it is as such not the cause of the next state, because the latter is consequent in time upon the former. We can, however, say that the previous state carried the cause. And insofar as it carries the cause the previous state is still in the next state. What is, however, important in the present discussion is the fact that necessity is involved when one state follows upon its previous state.
But what about the water volume that is before us now and which is getting warmer? The cause was, as revealed by the syllogism, that it was being heated. With respect to the water volume -- as a physical system or configuration -- this heating is accidental : having some volume of water does not necessarily entail that it will be heated. On the contrary, the water just happened to be heated by some external energy source like a bunsen-burner.
But in fact we can say that the water has changed its state : it has gotten warmer. More precisely, we must include the burning bunsen-burner, or at least the heat that it is emitting, into the dynamical system at hand. If we do so, the water necessarily gets warmer.
The same applies to Smith, who apparently happened to be exposed to cold. If we now include Smith's environment into the system, then he was necessarily exposed to cold and as a consequence came down with pneumonia.
So in the last two cases, we have, as in the first case, a necessary following up of states of a certain dynamical system, implying as it seems, that the cause had preceded in time its effect (above we already hinted to this).
We know, however, that this cannot be so, because if the cause precedes its effect the latter cannot come from the cause. So the 'cause' as it is supposed to be signified by the middle term in the arguments that demonstrate the presence of a state of a given dynamical system, is in fact not a cause, but is something that can figure as a reason or evidence for the existence (or reason to assert this existence) of that particular state.
The real causality is not between a state and its previous state, but is buried deep within the dynamical system : It is at work there where the system elements interact, and perhaps it lies even deeper. It certainly involves energy transfers rendering a certain material configuration more stable than the initial one. Here we probably are already at the quantum mechanical level, where the notions of genuine being and of definiteness seem to fade away.
So indeed it is best to stick to the rationalistic approach, that is, to the metaphysical approach, in establishing the nature of causality, because it doesn't present itself empirically. This rationalistic approach reasons that the effect is the action of the cause, so that the cause is in that which carries the effect, or, maybe better : that the effect is its cause. And this not only with respect to the material and formal cause, but also to the efficient cause. The efficient cause is the end of a chain of which the last link is (in) the effect, or, perhaps better : in that which carries the effect.
Arguments demonstrate that S is P by calling upon evidence. This evidence can be a cause, an effect, or just a compelling reason. While arguments often are about the attribution of something (essential or accidental) to a genuine substance (in the metaphysical sense) or totality-generating dynamical system, they can also be about some dynamical system that does not generate such a totality or substance or is not itself such a substance. In addition, arguments can also be about the attribution of something to aggregates (of substances). These aggregates are then considered as if they were substances.
The next syllogism is about the demonstration of an attribute of such an aggregate from the 'intrinsic form' or 'essence' of the aggregate, that is, a demonstration of the attribute from its cause, which belongs to, or is itself derivable from, the subject's essence :
Where absorbent is a genuine property of towels.
For non-essential predicates we can, as has been said, resort to a cause as evidence, but also to an effect, namely when the cause of the attribution, as this attribution is expressed in the conclusion, is not known. Such cases can be catched in an argument which here is a hypothetical syllogism. For instance :
So, assuming that we do not know what the barometer actually measures, we can say that it will rain because the barometer is going down. In fact the going down of the barometer is an effect or sign (and thus not a cause) of the decrease in atmospheric pressure, which itself is among the causes or forerunners of rain.
Accordingly, demonstration of generic or specific properties, or of accidental determinations, can go about either by pointing to their cause or to their effect or to a sign of their cause or to a sign of their effect, etc.
But what about definitional propositions, that is, propositions predicating a genus, a differentia, or a definition of the subject? In such cases no cause is involved, because here the subject term signifies some essence, while the predicate term signifies what that essence is. But an essence is what it is solely in virtue of itself. So no middle term can be called for. Nothing can fit in between what something is and what something is.
So in the case of definitional predicates, there are no causes, and thus also no effects. Nevertheless, for evidencing we can use a quasi effect : A quasi effect is either
A cause, in cases where there is a cause, can be a mediating entity between that in extramental reality upon which the effect is exerted and the effect itself : In the typical case of an accident coming to be in a substance, the cause has its effect upon the substance, just as the effect itself is the actualization of the accident in the substance. When the 'pre-cause' has entered the substance, it is, as coming from without the substance, called the cause, and, as being in the substance, called the effect. The cause can then be intended by the middle term of a syllogism.
But we must be aware that an argument, as being a logical intention, can be much more flexible than the real (causal) pattern it intends : while the real order is always from cause to effect, the logical order in an argument can be the other way around, or even just calls for an effect or a sign. So we must be keen not to confuse the logical with the real. And now it is clear that a logical relation of (triple) identity, S is M is P, can intend the real association of cause and effect or (can intend) things in their being pointed to by, and thus associated with, (natural) instrumental signs. Here, because S is M and P is M, we can legitimately conclude that S is P. In this way the argument S is M is P intends some real pattern, and makes evident that P's significatum indeed in reality inheres in S's designatum or designata.
Like it is in propositions that the purely intellectual distinguishing and re-identifying of the subject term and the predicate term is founded upon, though it is by no means to be confused with, some sort of real distinction and union in extramental reality, resulting in an isomorphy (but not an identity, and not even necessarily a similarity), so it is with the argument and its relation of triple identity. It is founded on some real pattern involving real dependencies, also resulting in isomorphy
( NOTE 46 ).
For propositions the predicable relationship of accidental predicate term to subject term is founded on the real (transcendental) relation of accident to substance. Yet that does not mean that in a proposition an accident is ever as such predicated of a substance, for no substance ever is formally its accident, and likewise with the other predicable relationships. The correspondence is no more than an isomorphy.
The predicable relationships of genus to subject and of differentia to subject (as in ' man is an animal ', respectively ' man is rational ' ) are founded on the real relation and distinction in any finite essence between matter (genus) and form (differentia). Or the relation of species to subject (as in ' Socrates is a human being ' ) is founded on the real distinction and relation of essence to supposit.
And so it is with an argument too : It is founded on some real pattern of dependency. And also here the logical, which here is a relation of triple identity between terms (S is M is P), should not be confused with the real that is intended.
The cause, as effect, is in the patient (that is, in that, upon which the cause exerts its influence), so the cause precisely as influence is in the patient. In this way we can say that the cause, the influence ( = the acting upon) the effect and the patient are united. And indeed, as such the relation of triple identity is perfectly suited to intend that real unity.
Such a genuine, that is, most proximate (to the patient), and thus inhering (in the patient), cause is always connected with more remote causes that we find along the chain leading to the patient. And it is often mere these that are explicitly intended by the middle term of a syllogism, if it intends a cause (of the entity to be proved) at all, and not just the effect of the entity to be proved (the effect then figuring in the argument as reason or evidence of that entity). But, in addition to explicitly referring to such a remote (and therefore external with no qualification) cause, the middle term, I think, implicitly refers to the very proximate cause, and it does so by intending the remote cause as if it were the proximate cause.
The whole causal situation and its being intended, can be diagrammatically expressed. Let us do so.
That in reality what the term S designates, we will call SR .
That in reality what the term M signifies, we will call MR .
That in reality what the term P signifies, we will call PR .
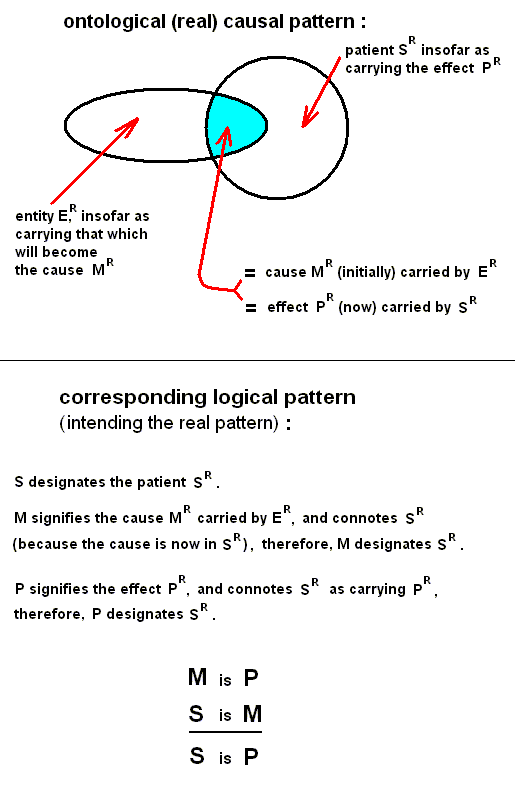
So S, M, and P, have the same designatum, namely SR . Therefore, the terms S, M, and P, can be identified : S = M = P, and so we have our syllogistic demonstration.
As an example we can say :
The heat energy carried by infrared radiation, or by a (hot) substance, is entering a given volume of water. As soon as this energy is in the water, that is, as soon as the water now carries this supplied energy, it is the cause of the water getting warmer. And to get warmer (before the boiling point is reached) is in fact the same as to possess more and more energy, that is, kinetic energy of the water molecules.
So here we clearly see that the very proximal cause is the effect.
All this, about causal structures and how precisely they are intended by syllogisms, is no more than a suggestion. Moreover, it deviates in some important respects from the corresponding account given by VEATCH.
Induction.
Induction, or inductional inference, is a generalization of some state of affairs as it is found in a number of individual instances (observations, experiments), over all actual and possible instances.
It is part of the general method of natural science, and indeed the largest and most important part of that general method.
Induction is based on, and legitimized by, an important presupposition of all natural science (and beyond), which has been called the " Species-Individuum Structure " as obtaining in all natural objects and events, and even in mathematical formalism. According to it, it is presupposed (and it is a necessary presupposition, because its denial would render all induction, and consequently the basic method in science, impossible) that any formal content, whether it is an essence of a substance or an essence of an accident, or whatever formal content, can in principle be repeated over several instances (and is in fact often so repeated). Such a formal content can then be in this supposit here and now, but also in that supposit there and now, or in that supposit here and then, etc. This supposit is the individuum-part of the Species-Individuum Structure, while the species-part symbolizes the formal content which can be repeated.
In this way properties (propria) of something (which is a substance, or interpreted as a substance) are, first of all, actually found in some instances and are then generalized over all relevant possible or actual instances according to the mentioned presupposition.
So, to take an example, the property of iron to be susceptible to being magnetized is first found for a number of individual pieces of iron, while no exception is found. Then one will generalize these individual findings over all actual and possible pieces of iron whatsoever, that is, that all iron behaves like this, and, not only so in the present, but also (it had behaved so) in the past, and (will behave so) in the future. Later, when one will understand completely the nature of iron, that is, its essence, one will be able to deduce this property of magnetization from this essence. One has then demonstrated the property, a property which initially was known only by induction.
To repeat, in experience we observed that iron (that is, that what we use to call iron, on the basis of some other properties) and magnetizability always (that is, in all observed instances) went together. We then generalize this, and claim that the two always go together in all possible and actual instances, whether observed or not, and whether these lie in the present, past or future.
The greater the number of actually observed instances, the more certain is the inductive conclusion. And when we finally come to know the essence of iron more or less completely, we are coming to be in a position to deductively verify the induction, by deriving it directly from the essence of iron.
The argument that legitimizes the induction of the property in question of iron can be cast in the following syllogism :
When we now experimentally find the property of magnetizability for a number of pieces of iron, and have not found exceptions, then we apply generalization, that is, induction, where the instances are all pieces of iron. And this induction is the conclusion of the above argument. This argument shows induction to be legitimate on the basis of the presupposed Species-Individuum Structure of things.
Induction and definition.
The what of some essence as asserted in a definitoric proposition, say, ' man is a rational animal ', cannot be proved by disclosing a cause. Is, then, a proposition, asserting a (non-arbitrary) definiens of a definiendum, the result of induction?
Well, in retrospect, we can say that the content rational animal was found in those (investigated or experienced) instances which we call human beings, and was then generalized to include all possible and actual instances. This is clearly induction. The result of the induction is then that every human being is a rational animal, laid down in the proposition ' man is a rational animal '. However, now knowing -- by induction -- that man is a rational animal, we still do not know why man is a rational animal. If we re-interpret ' man is a rational animal ' as a definition of the term ' man ', then it is perforce self-evident. But if we do not so re-interpret it, then we can still ask why man is a rational animal. And the answer must be found in biological results : Man has, in organic evolution, inherited animal nature, so he is some sort of animal. And the evolutionary development of his animal brain has been such as to endow him with rationality, so he is a rational animal.
All this is established on the basis of individual findings in a number of particular instances, generalized over all possible and actual instances. Also we must find out why the evolution of the sistergroup of the Apes (to which latter now belong Chimpansee, Gibbon, and Gorilla) went that way and ended up with humans, that is, rational animals. If we know all this, then we know why the organisms which we call human beings are rational animals.
Again, as a definition -- man is a rational animal -- we cannot find the 'why' in terms of something extrinsic to rational animality : Man is then a rational animal wholly in virtue of himself.
Induction and models.
The use of models in science is but a sophisticated version of induction as described above. A model is a supposed (that is, supposed to be present in extramental reality) structure or regular process, inspired by, and geared to, observed facts which one wants to explain. The testing of the model is in fact an application of induction : to see whether the model holds in all relevant instances. If it does so for a sufficient number of instances, and when no exceptions are found, the model is accepted (if there are several models doing the job, one chooses the simplest of them). And such a model, no matter how complex it may be, is, I venture to say, in fact a proposition, and as such a logical intention.
As long as the model is still rough, it cannot be such a proposition, but when it is refined it can be supposed to intend something in extramental reality. And if it intends that something in reality that it was designed to explain, then the model, as proposition, is true.
Such models are often cast in mathematical forms. And as such, of course, they are not intentional. Only when they are physically interpreted, they can be intentions, that is, intentions of patterns in extramental reality.
A good general example of a model is an equation, or set of equations (most often differential equations), that is said to be a model of some real dynamical system, like the weather system for instance. When such a model is supplied with an actual existing (measured) initial condition or state, and when, in addition, the mathematical symbols are physically interpreted, the model can make predictions (as one does in weather forecasts) as to subsequent states of the real dynamical system (In fact what one does is mathematically solve the equation, resulting in a whole set of possible trajectories of the system, and when one now introduces a measured intial state or condition, one such trajectory is then automatically singled out, giving the predicted sequence of system states). Such a prediction (of a single state) then boils down to being a subject-predicate proposition about some real state of affairs, and later observations can verify (or falsify) such a prediction ( Theoretically, one now can also say that the new state of the system when it has appeared is explained by the model). The model will then be refined if necessary. If one speaks of an isomorphy between the mathematical form of the model and the real situation, the mathematical model is not therefore intentional (because a mathematical model isn't intentional at all). But when the mathematical symbols are interpreted, and the model supplied with an actually measured initial condition or state, then the model is intentional ( This -- preliminary -- view of mine deviates somewhat from that of VEATCH in this respect).
Logical intentions, as intentions, and their bearing on objective knowledge.
If there is to be objective knowledge of any given thing (s.l.), we must know that thing, and not just a(n) (mental) image of it. This means that if there is to be objective knowledge, there should not be any mediating entity between the knowing power and the thing known. And this in turn means that there must be a formal identity between the thing known and the intending logical entity.
How does a logical sign, such as a concept, a proposition, or an argument, attain this formal identity with the real objects or patterns intended? Or, in other words, what precisely is such an identity, and how, precisely, does it as such, and only as such, guarantee objective knowledge?
REMARK :
Of course we have already discussed this topic, because it is crucial to an acceptance of an intentional Logic. However, we do not pretend to have -- in those earlier discussions -- settled the issue once and for all. And because now we know so much more about what an intentional Logic must look like, we can supplement our earlier discussions of this important topic.
The formal identity between logical entity and object to be known, which (identity) will be shown to be necessary for knowledge to be objective, must in some way be equivalent to the ' being about ' of the logical entity. The what of a logical entity solely consists in its being about something else, and this is accomplished by actually being that something else. The logical entity then intends an object. And such a logical entity is first of all a concept.
REMARK :
In what follows we first of all think of empirical concepts, in contrast to theoretical or hypothetical concepts such as 'phlogiston', 'natural selection', 'energy', 'causality', etc.
And because of this formal identity, the specific formal content, i.e., the content commonly possessed by logical entity and thing intended by it, can be predicated of individuals, that is, the individuals of the concept' extension.
If we name the content of a given concept " Aconcept " and the corresponding content in the individuals of the concept's extension " A ", where Aconcept = A, then we have for every individual (thing) S (of the concept's extension) :
individual (thing) S carrying Aconcept = individual (thing) S carrying A.
So if, for example, Aconcept being the formal content ' humanity ', then we have the identity of
Socrates-carrying-the-content-of-the-concept-'humanity'
and
Socrates-carrying-the-form-HUMANITY,
implicitly expressed in ' Socrates is human '.
And this guarantees an immediate contact between the knowing power and the object to be known, and thus guarantees objective knowledge.
In ' Socrates is human ' the term ' Socrates ' stands for Socrates-carrying-the-form-HUNANITY, while the term ' human ' stands for Socrates-carrying-the-content-of-the-concept-'humanity'. These designata are identical.
The same goes for the concept ' tanned ' : Here we have the identity of
Socrates-carrying-the-content-of-the-concept-'tannedness'
and
Socrates-carrying-the-form-TANNEDNESS,
implicitly expressed in ' Socrates is tanned '.
Also here the immediate contact between the knowing power and the object to be known is guaranteed, and thus objective knowledge is guaranteed.
In ' Socrates is tanned ' the term ' Socrates ' stands for Socrates-carrying-the-form-TANNEDNESS, while the term ' tanned ' stands for Socrates-carrying-the-content-of-the-concept-'tannedness'. And also here the designata are identical.
When we now are actually going to use the concepts, the identity reappears in the e x p l i c i t (that is, now actually spoken or written) predications : ' Socrates is human ' and ' Socrates is tanned ' (which are subject-predicate propositions). That is to say, if we want this knowledge to be objective when using the concepts, we must engage in subject-predicate propositions, because only then we let reappear the identity (already present in the concepts and thus in the mentioned implicit predications that constitute the concepts).
The logical entity Socrates is human, which is a logical relation between terms, intends the real relation as it is between a supposit and an essence.
The logical entity Socrates is tanned, which is also a logical relation between terms, intends the real relation of the inherence of an accidental form in a substance.
What about the proposition
tannedness inheres in Socrates ?
This proposition is not a subject-predicate proposition. It does not (explicitly) express i d e n t i t y between
Socrates-carrying-the-content-of-the-concept-'tannedness'
and
Socrates-carrying-the-form-TANNEDNESS,
but expresses i n h e r e n c e. It does not, however, do this latter by having the term ' tannedness ' inhering in the term ' Socrates ', because terms cannot inhere in other terms. And this means that the proposition ' tannedness inheres in Socrates ' does not really intend anything in extramental reality, although it does point to something in that reality. But it points to it not as a formal sign (a sign that really intends) but as an instrumental sign. It instrumentally points to the tanned Socrates. That is to say, the mental counterpart of the (conventional) word string ' tannedness inheres in Socrates ' is some sort of image that is caused by, or similar to, the real tanned Socrates. So this mental counterpart is a real relation pointing to another real relation. In this way tannedness inheres in Socrates is a real relation, a mental picture. Therefore it does not intend anything. And only when this mental image is isomorphic with the tanned Socrates it points to this state of affairs, but only instrumentally so, because the other condition for a sign to be formal (that is, intentional) is still wanting, namely the proposition to be a subject-predicate proposition (where the above mentioned identity naturally reappears). There is no immediate contact between the (mental counterpart of the verbally enunciated) proposition ' tannedness inheres in Socrates ' and the tanned Socrates. Consequently, it does not guarantee objective knowledge. We know the mental image, but not the fact itself.
And, returning to arguments (as logical intentions), it is now clear that if an argument is to convey objective knowledge, its constituent propositions must be subject-predicate propositions, because only such propositions involve identity. And then we automatically have to do with a syllogism. All other types of arguments only instrumentally point to a causal structure, and this only when there happens to be an isomorphic relationship between the argument and the causal structure (to which the argument instrumentally points). And we can expect such an isomorphy to be present when the subalterns of the argument turn out to be correct predictions. That is, when we deduce special instances of the general argument. These predictions are correct when they turn out to comply with observations.
We now have given the conditions for knowledge to be objective knowledge.
But is all knowledge (ultimately) objective? That is, are the above established conditions really present?
Well, although we can, from a realistic point of view (that is, from the point of view of a realistic metaphysics) say that the proposition ' some aspects of knowledge are subjective (with respect to the human knowing power) ' itself pretends to be a piece of objective knowledge (implying that certainly not all knowledge is subjective), it does not necessarily mean that then all knowledge is necessarily objective. Statements about knowledge can (be conceded to) be objective, but that does not exclude that some, or maybe all, knowledge about things could be subjective (subjective, that is to say, with respect to the human cognitive power, and (subjective) in the sense of all its signs being not formal, but instrumental). Indeed, in natural science models are set up to explain things in reality. Some of them are discarded later on, while others are more and more improved, until they indeed make the right predictions, that is, until they hold against observational scrutinity.
In our exposition we have investigated things under the supposition that ultimately all knowledge is objective. But the above considerations have shown that it is certainly worth the trouble also to investigate things under the concession that some, or even all, aspects of knowledge of the real world is subjective in the sense that the extramental world can be cognitively approached only instrumentally (that is, with instrumental signs only). And this renders concepts such as ' isomorphism ', ' model ', etc., very important.
But alongside this assumption that the extramental world can be cognitively approached only instrumentally, the alternative option -- all knowledge can in principle be(come) objective -- (as is held by intentional Logic), can still be entertained and held plausible according to the following lines :
Only in sensory observation there is a direct contact of the knower and the extramental world, and this in virtue of the coding-decoding process as described earlier. Formal contents of the outside world are present in the knowing power in the form of high-level brain features. First of all these are the empirical concepts, concepts consisting of the implicit predication of such a formal content of all the individuals of the concept's extension. This implicit predication embodies the concept's signifucation.
A subject predicate-proposition consists of concepts. Each concept has its signification. The truth of the proposition depends not only on the signification of its concepts but especially on their designation. If the designation of the concepts in the proposition is such as to effect an isomorphy between the proposition -- as sign -- and the relevant segment of the extramental world, where this relevance is determined by the signification of the concepts, then the proposition is true. And indeed, only when there is such an isomorphy the subject-predicate proposition actually intends.
In all this we must realize that for a proposition to be a genuine logical intention it must first of all be a subject-predicate proposition because its explicit relation of identity, as it reflects the relation of identity between things and concepts ( = implicit predications), is a first condition of knowledge to be objective. But then, still such a subject-predicate proposition could be false, because of failure of, or wrong, designation of its terms. Only when the designation is right, that is, when it effects isomorphy, the proposition really intends, i.e., it then is a genuine logical intention. That is to say, then not only the constituent concepts are logical intentions, but also the whole proposition.
Precisely the same holds for arguments, because they solely consist of propositions. In order to be a logical intention an argument must first of all consist of subject-predicate propositions, but in addition to that, the designations of all the concepts figuring in the argument must be such that an isomorphy is resulting between the argument as logical entity on the one hand, and the causal structure it is supposed to represent on the other.
And because in the case of propositions, as well as in that of arguments, in all probability such isomorphies can in principle be accomplished by the knowing power, all knowledge of the extramental world can in principle be objective.
These two lines of approach, viz.,
Resumption of the exposition of 'the argument' as logical instrument.
Compound propositions and their relevance to the topic of argument.
The objects intended by compound propositions.
The categorical proposition -- that is, a proposition that is asserting something without conditions -- is the final and perfect instrument of knowledge. It is designed to (or should we say, it has biologically evolved as to) represent both that things ARE and WHAT they are, nor would we seem to require more for knowledge and understanding. But, until a proposition is seen to be true, we cannot be sure whether it represents things as they really are, nor is the truth of a proposition always, or even usually, self-evident. Instead, evidence must be provided from outside that proposition itself, and such evidence, as we have seen, always takes the form of other propositions which are supposed to have bearing on the proposition to be proved ( VEATCH, p.332 ). Here, then, would seem to be the real ground for bringing other propositions into combination with a given proposition. In this way we have the syllogism, consisting of three subject-predicate propositions. And now we see what compound propositions really can be : A compound proposition is a proposition in which several propositions are combined into a single one. And of course such a combination could in fact be a whole argument compressed into the form of a single compound proposition. As we shall see presently, all so-called hypothetical propositions are really syllogisms or at least involve syllogisms. Therefore, those compound propositions that are hypothetical propositions always intend some cause-effect situation in extramental reality (while, as we will see, compound propositions of the conjunctive type intend accidental coexistence in extramental reality).
In mathematical Logic the compounding of propositions is treated of in the so-called propositional calculus. There, all the connective constants such as AND (conjunction), IF-THEN (implication), OR (disjunction), but also constants such as NOT (negation), are being investigated. But in contrast to how such compound propositions are treated of in intentional Logic, in mathematical Logic their truth values are made dependent on the truth values of the component propositions. They are laid down as rules in so-called truth tables. For instance, the truth table for compound propositions in which the component propositions are linked together by OR (resulting in a disjunctive compound proposition) is :
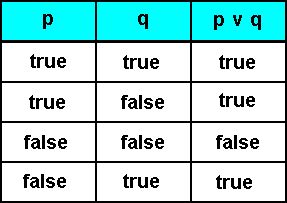
where ' p ' and ' q ' are propositions, and 
the compound proposition : ' p or q '.
This is the ' inclusive "or" '.
Another way to define OR is the ' exclusive "or" ' :
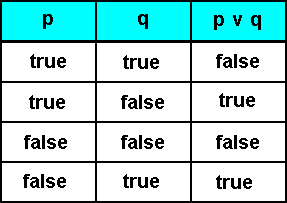
Here the proposition p v q becomes implicative, because we have : either p or q but not both. So if we want p, then we must not have q, and if we want q, we must not have p.
For everyone of the above mentioned logical constants (and, or, if-then, not) there is a truth table. The treatment is fully non-intentional, and it will turn out that all the theorems of the propositional calculus are (compound) propositions that say something, not of things, but of propositions, for instance that a certain proposition can also be expressed in another way and still meaning the same thing. So here, in mathematical Logic, compound propositions are treated as syntactical entities, without them having any intentional function at all. It is just an independent calculus where propositions are linked together and compounds are rearranged, all of it according to certain rules. We will return to the propositional calculus of the mathematical logicians later.
On the other hand, in an intentional Logic such connections, etc. are differently treated : It is asked what precisely in extramental reality (or a reality just taken as if it were such a reality) is intended by a given (type of) compound proposition.
Compound propositions are either categorical or hypothetical, or they are conjunctive, disjunctive, or implicative.
A categorical proposition, that is, an unconditional proposition, can be a simple, that is, not compound, proposition -- then it has a simple subject-predicate structure : S is P. If not explicitly analysed (into subject, copula, and predicate), such a proposition can be called p, and another such proposition can be called q, and yet another one r. As such, that is as p, q, and r, they are elements of compound propositions, and also for the propositional calculus they are the basic elements, the logical atoms.
In addition to single propositions being categorical, there are compound propositions that are also categorical. First of all these are the conjunctional propositions. A conjunctional proposition is a proposition that consists of several single propositions linked by AND. When we symbolize the connective constant AND as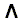 
we can have the compound proposition 
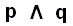. Here we have just a set of two categorical propositions p, and q.
Examples :
.
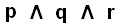But there are other compound propositions that are categorical, while not being conjunctions : causal propositions and concessive propositions.
Causal propositions begin with ' since ', ' because ', ' consequently ', ' therefore ', etc. As an example :
Because an agreement was made with Hitler, the British did not declare war on Germany.
In this compound proposition it is categorically stated that there was made an agreement, and that no war was declared. So this compound proposition is categorical. However, the second proposition is clearly made dependent upon the first, that is, the second follows upon the first. Were the first not true, then war was declared. So here we do not have to do with the intention of an accidental togetherness or coexistence of two things or events. Accordingly, this compound proposition is not a mere conjunction (of propositions).
The second type of categorical compound propositions which are not conjunctional are the concessive propositions. They are characterized by expressions such as ' although ', ' still ', ' nevertheless '. Example :
Although the British could not directly engage the Germans in Poland, they did declare war on Germany.
Here also, it is categorically stated that the British were not in a position to engage the advancing German army in Poland. And also it is categorically stated that war was declared on Germany. So this compound proposition is categorical. In this proposition an implication is denied :
If the British cannot directly engage the Germans in Poland, they will not (yet) declare war on Germany.
And because the implication is denied, a concessive proposition is just some sort of conjunctive proposition : British could not engage AND British declared war. But of course the two component propositions of our original concessive proposition are not propositions that have in fact nothing to do with each other like in genuine conjunctive propositions.
So not only are conjunctive (compound) propositions categorical, but also causal (compound) propositions and concessive (compound) propositions.
Causal (compound) propositions are implicative, that is, the second proposition in such a compound proposition is an implication of the first : ' because p, q '.
A concessive (compound) proposition is, we could say, also implicative, but here the implication is denied. ' Although p, (nevertheless) q '.
Conjunctive (compound) propositions are clearly not implicative.
So far for categorical compound propositions.
Compound propositions that are not categorical are hypothetical propositions, that is, are assertions depending on some condition. All hypothetical compounds are implicative in character. Hypothetical compounds contain two types : conditional (compound) propositions, and disjunctive (compound) propositions.
Let us give an example of the first type, viz., a conditional proposition.
If Germany attacks Poland, then the British will declare war on Germany.
Here it is not categorically asserted that Germany is attacking Poland, nor is it categorically asserted that the British will declare war on Germany. So this compound proposition is not categorical. As has been said, the two component propositions are not assertions. What is asserted is the necessary connection between the two component propositions. The second necessarily follows from the first : The Germans attacking Poland has as its consequence (as is asserted by the compound proposition) that the British will declare war on them.
The second type of hypothetical (compound) proposition is the disjunctive proposition :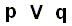 
(and, of course, also 
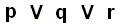etc.), that is, 'p or q', 'p or q or r', etc. Example :
Germany will either be brought to its knees by a blockade or by military attack.
Here it is not categorically asserted that Germany will undergo a blockade, nor is it categorically asserted that it will undergo military attack. So this compound proposition is not categorical. The two parts of the compound depend on each other (as to their truth) (we here think of the exclusive 'or' ) : When Germany will unergo a blockade, it will not be subjected to military attack. But when it will be subjected to military attack, no blockade will be set up against it.
Implicative (compound) propositions involve syllogisms.
On the other hand, there are also causal propositions which intend a general causal relation, such as
Because towels have a capillary structure, they are absorbent.
Also this is an abbreviated syllogism, but now one that proceeds from general to special :
If the British cannot directly engage the Germans in Poland, then they will not declare war on Germany.
A conditional ( = hypothetical) proposition expresses uncertainty. It expresses the uncertainty of the minor premise in the corresponding categorical and causal proposition :
Because the British cannot directly engage the Germans in Poland, they will not declare war on Germany.
This is a categorical (causal) proposition.
Our original proposition was hypothetical, rendering the minor premise of the above categorical syllogism uncertain. So this premise must be removed. As a result the conclusion also vanishes, and only the major premise ' if the British cannot directly engage the Germans in Poland, then they will not declare war on Germany ', is left, which was our original proposition.
The above hypothetical proposition was about a particular causal situation, and expressed uncertainty.
There are also hypothetical propositions that are about general causal structures and express uncertainty, such as :
If towels have a capillary structure, then they are absorbent.
It is an abbreviated syllogism that results from the corresponding causal, and therefore, categorical, syllogism when its minor premise is uncertain.
First the categorical syllogism (already given earlier) :
We have given a few examples showing in what way implicative (whether categorical [and thus either causal or concessive] or hypothetical) propositions involve syllogisms. Nevertheless, it must not be supposed that a hypothetical is always just a simple enthymeme, that is, an abbreviated syllogism, requiring nothing but the explicit assertion of either a major or a minor premise to yield a complete syllogism. On the contrary, the hypothetical proposition may be an abbreviation for a whole sorites or series of syllogisms. On account of this, it sometimes requires no little ingenuity to elaborate such a hypothetical proposition so as to make explicit all of the syllogisms and all of the middle terms that are implicit in it. Veatch, p.341, gives an example :
We are faced with the following hypothetical proposition :
If the value of gold is determined by the amount of labor necessary to produce it, then improvements in mining machery will tend to increase prices.
(the consequent means that if gold becomes cheaper you need more of it in order to get money, that is, you need more money to buy things).
Expanded into its complete form, this conditional proposition may be seen to involve two syllogistic arguments, the one being an argument in support of the minor premise of the other.
Correspondingly, no sooner is the hypothetical character of the antecedent clause of a conditional proposition removed, than the conditional proposition itself is replaced by a regular categorical syllogism. This is illustrated in the familiar cases of modus ponens, such as : If virtue is knowledge, it can be taught. Virtue is knowledge. Virtue can be taught, and modus tollens, such as : If virtue is knowledge it can be taught. Virtue cannot be taught. Virtue is not knowledge.
The two just mentioned syllogisms can both be derived from the following hypothetical proposition ' If virtue is knowledge, it can be taught ', by removing the uncertainty of either the antecedent or the consequent. And this is done by asserting respectively : ' virtue is knowledge ' and ' virtue cannot be taught '.
Let us make matters more clear by systematically considering this hypothetical proposition and the respective derivations of the syllogisms one at a time :
If virtue is knowledge, it can be taught.
In removing the uncertainty of the antecedent, we say : virtue is knowledge.
But then the consequent immediately follows. So we now have the modus ponens syllogism :
The same hypothetical proposition
If virtue is knowledge, it can be taught,
can be transformed in to a modus tollens syllogism by removing the uncertainty not of the antecedent, but of the consequent, namely by flatly denying it : Virtue cannot be taught. But then the antecedent cannot be true, because when it were true then the consequent could not be denied. So we now have the modus tollens syllogism :
The two syllogisms are often called "hypothetical syllogisms", because the major premise is stated hypothetically. But because the minor premise has removed this hypothetical character, the syllogisms are in fact categorical. That this is so can be seen if we transform (without changing the meaning) the modus ponens into a straight categorical syllogism, that is, if we transform
And now for the modus tollens :
We transform (and the meaning staying the same)
VEATCH, p.343, remarks that one might retort along the following lines : "Surely, even if some conditional propositions must be admitted to be really syllogisms, surely not all of them are such. Consider the proposition, ' if anything is a man, it is mortal '. Here surely is no syllogism but only a universal categorical proposition, ' all men are mortal ' ". Indeed, just as the mathematical logicians have argued that universal categorical propositions are really conditionals, so also many latter-day Aristotelians have argued that such conditionals are really universal categoricals.
Our exposition of the involvation of syllogisms in implicative propositions is far from complete (for more about it, see VEATCH, p.339-344). It just shows the way how to think about such propositions from the point of view of an intentional Logic.
Transitivity is not a logical pattern embodying a type of inference in certain arguments, but is a real relation between real entities.
The mathematical logicians hold that it is not the syllogism alone that is a pattern of logical inference, but that there are many patterns of logical inference, one of them being transitivity. For instance, we not only have inferential patterns such as
Here we will use the relation ' congruent to ' which, just like the relation ' outnumbers ', and the relation ' greater than ' (and also the relation ' is ' [that is, the relation of identity] ), is a transitive relation (we choose this relation, because it happens to be well worked out by other authors).
We then can have the following inference :
Nevertheless, since, as we have seen, any hypothetical proposition is really an enthymeme ( = abbreviated syllogism) with a categorical major premise suppressed, any such modus ponens argument as the one just presented is unmistakably a syllogism. And indeed the hypothetical major premise of this modus ponens argument certainly presupposes, and doubtless is itself but a disguised categorical proposition asserting the property of transitivity of a certain type of unity of order, as soon as we remove the uncertainty whether there is such a unity of order. And it is in the minor of the above modus ponens argument that the existence of such a unity of order is explicitly asserted : ' items a, c, and b are elements of S such that a is congruent to c and c to b '.
Accordingly, following through with these considerations, we come out with a syllogistic argument of this type :
Or, if we wish to make a itself the subject of our conclusion, we could state the argument thus :
In both cases we have genuine syllogistic arguments.
To be sure, in order to prove that a was congruent to b, it was necessary to take into account the nature of the relation of congruence (or more accurately, of the concrete unity of order constituted by such a relation), as well as the fact that such a relation (or unity of order) by its very nature has the property of transitivity. Yet this by no means indicates that the transitivity of the relation of congruence provides the form or structure of the inference itself, or that the inference is for that reason asyllogistic.
Quite the contrary, the nature or essence of the relation (or unity of order) is the real cause of the property of transitivity, and it is this causal order in reality (whether mathematical reality or material reality) which is intended by and provides the foundation for the demonstration. Still the form of the demonstration is syllogistic, involving the relation of triple identity. Indeed, the same considerations would apply in regard to all of those transitive relations of which the mathematical logicians have claimed to provide examples of nonsyllogistic inference, viz., ' greater than ', ' north of ', ' earlier than ', ' simultaneous with ', ' equal to ', etc. In short, transitivity, instead of being the form or pattern of the inference, is rather the real fact upon which the inference is based.
Thus, when we say that a is congruent to b, the real relation here is one of congruence, but the logical relation by which we know this real relation is one of identity between subject (term) and predicate (term). So in the proposition ' a IS congruent to b ', ' a ' is the subject, ' is ' is the copula, and ' congruent to b ' is the predicate. And this subject-predicate proposition intends the real relation of congruence between the real item a and the real item b. As such this subject-predicate proposition signifies formally, that is, as a formal sign, the real relation. And, again, as such it is a genuine logical intention.
On the other hand, this same real congruence between a and b can also instrumentally be signified, namely by the proposition ' a IS CONGRUENT TO b '. In this latter proposition ' a ' is a term, and ' b ' is a term, and these terms are connected by ' is congruent to '. But now such a proposition is not intentional anymore.
Likewise, when we ask why a is congruent to b, we find that the answer can only be in terms of what a is : it is a certain part of a particular kind of unity of order, and also in terms of what such a part is : it is such as to be congruent to a certain other part, c, which itself is congruent to b. In short, here is the familiar relation of triple identity, and therewith the demonstration of the proposition to be proved (VEATCH, p.353 ). The propositions in the syllogistic argument proving a to be congruent to b have IS (or some other form of the verb ' to be ' ) as copula. Before the copula there is the subject, and after it the predicate :
Other properties of relations besides transitivity, and their supposed relevance to inference.
But, according to the mathematical logicians not only transitivity is a form of inference, but also some other relations. The following examples are instances of inferences having the form of conversions. Here it thus is the property of convertibility that is supposed to be yet another form of inference :
Or the proposition about a being north of b can be interpreted as :
An intentional Logic always holds to the second interpretation, that is the interpretation of the proposition such that it is a genuine logical intention, and for it to be such an intention it must be a subject-predicate proposition, i.e. a proposition involving the peculiar relation of identity between predicate and subject. But then intentional Logic cannot account for the inference
The same goes for all other relations that are supposed to represent forms of inference, like ' symmetry ', ' one-to-one ', ' one-to-many ', ' many-to-one ', etc.
All of them are real properties of real relations or unities of order.
It should now be clear what the true import is of the relational calculi of the mathematical logicians. That such calculi are a remarkable achievement goes without saying. Indeed, they offer nothing less than an ordered and systematic presentation of all sorts of different kinds of relation, together with their many and varied properties. Yet to suppose that such relations and relational properties provide us with just so many forms of logical inference involves a serious confusion of real relations with logical relations. And while these real relations and their real properties are entirely appropriate as objects of intention, the actual intention of them can only be achieved in and through the peculiarly logical relations of identity ( VEATCH, p.357/8 ).
Transitivity once more.
Having discussed the transitivity of relations such as ' is congruent to ', ' is greater than ', ' outnumbers ', etc., it is now time to consider the transitivity of the relation ' is ' as it figures in syllogisms.
Couldn't it be that the inference as we see it in genuine syllogisms is based, not on the (triple) identity, but on its property of transitivity? For, surely, the relation ' is ' is transitive. And, indeed, were it not transitive, we would have no inference in a syllogism. In mathematical Logic it is held that indeed the inferential character of a syllogism is totally based on the transitivity of the relation ' is ', that is the relation of identity. And not only the syllogism is an instance of transitivity but also, as we have seen, certain nonsyllogistic arguments such as :
The transitivity as being a property of (certain) real relations -- let us call such relations "Q" -- can be demonstrated by the relation of identity " I " :
[ I ] transitivity (of Q)
The transitivity here is not the form of the demonstration. This form is I.
The transitivity as being a property of the intentional relation of identity ( I ) can be demonstrated by a second order relation of identity ( I ' ) :
[ I ' ] transitivity (of I )
Also here the transitivity is not the form of the demonstration. This form is I '.
The argument for the transitivity of a given so-called equivalence relation (such as congruence, or identity) R uses the reflexivity of the relation R : xRx, and the property -- let us call it P --
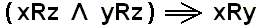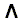. = the connective "and",
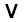= the connective "or",
= the implicative connective "if-then", 
= the equivalence connective or double implication "is equivalent to", and
The transitivity is then symbolized by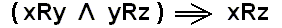 
.
The proof of the transitivity of a relation R which is reflexive ( = any element stands to itself in this relation), and such that property P holds, that is, that any two elements of the relevant set of elements both standing in this relation to a third element of this set, do also stand in that relation to one another (which, together with the reflexivity of the relation, makes the latter symmetric : xRy = yRx), is expressed in mathematical Logic as follows (where xRy means : x is related to y according to the relation R ) :
Axiom I :
For any element z of the set S, zRz.
Axiom II :
For any elements x, y, and z of the set S, if xRz and yRz, then xRy.
Derivation of Theorem I :
zRz (according to Axiom I)
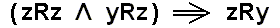(according to Axiom II)
From this it follows :
, from which in turn follows :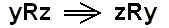 
(is Theorem I, property of symmetry of the relation R ).
Derivation of Theorem II, which asserts the property of transitivity of the relation R :
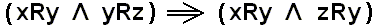(according to Theorem I ) and
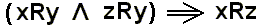(according to Axiom II ),
and, applying again Theorem I we get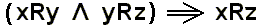 
, which is the property of transitivity of the relation R.
In this derivation of the transitivity of a relation R we don't see any relation of identity making up the form of the inference. In order to show that this is simply caused by the notation and way of expressing things in mathematical Logic, we give this proof once again. But now in this (version of) proof the subject of its various propositions is not one or another element, nor the relation R abstractly taken, but the whole relational complex, consisting of certain elements x, y, z, etc., elements, as we know, of such a nature that the relation R is relevant to them. So, again, the subject of the propositions (together forming three syllogisms) is a unity of order or relational complex. And of this subject things are asserted.
Accordingly, in Axiom II for example, the expression
( For any elements x, y, and z of the set S ), if xRz and yRz
is not a proposition, but a complex concept designating a unity of order in which xRz and yRz. And of this unity of order it is asserted (in the Axiom) that xRy, as being a property of that unity of order.
So we have a relational complex or unity of order, which we call R because the relation R, on which we focus, and which is supposed to obtain between its elements x, y, and z, etc., is relevant (for example the relation of congruence is relevant for a unity of order consisting of line segments). Of this relational complex R we can predicate things. For instance, we can say that for any element x of R, x stands in the relation R to itself, and we denote this by the proposition ' R is xRx '.
Generally, when in R two elements x and y relate to each other by the relation R, we denote this by the proposition ' R is xRy '. And when for any elements x, y, z our unity of order is such that, say, xRy ==> zRy, we predicate ' R is xRy ==> zRy '. In all these propositions ' R ' ( = unity of order) is the subject, ' is ' the copula, and all what comes after ' is ' is the predicate.
Working one (more) example fully out :
"R is 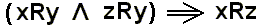" MEANS :
The unity of order R is such that if element x is related by the relation R to element y, and element z is related to element y according to the same relation, then element x is related to element z by that same relation.
We can now give the argument that R is a transitive relation if R meets two conditions, namely when it is reflexive, and when two elements, when being both related to the same element by the relation R, are then related to each other also by the relation R (this is the property P mentioned above).
We have the unity of order R, characterized by the relation R as being a possible and relevant relation between elements of R.
First syllogism :
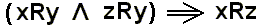(property, set for the relational complex R ).
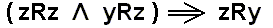, that is :, that is,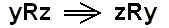 ( = property of symmetry).
.
.
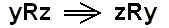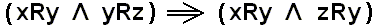Third syllogism :
.
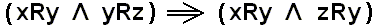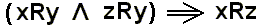(according to the above properties set for the relational complex R ).
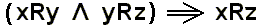, which means that the relation R is transitive.
The relation of ' congruent to ' has the properties as set for the relation R, and consequently it is a transitive relation. But there are other relations, such as ' greater than ', which do not have these properties (only equivalence relations do have them : reflexivity and symmetry), but are nevertheless transitive.
In the next document we will continue our exposition of argument.
e-mail :
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for further study of Logic, Part VII.
Back to Aristotelian metaphysics Part I
Back to Aristotelian metaphysics Part II
Back to Aristotelian metaphysics Part III
Back to Aristotelian metaphysics Part IIIa
Back to Aristotelian metaphysics Part IV
Back to Aristotelian metaphysics Part V