

e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam ) In the previous document we have started the exposition of the second major division of intentional Logic, Propositions. The present document continues this exposition.
Overview of the Problem of the Null Class and its Solution in terms of an Intentional Logic.
Intentional Logic holds that all true subject-predicate propositions (S-P propositions) must have existential import, in the sense that they must designate their subjects as existing (in one way or another). Indeed, it is the copula that expresses this existence.
But what to be done with propositions that involve the so-called null class, that is, propositions that lack any designation of their subject term?
For example, take the proposition :
all sea serpents live in the Atlantic.
Here the subject term is without designation, because sea serpents do not exist (and have never existed). Because lacking designation the proposition can be considered false. But then also its contradictory opposite is false, because it too lacks designation :
some sea serpents do not live in the Atlantic,
(where "some" means : at least one ).
Contradictory opposites tolerating each other in possessing the same truth value, such as we have here (affirmative proposition false ==> contradictory opposite false), is logically inadmissible, because a proposition must be either true or false. And if it is true, its contrdictory must be false, and if it is false, its contradictory opposite must be true.
The solution of this dilemma as proposed by modern Logic, is to stipulate that universal propositions (such as ' all men are mortal ,' [or, equivalently, ' man is mortal ' ], ' all sea serpents live in the Atlantic ' ) do not have (any) existential import. This is said to be shown by the following conversions of such propositions, taking the two just mentioned propositions as an example :
all men are mortal
is converted into:
no man is not mortal,
So here, even when there are no human beings at all, that is, even when the subject term ' man ' fails to designate anything, this proposition still makes sense, and could be true.
all sea serpents live in the Atlantic
is converted into:
no sea serpent does not live in the Atlantic.
Also here, the fact that there are no sea serpents at all, that is, even when the subject term ' sea serpents ' fails to designate anything, this proposition still makes sense, and could be true.
Thus it is now, according to mathematical Logic, reasonable to stipulate that universal propositions do not have existential import.
And now we cannot say anymore that the proposition ' all sea serpents live in the Atlantic ' is necessarily false, and is so because its subject term fails to designate : No designation (of existing individuals) is needed, because it is now stipulated that universal propositions do not have existential import (while particular propositions [still] do). So now the proposition ' all sea serpents live in the Atlantic ' could be true.
And now its contradictory opposite :
some sea serpents do not live in the Atlantic
is false, because, as a particular proposition it has existential import, and thus in fact says :
there exist some sea serpents (that do not live in the Atlantic).
And because there exist no sea serpents at all, the proposition is false.
And because the affirmative proposition could, as we just saw, be true, we do not necessarily have to do with contradictory opposites having the same truth value anymore, and the problem is solved. That is to say, by denying existential import to universal propositions (and affirming it with respect to particular [and singular] propositions) the problem of the null class is solved by modern Logic.
However, for an intentional Logic such a solution is unacceptable because intentional Logic holds that every genuine proposition must have existential import. It is this import that distinguishes it from mere concepts. Existence, however, comes in different senses : actual, potential, real, existing-only-before-the-mind, etc., but are existence nonetheless.
And if a subject of a proposition is able to designate existents, there will be no problem with the truth values of contradictory opposites (and with all other inferences based on the traditional square of opposition -- [see below] ), provided we keep the same designation. That is, when we go from a proposition to its contradictory opposite we must maintain the same designation. So when a proposition designates, say, (only) potential existents (and thus no actual existents) its contradictory opposite must also designate potential existents (and no actual existents).
So far, so good.
But, granting that universal propositions do have existential import, and that existence can come in several different senses, what about null classes?
The proposition ' all sea serpents live in the Atlantic ' doesn't seem to designate anything (because sea serpents do not actually exist). So also its contradictory opposite, implying that both must be considered false. But here we can remedy this problem, namely by holding that 'sea serpents', although not actually existing in extramental reality, do exist as beings of reason. And as such the proposition ' all sea serpents live in the Atlantic ' could be true, and its contradictory opposite false. But this is silly, certainly in the context of propositions expressing knowledge. A proposition like ' all sea serpents live in the Atlantic ' should be such as assuming to refer to actual real existents, of which something is asserted. But there are no sea serpents existing at all, so the designation that was meant does not match with the real designation. So the proposition must be false. But then its contradictory opposite is true for the same reason : ' some sea serpents do not live in the Atlantic '. Here also the subject term is meant to designate actual, real, existents, while in fact the term designates only beings of reason. Therefore we can deny sea serpents living in the Atlantic as (this denial is) expressed in the contradictory opposite. So in this example we do not have a problem : Failure of designation makes the affirmative proposition false, and its contradictory opposite true ( Indeed, the proposition ' some sea serpents do not live in the Atlantic ' is perfectly true : Because there are no sea serpents at all they do certainly not live in the Atlantic).
What about the designation and existential import of our proposition ' all sea serpents live in the Atlantic ' ? Well, whether there is or is not such an import and designation, depends totally on how the proposition is meant (by the enunciator). And, if it is to convey knowledge, the subject term is meant to designate actual, real, existents. So this is the designation. And as such this proposition has existential import.
However, this is not all. That is, the problem of the null class is still not totally solved, because there are propositions that are such as only to allow some definite designation, say, designation of actual, real, existents (or an existent). So, for example, the (famous) proposition :
the present king of France is bald,
an example of RUSSELL. Here the expression ' present ' allows for no other designation than that of an actual, real, existent. But there is no present king of France. This means that the subject term does not designate anything whatsoever. So the proposition must be false, because of a failure of designation.
And what about its contradictory opposite
the present king of France is not bald ?
(Here we cannot say that this is equivalent to :
there is no present king of France who is bald
[which could be true even if there is no present king of France, while its contradictory opposite is false because of the failure of designation] : We cannot say this [and thus not have the solution in this way] because ' there is no present king of France who is bald ' means that of all the present kings of France no one is bald, which is clearly absurd).
Well, also in the proposition ' the present king of France is not bald ' the expression ' present ' forces the designation to be of an actual, real existent, and nothing else. But because there is no present king of France, also here the designation fails completely, rendering our contradictory opposite false.
So here we have a genuine null class, and a real dilemma.
The solution of the intentional logician can be roughly sketched as follows : The subject term does not designate anything whatsoever. And this means that the statement ' the present king of France is bald ' is not about anything. Therefore this statement is not a genuine proposition at all.
Although already roughly having outlined the solution, we must -- if we want to go to the bottom of the problem -- still ask the question : How is an intentional logician, with his theory of designation, where all universal propositions have existential import, going to deal with the null class? That is, how must he logically evaluate propositions that involve the null class? If he follows modern (mathematical) Logic, he must hold the principle that says that no universal proposition has existential import : only particular and singular propositions do have such an import. This, as has been said, is unacceptable for intentional Logic.
So the intentional logician must show that in fact null classes are never involved in genuine propositions (and thus implying that all propositions, including universal ones, have existential import). And thus we must say that when apparently genuine null classes do appear in statements, these statements are not genuine propositions, because they are about nothing : Their subject term does not designate anything. So such statements must be ruled out of Logic altogether.
This is, in a nutshell, the problem in which the intentional logician finds himself, plus the lines along which he proposes a solution, while keeping his principle that genuine propositions have existential import (in contrast to mere concepts).
The Null Class and its solution in terms of an Intentional Logic.
We will now work all this out in detail.
The scheme of the ensuing discussion is as follows :
We will adress these four points one by one in the following.
1. There is existential import not only for particular propositions ( ' some men are wise ' ) and singular propositions ( ' Socrates is wise ' ), but also for universal propositions ( ' all men are wise ' ).
The transformation by mathematical Logic of singular and particular propositions into conjunctions, and universal propositions into hypotheticals, in order to pin down the designation of the subject term.
In modern mathematical Logic one holds that the concept, as expressed in the subject term of a proposition, must itself be further analysed into a relation of subject to predicate. But this further analysis is in fact just the explicit application or employment of the concept : The concept possesses already within itself a relation of identity to relevant individuals. The motivation of the mathematical logician is apparently that he assumes that to characterize individuals by a universal concept could only be misleading and would certainly require further analysis. For instance, to call an individual a human being would really be but a concealing or a blurring of the real relation between that individual and one of its attributes, viz., that of being human. Hence to remove all ambiguity and to bring into the open the actual situation of an individual being in relation, it would seem necessary to analyze the concept MAN, as it is applied to an individual, and to turn it into a proposition of the form ' x is a man '. But the mathematical logicians must do this because they do not recognize that the concept itself is already a relation of identity to the individuals of its extension. And the result of their analysis has, it is true, the form of a subject-predicate relation, but is not interpreted as involving a relation of identity, but rather a real relation between a substance and its attribute.
But the motivation of the mathematical logician could be different and maybe more to the point.
Concider the assertion ' that man is tall '. Presumably such a statement could be challenged not merely on the ground of the man's not being tall, but also on the ground that it was not a man at all. Apparently, here one is not merely affirming a predicate ( ' tall ' ) of a subject ( ' that man ' ). One is also, so to speak, affirming the subject itself, i.e., not just that the man is tall, but also that it is a man.
So the correct interpretation of the above proposition ( ' that man is tall ' ) would seem to be :
there is an x, such that x is a man, and x is tall.
The proposition ' that man is tall ' is a singular proposition. But the same considerations apply to particular propositions such as ' there is a burglar in the house ', because that what the subject term designates is not only in the house (as asserted), but it could be not a burglar at all, but a cat, say. So we must also say here :
there is an x, such that x is a burglar, and x is in the house.
With a universal proposition, on the other hand, such as ' all men are mortal ' we do not need to analyze the subject term, because the predicate can only be applied to living beings, and man is one (kind) of them. It is applicable to all living beings, and in the proposition it is applied to all men. We can express this finding more generally : In universal propositions the predicate term applies to all individuals of a certain domain, so there cannot be doubt whether it be this or that, or these or those individuals that are said to be so and so.
It is true, as the mathematical logicians have urged, that certain propositions are such that their subject concepts, instead of being genuine subjects, are really predicates ( ' x is a man ' ), so that these propositions are in each case not just one proposition, but two, that is, a conjunction of two propositions.
But we should be equally insistent that by no means all propositions with determinate subject terms are to be so interpreted. In many cases the designation of the subject term is clearly determined by the predicate (as it was not so in the case of ' that man is tall ', because there are so many other things that are tall ).
In contrast to particular and singular propositions the mathematical logician does not interpret a universal proposition as being in fact a conjunction of two propositions, but rather as a hypothetical proposition. So the proposition ' all men are mortal ' is not interpreted by him as :
all x's are men and are mortal,
but as :
for all x's, if x is a man, then x is mortal.
Indeed, the designation of the subject term ' men ' in ' all men are mortal ' is clear as soon as we see this proposition as in fact being a hypothetical proposition.
So by interpreting singular and particular propositions as conjunctions, and universal propositions as hypotheticals, the mathematical logician unambiguously determines the designation of the subject term.
Accordingly, the upshot of this whole discussion would seem to be that the mathematical logician is simply mistaken about the subject-predicate proposition as such, that is, what it precisely and as such really, and generally, is. He is mistaken in supposing that if the full meaning or intention of a subject-predicate proposition, as single and categorical proposition, is to be disclosed, the subject term (and thus the concept which it expresses) must, in all cases, be analyzed out and made the predicate of a second proposition (either connected by an implication [if ---, then ---] or by a conjunction [--- and ---] ) -- as if the only proper subjects of propositions were individuals completely bare of conceptual characterization (completely stripped of formal content). For although some propositions do stand in need of such further analysis, by no means do all. As for those that do not, to insist upon subjecting them to such analysis is thoroughly misleading, in that it tends to hide the fact that in their cases the predicate is attributed not just to some designata or other, but precisely to those of that specific subject concept.
As we have seen, the mathematical logician turns all universal propositions into hypotheticals and all particular propositions into conjunctions. As such this is logically legitimate. But it is, as has been shown, not generally necessary. It might be necessary for a singular proposition such as ' there is a burglar in the house '. But such propositions do not convey general knowledge, but only particular states of affairs.
On the other hand, for propositions that do convey general knowledge and insight, such as ' all men are mortal ', or ' some men are wise ', there is no need to transform or interpret them into either hypotheticals such as ' for all x's, if x is a man, then x is mortal ', or conjunctions such as ' there is an x, such that x is a man, and x is wise ', because in such propositions the designation of the subject term is clear, and this subject term is therefore in no need of further analysis.
Moreover, a hypothetical (as a result of the transformation of a universal proposition) is in fact less fundamental than the original universal proposition, because such a hypothetical is really an enthymematic syllogism.
Consider the following syllogism :
All organisms are mortal, all men are organisms, therefore, if x is a man, then x is mortal.
So our hypothetical proposition is in fact the conclusion of a syllogism. In fact, from ' all organisms are mortal ' and ' all men are organisms ' directly follows : ' all men are mortal ', and having this, we can immediately say : ' for all x's, if x is a man, then x is mortal '. So the hypothetical proposition presupposes the corresponding categorical universal proposition.
Now for conjunctions.
Particular propositions are interpreted by the mathematical logicians as conjunctions. For example, the proposition ' some men are wise ' is interpreted as ' there is an x, such that x is a man, and x is wise '.
However, this second proposition (or conjunction of propositions) does not represent an analysis of the first, in the sense that it expresses clearly what the first had expressed only confusedly. If it is recognized that a concept is a relation of identity to individuals, and also that in a proposition the concept actually designates these individuals as existing, then it is not necessary to represent the relation between a concept and its designated existents by explicitly predicating the concept of them. To be sure, the concept is predicable of them, but actually to predicate it of them constitutes not an analysis of that concept, but rather a further use or employment of it ( VEATCH, p.242 ).
Existential import.
Because, according to the mathematical logicians, universal propositions are really hypothetical propositions, they do not assert existence. Thus, whether any human beings actually exist or not, is quite irrelevant to the assertion ' if anything is human, it is mortal '.
But, also according to the mathematical logicians, things are different with respect to particular propositions : If there were no human beings, one could hardly assert that some beings are human and are wise, which is the way the mathematical logician would interpret ' some men are wise '.
Hence the supposition that particular propositions assert existence, whereas universals do not.
However, as we have seen, for propositions conveying general knowledge, they are not to be interpreted as either hypotheticals or conjunctions. So the sharp difference in existential import between universal and particular propositions disappears.
Indeed, when we acknowledge the fact that existence can come in several ways (potential, actual, real, fictitious) we see that universals are particularly adapted to designate potential (in the sense of possible) existents. So when we say ' dinosaurs are living mainly in warm regions ', the subject term designates (exclusively) possible existents. But the designation of universal propositions is not in every case confined to mere possible existents. For example, consider again the (universal) proposition ' all men are mortal '. Here the designation includes possible as well as actual existents. And it is indeed in most cases that actual existents are designated by universal propositions, for example ' all presently living sponges are inhabiting natural waters ', and even more clearly : ' all helium atoms are to have two protons in their nucleus '.
So universal propositions do have existential import, often designating even actual existents.
Now for particular propositions (concentrating on those that convey general knowledge).
According to the mathematical logicians they have existential import (also according to intentional Logic). But because they do not seem to recognize any form of existence other than actual, real, existence, they say that particular propositions exclusively and always, designate actual, real, existents. True, particular propositions (such as ' some men are wise ' ) are peculiarly fitted for the intention of actual existence (just as universal propositions are for the intention of possible existence). But just as the subjects of universal propositions may often be used so as to designate actual existents, so also the subjects of particular propositions may be used to designate merely possible existents. Consider the proposition ' some dinosaurs are warm-blooded '. Here the subject term designates mere possible existents.
So particular propositions do not exclusively, and in all cases, designate actual existents, sometimes they designate possible existents.
So from all this we can conclude that particular as well as universal propositions do have existential import. And this is fully in line with the tenets of an intentional Logic, which holds that propositions, in contrast to mere concepts, always have existential import.
But having established this, we realize that it will now be a big question as to how logically evaluate all cases of propositions which involve the null class. That is to say, how from an intentional point of view we should interpret propositions involving the null class, or, again differently expressed, how the theory of designation can cope with the null class, and whether it can do that better, or at least as good as, the quantification theory of modern mathematical Logic.
2. The thesis all propositions having existential import brings about the problem of the null class. This problem appears when the traditional square of opposition [see below] is considered (to be correct). We will expound this square now.
The traditional Square of Opposition.
The square of opposition systematizes the types of opposition obtaining between the four types of categorical ( = without conditions) subject-predicate propositions (A, E, I, and O), and lays down the rules of truth and falsity in oppositions (One such rule is, for example, that contradictory opposites cannot have the same truth value, that is, they cannot both be true or both be false).
It is these rules that are, according to the mathematical logicians, violated in some cases, to be precise in cases that involve the null class, depriving these rules of their general validity.
As such this looks suspicious.
We will show (largely following VEATCH, pp.249) that intentional Logic can restore things, by its theory of designation.
But let us first expound the traditional square of opposition (following BOYER, Ch., Handboek der Wijsbegeerte, I, 1947 [Dutch edition], p.115-119).
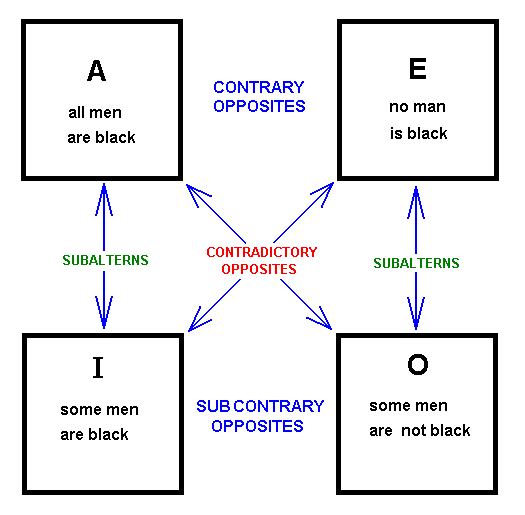
Diagram above : The Square of Oppositions.
In the above diagram "some" means : "one or another", or "at least one", etc.
The proposition ' all men are black ' is equivalent to ' every man is black '.
The proposition ' no man is black ' is equivalent to ' all men are not black ', and to ' every man is not black ' .
The diagram brings up four kinds of opposites :
Now we shall give the rules of truth and falsity implicitly expressed in this square.
The Square of Opposition under fire.
Consider the proposition
all the dimes in my pocket are shiny.
But suppose that actually there are no dimes in my pocket. If so, one might naturally feel that the A proposition which asserts that they are all shiny would be false.
Now consider the corresponding O proposition, that is, its contradictory opposite :
some of the dimes in my pocket are not shiny.
It is clear that also this proposition is false, in virtue of the same reason that the A proposition was false.
That the O proposition, which is a particular proposition, must be false, is moreover evident from the fact that it is assumed by the mathematical logicians that all particular propositions designate actual, and only actual, existents. And there are no dimes in my pocket ( We here have to do with the null class).
Having both the A and the O proposition false is a clear violation of one of the laws of truth and falsity as given above in connection with the square of oppositions. Indeed, even for a mathematical logician this ( = same truth value of contradictories) is inadmissible. So this problem, evoked by the null class, should be solved. How?
Well, by a re-interpretation of A propositions (whether they involve the null class or not). In what way are they to be re-interpreted? Obviously with respect to their alleged existential import.
So the mathematical logician now denies any existential import to A propositions (that is, affirmative universal categorical propositions) (while retaining it for particular propositions). He shows this by interpreting ' all the dimes in my pocket are shiny ' as :
there are no dimes in my pocket that are not shiny.
This later assertion, so it is argued, could be true even if there were no dimes in my pocket.
Generally, the mathematical logician interprets ' all S's are P's ' as ' there are no S's that are not P's ', whether there are null classes involved or not.
The particular proposition ' some dimes in my pocket are not shiny ' must be false (because, according to the mathematical logician, all particular propositions designate actual existents, and in this particular case there are no actual existents [in the domain indicated and delineated by the proposition] ). But because the corresponding A proposition, interpreted as ' there are no dimes in my pocket that are not shiny ' is true (indeed, when there are no dimes at all in my pocket, there can also not be dimes in my pocket that are not shiny), we now do not have two contradictory opposites (here A and O) having the same truth value. So a denial of existential import of A propositions solves the problem.
But this way of solving it not only goes against intentional Logic's contention that all genuine propositions have existential import, but also markedly disrupts the various relationships in the square of opposition :
According to the mathematical logician the A proposition ' all the dimes in my pocket are shiny ' is true (because he interprets it as ' there are no dimes in my pocket that are not shiny ' ). But then the corresponding E proposition, that is, its contrary, ' there are no dimes in my pocket that are shiny ' (which is supposed to be equivalent to ' no dimes in my pocket are shiny ' ) is also true. And according to the rules in the square this cannot be. Again a reason for the mathematical logician to abandon the square and its rules.
As has been said, in this new interpretation of A propositions the relations of contradiction would be preserved, since, given the truth of an A proposition involving a null class, the corresponding O proposition would have to be false, inasmuch as particular propositions are assumed to designate actual existents.
And also the truth of the E proposition ' no dimes in my pocket are shiny ' would involve the falsity of the corresponding I proposition :
some dimes in my pocket are shiny,
because also here we have a particular proposition, implying that actual existents are designated. But because there are no dimes in my pocket, the subject term fails to designate.
Having in our present case the A proposition true, and the I false, and likewise the E proposition true and the O proposition false, we see that the rules of subaltern propositions would no longer hold. (To recapitulate : according to the mathematical logician's new interpretation [universal propositions : no existential import, particular propositions : existential import, but only with respect to actual existents] the (exemplified) A proposition is true, precisely because there are no dimes in my pocket, therefore its contradictory opposite, the O proposition, must be false. By the same reason the E proposition is true, and thus its contradictory opposite, the I proposition, must be false.).
Also, having I false and O false the rules about subcontraries would have to be discarded.
O and I can both be true : ' some dimes in my pocket are not shiny ' (O), and ' some dimes in my pocket are shiny ' ( I ) : These latter shiny dimes are evidently different individuals from the ones in O that are not shiny. But they cannot both be false : If we suppose O to be false, then there are no dimes in my pocket that are not shiny. And if we suppose also I to be false, then there are no dimes in my pocket that are shiny. This is contradictory, so O and I cannot both be false. But in the new interpretation of the mathematical logicians we had both O and I false (showing that they can both be false at the same time). So also in this respect (subcontraries) the new interpretation clashes with certain rules of the square.
So generally we can say that the mathematical logician's solution of the problem of the null class (where the problem consisted in the violation of the rules for contradictory opposites [the only rules of the square that even the mathematical logician is not prepared to abandon]), namely his denial of existential import of A propositions, disrupts the relationships in the square of opposition. And for the mathematical logicians this is a clear sign that the Aristotle-oriented Logic is inadequate to deal with new propblems.
The mathematical logicians think that even from the point of view of Aristotelian Logic the square cannot be defended : Already we have seen how the Aristotelian logician, assuming as he does that A propositions must have existential import, proceeds on this basis to deny that an A proposition involving a null class could be true. But then he would also be forced to deny that its contradictory opposite could be true either (because ' some dimes in my pocket are not shiny ' cannot be true by reason of the fact that there are no dimes in my pocket).
However, anticipating solutions accomplished by intentional Logic, Aristotelian Logic does not get bogged down here because of the following reason :
The A proposition ' all the dimes in my pocket are shiny ' (that is, all the dimes ...) is not a proposition at all, because it not only involves a null class, but also at the same time has a definite description of the subject, namely ' all the dimes (present) in my pocket '. So the subject term is meant to designate actual existents and nothing else. But in fact there are no dimes in my pocket, so the designation fails completely (in the same way as it does in the proposition ' the present king of France is bald ', later to be discussed). Therefore the proposition is not about anything, meaning that it is not a proposition at all.
Only when we eliminate the definite description of the subject will the resulting proposition be a genuine proposition and will not pose a problem anymore because then no null class is involved anymore : So instead of ' all the dimes in my pocket ' (that is, instead of ' all those particular dimes that are in my pocket ' ) we take : ' any dime in my pocket ', and thus thereby remove the definite description. Indeed, ' any dime in my pocket is shiny ', asserts :
if there are dimes in my pocket, then they are shiny.
Here, obviously, even if there are no dimes in my pocket, or even if there never have been, the proposition still does not fail to designate, because all that is called for is a designation of possible existents and not necessarily of actual ones. And then there is no problem with the corresponding O proposition : The A proposition then is :
all possible dimes in my pocket are shiny,
while the corresponding O proposition (that is the contradictory opposite) reads :
some possible dimes in my pocket are not shiny.
Now, even when there are no actual dimes in my pocket, the A proposition could be true, and if it is (taken to be true) (in enunciating it I have in mind certain (or other) dimes that are potentially in my pocket [ I am about to receive them as a wage] and that are all shiny), then the O proposition is false, as it should be.
3. Restatement of the problem of the null class from the point of view of an intentional Logic (where all true propositions, including universal propositions, have existential import).
With the above discussion of the null class and its effect on the validity of the square of opposition we are presented with a whole parcel of considerations that must needs be appraised from the point of view of an intentional Logic.
Specifically, the issue would seem to be this : On an intentional view all true propositions must have existential import, in the sense that they must designate their subjects as existing (in some way or another). But what is to be done, then, with propositions which, as the mathematical logicians say, involve the null class? Surely such propositions would be lacking in designation and hence have to be considered false. At the same time, their contradictory opposites would have to be considered false too -- and this is certainly embarrassing. Accordingly, is an intentional Logic able to extricate itself from such a predicament?
By way of answer let us remark that the whole notion of the null class, which is often claimed to be a peculiar discovery of the new Logic, and which is certainly at the root of the present difficulty, is really a very fuzzy notion indeed. This is because, generally, in mathematical Logic, existence is taken univocally : With respect to the material world it is always considered to be actual, real, existence. So a class consisting of mere possible existents is considered to be a null class.
By the way, mathematical Logic (as well as intentional Logic) can also be about knowing mathematical objects. But these are then treated as if they were objects existing in extramental reality.
Sticking to (knowing) extramental reality, we then can have to do with a class that is a null class according to the mathematical logicians, while it is not so for an intentional logician. Corresponding to the different ways of existing we can have a designation of possible or actual existents. And when an intentional logician speaks about 'beings of reason' he does not mean mathematical objects (which he treats as real objects), but mere beings of reason, such as phoenixes, sea serpents, and te like.
Confronted with the mentioned difficulties, an intentional Logic can begin with seeing things as follows :
Take the proposition
all sea serpents live in the Atlantic.
Such a proposition the mathematical logician will regard as being an example of a proposition involving a null class (because sea serpents do not exist in extramental reality). They then show that the rules of contraries in the square of opposites do not apply to this example : For this to show they interpret
all see serpents live in the Atlantic
as
there are no sea serpents that do not live in the Atlantic.
This proposition is true (because there are no sea serpents at all).
And now its corresponding contrary :
there are no sea serpents that live in the Atlantic.
Obviously, also this proposition is true. So here we have an A proposition and an E proposition that both are true. But according to the rules in the square of oppositions contraries cannot both be true. So these rules should be abandoned because they are not universally valid.
What can an intentional Logic do about this situation (such that the mentioned rule does not need to be abandoned)?
Well, to begin with, intentional Logic holds that a proposition such as this one is about an existent something and does designate. True, the sea serpents which it is about, exist only as beings of reason. Still, such designation suffices for existential import, there is no null class. In consequence, the proposition is susceptible of either truth or falsity. The proposition is thus about some fictitious aquatic organisms about which it is asserted that they inhabit the Atlantic Ocean only. And whichever way one takes it, all the relations in the square of opposition will hold, provided only that one does not change the designation when one goes from A to E, or from A to O, etc.
If we now turn to the proposition
all the dimes in my pocket are shiny,
while there are no dimes in my pocket (and thus involving the null class), we see that, in all probability, this proposition is not about fictitious dimes, but is meant (and only that counts when evaluating the proposition) to be about not only real dimes but also of real dimes actually present in my pocket. But because there are no dimes in my pocket we now seem to have to do with the null class, and fail to designate altogether, with all of the perplexing consequences that apparently follow, so far as the square of opposition is concerned.
Even in the case of the sea serpents it could be that the proponent of the proposition (being not well at home in biology) actually meant real sea serpents existing in extramental reality. And then also here we have to do with the null class because there aren't any sea serpents existing in extramental reality.
In other words, the problem of the null class is simply not solved merely by pointing out that in addition to actual existents, terms in propositions can sometimes be taken so as to designate mere beings of reason (imaginary beings), because such a proposition could be meant to be about actual, real, existents, and when there are in fact no such existents, then we have a failure of designation. So how is an intentional logician, with his theory of designation, going to deal with the null class?
In his discusion about how to determine the correct designation in propositions involving the null class, VEATCH, pp.254, considers two propositions whose contradictory opposites do not involve a difference in quantity of the proposition (as this difference is present when we go from ' all S's are P's ' to ' some S's are not P's ' ) :
phlogiston is the cause of combustion,
and ( RUSSEL's celebrated example )
the present king of France is bald.
Both propositions involve the null class : There is no such substance as phlogiston, and there is no present king of France.
Are these propositions true or false? And what, precisely, is designated by their subject terms?
If we place these propositions in a purely fictitional context (where the old chemistry was the chemistry, and where France had a king), then there is no null class involved : The subject terms of both propositions designate, and designate exclusively, beings of reason or imaginary beings. And, having it all like this, there will be no problem with the rules of truth and falsity in the square of opposites.
But this (easy way out) is not what we want : We want that the proponent of these propositions supposes that they are about real actual beings. And now the null class is back again (because there is no phlogiston actually existing in extramental reality, and in the same way there is no present king of France).
So how about designation here, and what about their truth or falsity? Do they involve violations of some laws in the square of opposites?
Let us first consider ' phlogiston is the cause of combustion '
It is perhaps useful to know that in early chemistry it was thought that combustion involved some special substance called 'phlogiston'. But later it was found that the weight of all the chemical substances involved in combustion taken together was equal before and after combustion. So there is no special substance --different from the known chemical elements or compounds -- involved in combustion, that is, phlogiston does not exist.
If we take the term ' phlogiston ' in the proposition ' phlogiston is the cause of combustion ' as meant to designate a real, actual, existent, we must pronounce this proposition false, not necessarily because the predicate fails to apply to the subject, but simply because the subject term fails to designate anything. Here the contradictory opposite gives no propblem : If it is false to say that phlogiston is the cause of combustion, it must be true to say that it is not the cause of combustion. And indeed it is true.
With ' phlogiston is the cause of combustion ' it seems that conceding the involvement of a null class does not cause any trouble. However, the subject term, although meant to designate something (real), does not designate anything. Therefore the statement is not about anything and so is not a proposition at all, and thus there is no susceptibility of truth or falsity.
Nevertheless we still want to say ' phlogiston is not the cause of combustion ', because that is an important result in chemistry.
If we now look to the proposition ' the present king of France is bald ', then here also we acknowledge that the proposition was meant to say something about something really and actually existing in extramental reality. But because there is no present king of France the subject term completely fails to designate, rendering the proposition false (if we disregard the fact that also here, because of failure of designation, there is no proposition at all). But, while the contradictory opposite of the proposition ' phlogiston is the cause of combustion ' was perfectly true, and thus causing no trouble, the contradictory opposite of ' the present king of France is bald ', which, consequently, is ' the present king of France is not bald ', cannot be true either (having thus a problem here), because unlike the case of phlogiston, being bald or not bald is totally accidental (with respect to 'king of France'). We cannot say : ' because there is no present king of France, he is not bald '. So the proposition ' the present king of France is not bald ' cannot be seen as true, because there is no present king of France. And because there is no present king of France this proposition is false, just like the proposition ' the present king of France is bald ', which is also false. So here we have the problem of contradictory opposites having the same truth value (still provided we, for the time being, ignore the fact that, because of failure of designation, it is not a proposition at all, and so does not involve possible truth values, that is, such a statement is neither true nor false.).
How must we solve these problems?
Considering again the proposition ' phlogiston is the cause of combustion ', how can we legitimately deny this proposition to be true, without finding out that it is not a proposition at all? That is to say, how do we manage to express in a genuine proposition -- namely by denying its truth -- an important result in chemistry?
To begin with, note once more that the reason for my insisting so strongly on the existential import of all propositions is that from the standpoint of an intentional Logic it is the precise nature and function of a proposition, in contrast to a mere concept, to intend things in their very acts of existing (whether potentially, actually, fictitionally, or whatnot). Accordingly, if a proposition is not about anything that is or exists in any sense, it just is not about anything at all, and is thus not a proposition.
Let us now, then, analyze carefully the precise nature of the designation or existential import that pertains to the two propositions ' phlogiston is the cause of combustion ' and ' phlogiston is not the cause of combustion '. The first one we want to deny, the second one we want to affirm.
We have said that we can deny the affirmative proposition on the ground that its subject term fails to designate anything. But yet, at the same time, by denying it we certainly understand something by the term ' phlogiston ', otherwise there was no proposition at all. But if we -- by conceding that something was understood by the term ' phlogiston ' -- say that this term happens to designate merely a being of reason, we run into trouble, because then we cannot unequivocally deny the proposition ' phlogiston is the cause of combustion ' anymore. It could well be true, for instance in the context of some fictitious chemistry.
To solve this problem we can do as follows :
In order to be able to deny that phlogiston is the cause of combustion, we must recognize on the one hand that phlogiston is no more than a being of reason -- an "inferred entity" with no basis in fact. And on the other hand, we must also recognize that in the proposition in question, viz., ' phologiston is the cause of combustion ', it is taken (by the proponent) as designating not a being of reason but a real being. Only by this kind of comparison or contrast is it possible to deny the proposition or to recognize it as being false. So now we can legitimately deny the affirmative proposition ' phlogiston is the cause of combustion ', because the proponent of it wrongly supposed that the term ' phlogiston ' designated something really and actually existing in extramental reality. And while we can now say that the proposition ' phlogiston is the cause of combustion ' is false -- not because of failing to designate anything, but because of failing to designate the right kind of being or existing (this right kind of being or existing would be that of a being of reason) -- we can now legitimately say that the negative proposition ' phlogiston is not the cause of combustion ' is true, because the non-existence (in extramental reality) of phlogiston, that is, its non-existence as such, implies that it is not the cause of combustion.
The conclusion to which all this points is that whenever an affirmative proposition is false because of a failure of designation on the part of its subject, this failure cannot be such that not anything is designated -- otherwise there would be no proposition -- but that there is a conflict between an intended (by the proponent) designation and the actual designation. And if the predicate is saying something essential with respect to the subject, as it is in ' phlogiston is the cause of combustion ' (to be the cause of combustion is the essence of phlogiston), then its contradictory opposite is true. In this way there is no problem with the truth value of the contradictory opposites.
We have now solved along the lines of intentional Logic the problem of the supposed null class for the case of the proposition ' phlogiston is the cause of combustion ' and its contradictory opposite. But how, in fact did we (following VEATCH ) solve it? We did it by showing that in this case there was no null class at all : The actual designation turned out to be a being of reason (while the intended designation was a real being). The proponent meant a real being, but it turned out to be a mere imaginary being, and therefore the proposition ' phlogiston is the cause of combustion ' is false. Or, said differently, the conflict between intended and actual designation rendered the proposition false.
Now we will turn to the proposition ' the present king of France is bald ', which also is supposed to involve the null class.
To begin with, this proposition differs from the first proposition (phlogiston) in two important ways :
Let us now proceed to analyze this proposition ' the present king of France is bald ', and its contradictory opposite ' the present king of France is not bald ', as to their truth or falsity and their proper designation.
Let us now return to the proposition
all the dimes in my pocket are shiny.
Here we have the same case of a 'definite description' pinning down the designation (but here the transition from the affirmative proposition to the contradictory opposite involves a change in quantity, a change that is, from 'all' to 'some'). The subject term not only is meant to designate, but also actually designates the dimes in my pocket. So also here, like in the case of the present king of France, the failure of designation is complete when there are no dimes in my pocket. And because, like in the present king of France, the predicate ( ' shiny ' ) does not express something essential to the subject, the failure of designation of the affirmative proposition (A), rendering it false, does not have the contrary proposition (E) ' no dimes in my pocket are shiny ', which is equivalent to ' all the dimes in my pocket are not shiny ', true-as-a-result-of the non-existence of dimes in my pocket, because presence or absence of dimes in my pocket does not have any bearing on their being shiny or not shiny. If all dimes in the world were necessarily shiny, and if there could be no shiny things other than dimes, then, indeed, the absence of dimes implies the absence of being shiny. In fact, however, being shiny is accidental to dimes, and there are other things besides dimes that can be shiny. If I have dimes in my pocket, some of them could be shiny, some could be mat. And because there are no dimes in my pocket the E proposition fails, like the A proposition, to designate, and therefore is, like the A proposition, false. This, however, does not violate the law of contraries.
But if we move to the corresponding O proposition ' some dimes in my pocket are not shiny ', then, even for the mathematical logicians, but also for the intentional logicians, the proposition is -- when considered a proposition at all -- false (if there are no dimes in my pocket, as assumed), because the subject term, which is meant to designate actual existents, fails to designate. So this O proposition, like the A proposition, is false, implying corresponding contradictory opposites having the same truth value, and thus violating the rule with respect to these opposites.
Only when we remove the definite description, namely by propounding ' any dime in my pocket is shiny ', we have no problem, because, here, obviously, even if there are no dimes in my pocket, or even if there never have been, the proposition still does not fail to designate, because all that is called for is a designation of possible existents and not necessarily of actual ones. So here there turns out not to be a null class. The problem is thus solved with respect to the proposition ' any dime in my pocket is shiny ', while in the case of ' all the dimes in my pocket are shiny ' the problem is also solved, still in the context of an intentional Logic, but now on the basis of the insight that this is no proposition at all and thus is neither true nor false. And this means that to solve this last problem we did not have to deny existential import to A propositions, meaning that we stay in line with the tenets of intentional Logic.
And let us now return to the proposition
all sea serpents live in the Atlantic,
where supposedly a null class is involved (because sea serpents do not exist, and have never existed in extramental reality). Here we have a case where we do not have to do with a 'definite description'. That is, the designation of the subject term is not beforehand completely fixed by the proposition or by elements of it. Further, in this case, there is no necessary connection between subject and predicate : The existence or non-existence of sea serpents does not decide whether they live in the Atlantic or not. So although the proposition ' all sea serpents live in the Atlantic ' is comparable with the proposition ' phlogiston is the cause of combustion ' because of the fact that in both cases the designation is not totally fixed (both can be about mere beings of reason), they differ in the fact that in the case of ' phlogiston is the cause of combustion ' the corresponding negative proposition is true because of the non-existence in extramental reality of phlogiston, while in the case of the sea serpents the corresponding negative proposition is not rendered true by such a non-existence of sea serpents (existence or non-existence of sea serpents does not decide whether they, or some of them, live in the Atlantic or not). In contrast to the proposition about phlogiston, the affirmative proposition about sea serpents has two negatives, viz., its contrary : ' all sea serpents do not live in the Atlantic ' and its contradictory opposite : ' some sea serpents do not live in the Atlantic '. And indeed their non-existence doesn't make all of them or some of them not living in the Atlantic.
Of course it is a fact that when there are no sea serpents at all in extramental reality, they also do not live in the Atlantic (like, when there isn't a present king of France, he is obviously not bald). But the case of phlogiston is different : Being the cause of combustion is wholly essential to what phlogiston is (or was meant to be), so the non-existence of phlogiston in the sense that there is no place for it in the chemical world, is equivalent to its not being the cause of combustion.
On the other hand, living in the Atlantic, instead of in other oceans, is not essential to what sea serpents are (or what they were meant to be), so their non-existence has nothing to do with the Atlantic Ocean as contrasted with other oceans. If sea serpents do not exist at all, they do not live in any ocean.
So the proposition ' all sea serpents live in the Atlantic ' is false because of the discrepancy of meant and actual designation of the subject term. The negative proposition (here the contradictory opposite) ' some sea serpents do not live in the Atlantic ' then must be true, and is in fact true. Let us explain.
In both the affirmative and the negative proposition the meant designation was the same (otherwise they would not be comparable with respect to truth values), namely real sea serpents, but because the actual designation is only of beings of reason, the affirmative proposition is false. In the negative proposition the meant designation was -- as has been said -- also of real sea serpents, but the actual designation is also of real sea serpents, because here the proposition is indeed about real sea serpents not living in the Atlantic Ocean, so here there is no discrepancy between meant and actual designation. And it is true that real sea serpents, and thus also some real sea serpents, do not live in the Atlantic. So here we have no problem with the truth values of contradictory opposites.
As for the corresponding contrary proposition (E), ' no sea serpents live in the Atlantic ' must be true. Also here the meant designation is of real sea serpents, and the actual designation is also of real sea serpents. The proposition says of these that they do not live in the Atlantic, which is obviously true if there are no sea serpents at all. So here the A proposition is false and the corresponding E proposition is true, and thus there is no problem with the truth values of contraries.
Accordingly, it would seem to be only in the case of definite descriptions (present king of France, the dimes in my pocket) that a proposition can fail so completely in designation as to be utterly without existential import. Yet, when this occurs, the proposition simply ceases to be a proposition. Indeed, have we not already observed how this happens in the case of the liar paradox (Logic, Part III), and do we not now have further confirmation of the fact as a result of these current investigations?
In conclusion, may we not say that so far as the null class is concerned, it really does not pose any problem so far as the existential import of propositions is concerned? For a subject term involving the so-called null class is either so used as not to exclude designation altogether, and hence remaining to have existential import, which is equivalent to there being no null class, or when, as in the case of definite descriptions, it is so used as to exclude all designation, and thus conceding that we have to do with a genuine null class, then one immediately recognizes that one's proposition is not a proposition about anything, and hence not even a proposition.
Let us hope (so VEATCH, rightly concludes, p.263) that these considerations may serve to exorcize from Logic, for good and all, that plaguing devil of the null class.
This concludes our exposition of the theory of designation (supposition, suppositio), and its testing on the problem of the null class.
At the same time we have also come to an end of our exposition of the PROPOSITION.
In the next document we will turn our attention to the last of the three major divisions of intentional Logic, viz., the structure and function of ARGUMENT in Logic.
e-mail :

To continue click HERE for further study of Logic, Part VI.
Back to Aristotelian metaphysics Part I
Back to Aristotelian metaphysics Part II
Back to Aristotelian metaphysics Part III
Back to Aristotelian metaphysics Part IIIa
Back to Aristotelian metaphysics Part IV
Back to Aristotelian metaphysics Part V