e-mail : 

Back to Homepage

To know something is at least knowing (completely or still incompletely) the what of a thing. This is what is intended by the concept. And although a genuine logic presupposes metaphysics, that is, presupposes things, because they are the entities to the knowledge of which Logic is geared, we should be aware that the what, which is intended by a concept, is not a pre-established type of what :  It is the what of anything whatsoever (of substances, accidents, aggregates). So when we, in the present context, call such a what 'essence', or 'nature', it is not a special type of nature that is meant, for example the essence of a substance, but just the nature or essence, or content of whatever entity. So while it is the business of a concept to intend an essence, it is not within its competence to make completely and fully explicit the distinction between what is essential and what is merely accidental. When we would assume it had this competence, we would load onto the concept a function that properly pertains to the proposition. A simple apprehension of an essence in and through a concept, is necessarily preliminary to any further understanding of that essence in and through propositions (VEATCH, p.84).
Because a concept is initially abstracted from sense experience ( NOTE 26 ),  it is perfectly well-adapted to a re-application to (entities of) sensory experience.
The Given, although it be given to the senses, does not itself consist merely of sense qualia, nor is it exhaustively cognized merely through sensory apprehension. The real thing, or being, itself, and that real thing in toto, is given or presented to our sense faculties (where each faculty has its own proper and specific object, like sound for hearing, and color for vision). But these faculties alone are unable to grasp such a presented being adequately or even to apprehend what is most essential to it (if the being be a substance for example). So more is given to the senses, than they themselves can apprehend. Or, in other words, more is given to the senses than just their proper specific object. The senses are the bearer of a message which they themselves are incapable of (completely) reading and which only the intellect (which processes [sensory] data) can decipher (completely). So the presence of fully-fledged  s u b s t a n c e  cannot be (fully) apprehended by the senses (they only apprehend colors, tones, figures, etc.), but is nevertheless  g i v e n  or  p r e s e n t e d  to the senses in sensory experience :  While actually existing substances (in the metaphysical sense) are not 'properly sensible' (sensibile  per se), that is, are not the proper object of any sense faculty, in the way in which colors and pressures are, they are nevertheless 'accidentally sensible' (sensibile  per accidens). The reason is that it is  the very same thing or being  that is presented to sense (and whose properly sensible qualities are apprehended by the senses), that comes to be recognized by the intellect as existing substantially in itself (that is, ontologically independently) and not as a mere accident of something else. In other words, there is no question here of  "inferred entities",  if one means by that an inference from an entity that is given,  to  one that is not given at all. It is the whole existing substance that is given in the first place (this is something that we directly experience) and not a mere set of sense qualia.
And of course we can be mistaken as to what is given in a particular sense experience, but this can always be amended by another sense experience (the sound I heard turned out not to have come from a passing car, but from the neighbors).
We are able to form a concept of a (type of) thing by repeatedly sensing qualities and other determinations (such as sizes and shapes), because the thing as thing is also (i.e. in addition to qualities, etc.) given despite the fact that we can make errors as to what (thing) these qualities, etc. belong. The thing is concurrently given, but must still be extracted as such from the Given. And this is the whole process of developing a concept of one or another (type of) thing.
Why, suppose, as many philosophers do, that with the sense data, and also with the subsequent verifying sense data, no more is given than these bare sense qualia themselves? Much more is given than can be apprehended by the senses just as such. Denying this is the result of the wish to find simple, absolute, and indubitable starting points for knowledge, out of which all other knowledge must somehow be built up or logically constructed. Why suppose that what is given in experience must be bare, simple, and indubitable? Why not suppose it to be rich, complex, and very easily misunderstood?
So when one says that substance (as carrier of accidents) is just an inferred and superfluous idea is just begging the question, because one had already presupposed that all that is given are only bare sense data.
The evidence that  things  (and not only bare sense data) are given in sensory experience follows directly from more fundamental presuppositions, and these latter are no less than the assumption of a realistic theory of knowledge :  If not the whole thing would be given in sense experience (but not necessarily directly apprehended on first occasion of such a sense experience), then we had, in order to arrive at the whole thing, to add data of quite another nature, that is, we have to mentally construct (i.e., not re-construct, but partially create) these whole things, which means that we bring in a subjective element into our knowledge. And this is totally contrary to the acceptance of a realistic view of knowledge. So things are given in sensory experience. And what in that experience cannot be directly apprehended by the senses themselves, will be apprehended by the intellect by processing these data. In this way concepts are (gradually) formed. Now we can say, that the intellect apprehends that the qualities, etc., which are as such apprehended by the senses, belong to a substance (which latter was given, but not as such apprehended by the senses). If we generalize the acquired concepts we arrive at the Category of Substance, while understanding that the qualities as such are not things but affections of things. In this way we arrive at the several possible fundamental types of descriptions of a thing, namely either as it is in itself, or as it is affected in some way. Seen in this way, the Aristotelian Categories are ways signification  of  a same given thing. This is done in the moderate nominalism of Ockham. As such Aristotle's booklet of Categories is a logical treatise.
On the other hand, if we view qualities, etc. as  beings  of some sort, then the scheme of Aristotelian Categories is a classification of ways of being. Then Aristotle's booklet is a metaphysical treatise. This is advocated by Classical Substance-Accident Metaphysics.
Perhaps the difference between these two positions is not so big and significant as it looks :  After all, the qualities etc. by which a thing can be described must at least co-exist with that thing, because these qualities are objective, they are not mental constructions or creations.
Indeed, Ockham's criticisms against substance and accident are not straightly directed against St Thomas (who is the very representative of the Classical Substance-Accident metaphysics), but against Duns Scotus, who viewed accidents as genuine things, on a par, in a way, with substance. Accidents can, it is true, perhaps be known or conceived apart from substance, but they cannot be apart from substance.

Given a group of objects, we sometimes wish to speak of a common property of all these objects. We then abstract this property from its concrete expression in the varius objects, i.e. we disregard the differences between the objects and select the common property as the focus of our attention. The term "abstraction" has here the meaning "separation from". Thus the property of redness can be defined by abstracting it from a group of red objects.
Russell has shown that this psychological analysis of the process can be replaced by a purely logical procedure. First, we must define the group of objects from which the abstraction is to be made. We then find that all these objects are connected by a symmetrical relation :  in our example, the relation of color-similarity. Starting from a particular object, say a certain rose, we thus can define the class of objects having this relation to the selected object, for instance, the class of objects which are color-similar to this rose. Instead of speaking of the common property we then simply speak of the class so defined. In other words, instead of saying that an object is red, we shall say that an object is a member of the class of things color-similar to this rose.
This logical version of the process of abstraction shows clearly that it represents an ostensive definition of a property, i.e. a definition given by the act of pointing to a physical object. But it shows also that we need not regard the property as something removable from the concrete object. Instead of imagining a separation between property and object we rather regard the property as given by a union of objects. The notion of property thus can be replaced by the notion of class. The abstraction of the common feature of the group of objects is replaced by the transition to the totality of the group.

To do away with abstract properties and [thus with] concepts, and then, necessarily, also with natures and essences, is a form of nominalism. It concentrates on individuals and classes of individuals. Thereby we must remain to be aware that the nominalism of Ockham, who is for us the most important representative of this line of thought, is very moderate, because, for instance, he still accepts the existence of some sort of Essence in things, evident from the fact that he excludes contingent circumstances when outlining the signification of genera and species  ( MOODY, E., The Logic of William of Ockham, 1965, p.98/9 ).  This means that what is left, when these circumstances are (mentally) removed, is the carrier-only, or, equivalently, the historical individual, and this is the genotypic + phenotypic  essence  of the thing.

Classes, although, from the view of intentional logic, not being logical entities, do play an important part in determining the supposition or designation of a concept when it is part of a proposition. We will treat extensively of this important theme later when dealing with propositions. For the time being, though, we can expound it as follows :
Universal concepts (such as, for instance, 'man'), which are relations of identity between an abstracted essence and the particulars from which it has been abstracted, that is, from the individuals of the concept's extension, enter into further relations of identity with each other in propositions. As a consequence of these further relations it becomes necessary to determine what portion of the extension of a given concept is of concern in the context of a given proposition or argument.
That classes are not logical entities is not because they are real (instead of mental) entities, because they are not. They are not logical entities because they are non-intentional entities.
It is all right to insist that in reality there are only individuals (as nominalism says) and that these individuals are really similar to one another in various ways. But still this leaves open the question of how, and through what logical tools and devices these classes of similar individuals may be intended or known. Nor would there seem to be any other way of so knowing or intending a class of individuals save by abstracting what these individuals are and then recognizing that the abstracted essence is related by a relation of identity to the individual members of the class:  It is only because an object is really red itself that it can be color-similar to this rose. Nor if this rose, in turn, were not itself really red, no other red object could be really color-similar to it  ( VEATCH, p.120).
So class membership is consequent upon recognizing the abstracted essence, meaning that we cannot do away with abstraction. Thus a concept, being but a relation of identity between an abstracted nature or essence and (the individuals of) its extension, is simply an intention of a class of individuals. The class, on the otherhand, is not an intention at all (because in order to use it as a sign it must first itself be known, but then it is no more than just an instrumental sign) but rather what is intended. That a class is not an intentional entity is (also) clear from how it is formed :  From the set of all individuals whatsoever one selects those individuals that can be related in a certain respect to some single individual that is pointed to. And so a subset is formed, which is called a class. So a class is consciously formed by the investigating mind and is then as such known. As long as it is not explicitly known we cannot use it as a sign, and so, again, if the class is a sign, it is just an instumental sign and thus not an intentional sign (which needs not first to be explicitly known before it can be used as a sign).
So to substitute concepts, which are intentional entities, for classes, which are non-intentional entities, is to dispose of the very core feature of Logic, namely intentionality, that is, sacrificing intentionality for formalism and to replace the properly logical relations of identity with the non-intentional relations of mathematics -- in this case, the conceptual and subject-predicate relations of identity with relations of class inclusion and class membership, which belong to set theory which is a mathematical discipline.

Indeed, I myself am inclined to assert that  " mathematical Logic "  is just a part of mathematics, like Group Theory, and Set Theory, for instance are, or perhaps of meta-mathematics (that is, mathematics about mathematics). This part characterizes itself by, firstly, being very general indeed, and, secondly, by treating of a special mathematical function, which is called the 'truth function', because it shows a certain analogy with the truth function in genuine Logic (that is, intentional Logic) insofar as this Logic is about knowing extramental real beings, a Logic that is, where truth is dependent on the significata, as they exist in extramental reality, of the terms in a proposition.
As regards mathematical objects, which can legitmately considered to be objective, meaning that they are what they are, independently of their being known, they also can be the objects of logical intentions, that is, they can be intended by logical entities as to what they are. I suppose that the truth function here will be a bit different, because of the immaterial nature of mathematical objects. It is probably the truth function as used in mathematical Logic (endorsed with quirks as was discovered by GÖDEL and TARSKI ).
For the intentional Logic concerning the knowledge of extramental real beings a metaphysical truth function is involved. All this is, however, in need of further enquiry.

x  --->  f(x)

in turn meaning that x is associated with f(x).
Indeed, such a propositional function expresses the relational character of a concept :  Socrates (x) is a human being (f), or, Socrates (x) is sad (f).
As we have intimated earlier, a concept implicitly implies such relations, that is, relations of identity between the things and the formal content abstracted from them. However, many mathematical logicians do not limit labeling something as  ' propositional function '  to such a relation of identity, which is the concept, but extent it to include relations connecting two or more relata. All these are called  ' propositional functions '  or universals.
To investigate the legitimacy of this (extension) within the context of an intentional Logic, let us consider two examples of propositional functions (given by a mathematical logician and quoted in VEATCH, p.132) :

Cassio is sad   F(x)   (one-place propositional function)

Cassio loves Desdemona   F(x,y)   (two-place propositional function)

As for  ' Cassio is sad ',  the concept  ' sad '  is related to its subject term by a relation of identity ( NOTE 28 ).  And this identity is expressed by the copula  ' is '.
On the other hand, we cannot say this with respect to  ' Cassio loves Desdemona ' :  While in  ' Cassio is sad '  the function is predicated of Cassio (that is, the function term is predicated of the term  ' Cassio ' )  (and there the function was :  sad ),  it is not so in  ' Cassio loves Desdemona '  :  We cannot say :  ' Cassio is loves Desdemona ',  and, more generally (we cannot say) :  ' Cassio is loves '.
The function can also not be predicated of the term  ' Desdemona ',  for we cannot say :  ' Desdemona is loves '.
Of course when we reformulate the proposition  ' Cassio loves Desdemona '  (which is an instance of the two-place function  ' loves ' )  as  ' Cassio is a lover of Desdemona '  (which is an instance of the one-place function  ' lover of Desdemona ' )  we obtain a genuine relation of identity :  ' Cassio [subject] is [copula] a lover of Desdemona [predicate] '.  So in order to obtain genuine relations of identity, we must convert all many-place propositional functions into one-place propositional functions. And because many mathematical logicians do not do this, they confuse intentional and non-intentional propositional functions, because all the many-place propositional functions are non-intentional. This, again, because the many-place function cannot be predicated of its subjects (We cannot say :  ' Cassio is loves ',  nor  ' Desdemona is loves ' ),  and only predicability gives us the relation of identity, and only a relation of identity is truly intentional, because it separates and re-unites again, which is the very act of intention, resulting in our knowing the what of things.
The relation between  ' sad '  and  ' Cassio '  does not correspond to a real relation (because Cassio is not identical to sad ),  also not in the context of classes because classes are themselves not real (but beings of reason) while the individuals included in these classes are. The relation is just a logical intention.
On the other hand, the relation between  ' loves '  and  ' Cassio '  corresponds to a real relation, because Cassio really loves (someone). So this relation, because it is real, cannot be a logical intention. It only becomes one if we convert it to :  ' Cassio is a lover ',  and then, like in  ' Cassio is sad ',  a state of Cassio is intended, and thus known.
Also the real relation between Cassio and Desdemona, namely the relation  loves,  in no way represents or intends what Cassio is (only what Cassio does, but this is not a relation of identity), or Desdemona, or anything else for that matter.

To be sure, either of these relations (viz., the relation between  ' loves '  and  ' Cassio '  [or between  ' loves Dedemona '  and  ' Cassio '  for that matter]  and  the relation between Cassio and Desdemona, namely  loves )  may be made the object of an intention, but neither can themselves be an intention, because  ' Cassio loves (Desdemona) '  is  not a subject-predicate relation (while  ' Cassio is sad '  is  a subject-predicate relation). Instead, no sooner is such a relation made the object of an intention, than the intention itself turns out to be nothing other than a relation of identity.
For instance, if one wishes to consider the relation of Cassio to Desdemona, and to state what that relation is, one will say that it is a relation of lover to loved, or that it is asymmetrical, or that it is a predicamental relation, etc. In other words, the minute the relation of Cassio to Desdemona becomes the object of a concept, or the subject of a proposition, ( NOTE 29 )  then

(1) the relation of the universal concept to that particular relation,

namely  ... loves ... [ = universal concept]  to  Cassio loves Desdemona [ = the particular relation], as expressed in :

Cassio loves Desdemona  [subject]  is  [copula]  an instance of :  ... loves ...  [predicate], 

or,

(2) the relation of the predicate (expressing a property) of the proposition  to  that relation (figuring) as the subject of that same proposition  ---

Cassio loves Desdemona [subject]  is  [copula]  asymmetrical [predicate]  ---

is a relation of identity, that is to say, it manifests what that relation is  ( VEATCH, p.135 ).

The same goes for the relation between  Cassio  and  loves  (or  Cassio  and  loves Desdemona ).  Also this relation is, as has been said, a real relation, namely between Cassio and a state in which he is in ( NOTE 30 ).  When we make this relation the object of an intention, and thus the object of a concept, or the subject of a proposition, then

(1) the relation of the universal concept (substance--state) to that particular relation (Cassio--loves), which can be expressed as :

The relation between Cassio and loves [subject]  is [copula] an instance of the general relation between substance and state [predicate],

or,

(2) the relation of the predicate (expressing a property) of the proposition to that relation as subject, as in :

The relation between Cassio and loves [subject]  is  [copula] a transcendental relation [predicate],

is a relation of identity, that is to say, it manifests what that relation is.

By treating one-place functions on a par with many-place functions, the mathematical logicians have treated genuine intentional relations in the same way as they had treated non-intentional relations. Accordingly, with propositional functions we can witness the same thing happening that happened with classes.

The  paradoxes  have forced mathematicians and mathematical logicians to review much in these disciplines, and are brought up as a critique against Aristotelian Logic (and consequently also against an intentional Logic as devised by VEATCH and worked over by me).
First of all we will restrict ourselves, of course, to the genuinely logical paradoxes. The principal outcome of the mathematical logician's recognition of these paradoxes is their insistence that Logic is not to be regarded as one and simple, but rather as involving a hierarchy of types or a multiplicity of Logics and Metalogics (VEATCH, p.139). I add to this that the sequence of metalogics will not, as might perhaps be expected, run off into infinity, because this sequence eventually ends up, or bounces into, the hardware of the brain, and the latter does not work according to  rules,  but according to (natural)  laws,  that is, according to causal necessity. And for this necessity no rules are necessary (See HOFSTADTER, D., Gödel, Escher, Bach, 20th-anniversary edition, 2000, p.170, Section The "Jukebox" Theory of Meaning, and the next Section Against the Jukebox Theory ).

Among the logical paradoxes we have two types :  conceptual paradoxes and propositional paradoxes.
To the former belong that of  the class of nonself-membered classes, and the paradox of the "impredicable". To the latter the liar paradox.
Following VEATCH, pp.140, we will start with the  conceptual paradoxes.
For this, it suffices to treat of just one of them (as representing them all), namely the  paradox of the "impredicable". Let us systematically expound this paradox.

As a preliminary we might note the following :
The term (not in the linguistic sense, that is, not the word )  ' red '  is a term of first intention. It intends a certain well-defined state of some substances in extramental reality.
The term  ' concept of red ',  on the other hand, is a term of second intention. It intends the first intention  ' red ',  that is, it intends the term  ' red '  taken in first intention. Or, equivalently, it is the term  ' red '  taken in second intention.

All terms can be predicated of themselves. For instance in  ' red is red ' .
Many terms, however, cannot be applied to their objects when taken in second intention :  We cannot say :  ' the concept of red  is  red '.  Such terms or predicates we call "impredicable" ( NOTE 30a ).
On the other hand, while, as has been said, all terms can be predicated of themselves, there are a number of terms among them that also apply to their objects when taken in second intention :  For instance, while we can, of course, say, with respect to the analogous concept  ' being '  :  ' a being is a being ',  we can also legitimately say :  ' the concept of a being is a being '  (it is namely a being of reason). Such terms or predicates we call "predicable".
And of course it seems that any term or predicate is either "impredicable" or "predicable".
It is here, however, that the paradox appears :

Indeed, if we now ask whether the term "impredicable" ( NOTE 31 )  itself is "predicable" or "impredicable", we run into a paradox, because both alternatives give contradiction :

If we suppose that the term "impredicable" is "impredicable" (first alternative), then we must admit that precisely because of this (assumed) fact it is "predicable" ( NOTE 32 ).
So we have a contradiction.

If, on the other hand, we suppose that the term "impredicable" is "predicable" (second alternative), then we must admit that it must be "impredicable".
So again a contradiction.

And because both alternatives (while there being no more of them) lead to contradiction, we have a paradox ( NOTE 33 ).

While asking about the term "impredicable" led to paradox, asking about the term "predicable" does not. Let us see the alternatives :

First alternative :  while in all cases we can say  ' predicable is predicable ',  we also say :

the term or concept of "predicable" is "predicable".

And indeed  if  it is predicable, then it must be predicable. No contradiction is apparently involved.

Second alternative :  while in all cases we can say  ' predicable is predicable ',  we also might say :

the term or concept of "predicable" is "impredicable".

If  this is true, then we cannot say :

the term or concept of "predicable" is (itself) "predicable",

but should say :

the term or concept of "predicable" is "impredicable",

that is, the term "predicable" taken in second intention is "impredicable", while taken in first intention it is "predicable".
And this could be the case, just like we could not say :

the term or concept of  ' red '  is red.

So also here no contradiction is apparently involved.

And further investigation will reveal one of these alternatives to be true (See further down ).

VEATCH, p.141, says about all this the following :

The mathematical logicians, in the face of this paradox, have proposed a cure which, it would seem to me, would really kill the patient. They propose that since the idea of "impredicable" concepts, or of nonself-membered classes leads to paradox, the thing to do is to rule out the notions of "predicable" concepts and of self-membered classes. This is done either by a theory of types or by a theory of metalanguages. [...] They both establisn by decree the illegitimacy of all notions or concepts which would seem to apply to their proper objects, not only when these are taken in first intention, but also when they are taken in second intention.

Indeed, when concepts are considered to be  sets  of individual entities, we arrive at a paradox when considering self-membered sets :
If we say that the concept of  "impredicable" concepts  is  the set of all "impredicable" concepts, and the concept of  "predicable" concepts  is  the set of all "predicable" concepts, then we can ask :

Is the set of all "impredicable" concepts itself a member of the set of all "impredicable" concepts, or is it a member of the set of all "predicable" concepts ?

The first alternative amounts to the supposition that a set can (in certain cases) be a member of itself, which is flatly absurd :  A whole can never be a part of itself (certainly insofar we speak about finite wholes). So it seems legitimate to rule out self-membered sets, which here means that we should rule out that the concept of the "impredicable" is itself "impredicable" (note that in this line of reasoning we have just switched from set membership to belonging to a concept). So the concept of the "impredicable" must be "predicable", but then, again, the concept of the "impredicable" must be "impredicable", which, however, was ruled out. So we must abandon the whole question as to whether the concept of the "impredicable" is "impredicable" or "predicable". The question is thus, according to the mathematical logicians, meaningless.
But such a solution of the paradox is unacceptable for an intentional Logic, because for it it is very natural to conceive of a logical intention, which, in intending its object, would intend itself as well -- or better, which would be such as to intend its object considered in second intention, quite as much as in first intention (the term  ' the term "red" '  intends the form  red  in second intention, while the term  ' red '  intends the form  red  in first intention). So the term "impredicable" intends "impredicable" concepts (either the one , or the other). But also this term itself must be such as allowing it to be intended. This we do by the term  ' the term "impredicable" '  (one or another "impredicable" concept is intended as second intention). And we can then ask whether this term is "predicable" or "impredicable", that is we can ask whether the term  ' the term "impredicable" '  is "predicable" or "impredicable", and this is, of course, a legitimate question. Thus, if I say :  the term "impredicable" is (itself) "impredicable", that is, if I do not interpret this purely extensively (in the exclusively quantitative sense), then I would not have a case that the set of all "impredicable" concepts is a member of the set of all "impredicable" concepts.
It would seem that the conclusion to be drawn (as already hinted at) from this situation would be not that  classes,  representing concepts, must be ruled out as soon as they turn out to be self-membered classes, but that only  sets  (in the mathematical sense) that are self-membered must be ruled out.
This can only be consistent if we differentiate between (1) classes-not-as-mathematical-sets (that is, not as purely quantitative collections) but classes somehow interpreted as logical entities (which are itentional), and (2) purely quantitative mathematical sets (which are not intentional).
Just as these (viz., logical classes, [versus] mathematical classes) are radically different from each other (the one being intentional, the other non-intentional), implying that ruling out the one does not necessarily entail the ruling out of the other, we also should not rule out  concepts  that turn out to be "predicable" (for example the concept of a being is a being), because concepts are radically different from mathematical quantitative sets (again, because concepts are intentional, while mathematical sets are not).
While it would seem difficult and even impossible to conceive of a whole (at the same time) being a part of itself, it is not only not difficult but even very natural to conceive of a logical intention, which, in intending its object, would intend itself as well.

But, elsewhere we have said that the essence of a formal sign (a logical intention) lies solely in the fact that it signifies something else, that is, something other than itself. The conclusion seems to be that a logical intention cannot intend itself. However, when we have the case of an intention of an intention, we do not have an intention that intends itself, as the next diagram illustrates :

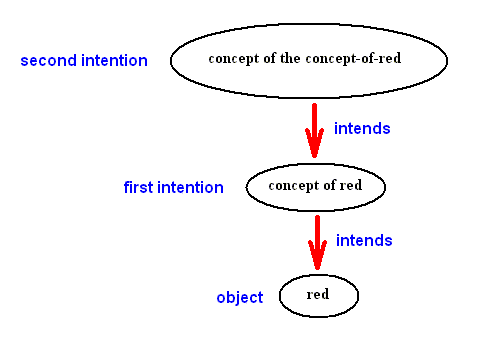
Here we see that a second intention refers to a first intention (and a first intention to an object). So here there is no complete self-reference (and it appears evident that only complete self-reference can generate a paradox). The concept of red intends red. It can, however, also intend itself (the intention now intends itself, that is, bends onto itself), but it must do this by means of a second intention, so again, the self-reference is not total.

Moreover, not only do such "predicable" concepts and self-membered logical classes seem perfectly natural and normal from an intentional point of view, but in addition they are absolutely indispensable. Without such concepts the very analogy of Being itself (in the sense of :  being can come in several distinct types such as substance, accidents, beings of reason, etc.) could not be recognized, since it is only in an analogous [equivocal] concept that such analogy (of being itself) can be apprehended, and an analogous concept of the sort here required is indeed a "predicable" concept  ( VEATCH, p.142 ).

The solution of the paradox in terms of a multiplicity of Logics, or (logical) languages, or sets of rules ( NOTE 34 ),  is also because of another reason unacceptable, because it destroys the unity of Logic. That is, without "predicable" concepts there is not one single Logic anymore, but a multiplicity of logics and metalogics.
Nor is that all, for even to propound such a theory to the effect that logical entities are not univocal but systematically ambiguous ( NOTE 35 ) -- even to enunciate such a principle would seem to violate the very principle enunciated. For the principle itself is certainly about all logical entities, namely that they do not form a unity but are distributed over several different logical systems, different logics. So this principle itself belongs to the one Logic after all !
The proposition  ' not any logical proposition is about all logical propositions '  leads to contradiction (because this is about all logical propositions). Therefore there must exist at least one logical proposition that is about all logical propositions, which implies that we nevertheless have something like one Logic. But such a proposition, which is about all logical propositions, is then also about itself, which means that this kind of self-reference must be admitted. And this is possible because here we have not a case of complete or total self-reference.

To introduce this new line of approach (which will later be supplemented by additional ideas), let me quote VEATCH, p.142--144 [comments in square brackets] :

Supposing that not only do certain "predicable" concepts seem natural and normal but also that their elimination seems to involve serious inconvenience and even downright contradiction, then one wonders whether the solution to the paradoxes had not better be sought along some other lines than the total elimination of all "predicable" concepts and self-membered classes. As to what such an other line might be, the one which most naturally suggests itself is that of showing that the paradoxes are nothing but sophisms, and that, so far from requiring a radical revision of the whole theory of logic, they really demand nothing but a more determined use of the already recognized principles of logical analysis.
Can the paradoxes be shown to be mere sophisms? I should like to think that they could, but I have no great confidence that I have actually succeeded in doing it. Nevertheless, as a step in this direction I think it might be illuminating if some sort of classification could be given of the types of concept that are susceptible of this strange "predicability", or of classes that are capable of this so-called self-membership. So far as I know, this has never been very seriously attempted. Instead, logicians have seemed content with citing only random examples of such concepts and classes.
As a first group of such "predicable" concepts, there might be mentioned the so-called analogous or transcendental concepts -- concepts such as "being", "thing", "one", etc. Indeed, we have already considered some illustrations of how concepts such as these must be regarded as being "predicable". Thus, the concept of "being", for instance, quite obviously applies not only to any being taken in first intention but also to the concept itself of that being -- i.e., to that same being considered in second intention.
As a second type of such "predicable" concepts might be reckoned various concepts of second intentional or logical entities. For instance, a concept of a concept is itself a concept, or a proposition about a proposition is itself a proposition [So an entity, here an intention of an intention, intending a proposition can itself also be a proposition (it can also -- in some cases -- not be a proposition, but a concept)], or an argument designed to demonstrate something about an argument is itself an argument. To be sure, there is an obvious limitation that must be placed on the "predicability" of such concepts. Thus, although the concept of a concept is itself a concept, the concept of a proposition is certainly not a proposition. Despite such limitations, "predicability" would certainly seem to be a fact about any number of intentions of intentions.
Finally, as a third class of "predicable" concepts, one might consider negative or, in the more old-fashioned terminology, infinite concepts -- i.e., concepts like the nonred, the noninflammable, etc. Thus the concept of the noninflammable is itself noninflammable, etc. But once again there is an interesting limitation on the "predicability" of these negative concepts. Obviously, if the negative concept represents a negation of any of the conceptual or second-intentional characteristics that pertain to the concept itself of such a negative notion, then that notion will not be "predicable". The concept of the nonconceptual is not itself nonconceptual. Or the concept of the nonlogical or extralogical is not nonlogical. Or the concept of the nonabstract is not itself nonabstract.
Given such a classification of the types of concept that are "predicable", it becomes obvious that the range of incidence of the paradoxes is very restricted indeed. There is nothing paradoxical about the "predicability" of analogous concepts and nothing paradoxical about the "predicability" of logical or second intentional concepts. Paradoxes arise only in the case of negative concepts, e.g., the concept of the  non-"predicable"  or  the  "impredicable",  or the class  of  nonself-membered classes.
Nor, obviously, do all such negative concepts give rise to paradox, but only certain ones. And more specifically, those certain ones would appear to be such negative concepts as involve the negation of the very character of "predicability" or self-memberedness. [...]
As I see it, the possibility of thus pinpointing the area in which the paradoxes arise is not without significance, for it tends to confirm my thesis that the trouble lies not with "predicability" or self-memberedness as such. On the contrary, these features of certain concepts would seem both undeniable and indispensable. It is only in a certain special connection and only in the case of a particular kind of concept that any paradox arises in connection with "predicability". Accordingly, the more natural procedure would appear to be not to rule out "predicability" as such and a priori, and as being somehow dubious per se, but rather to examine more carefully the particular circumstances in which "predicability" apparently lead to paradox. Perhaps we can here discover certain latent sources of misunderstanding and confusion which will account for this seeming paradox of "predicability", whenhever these particular circumstances are present.
As a matter of fact, I venture to suggest that once such an investigation is pushed with determination the paradoxes will in each case begin increasingly to look as if they were more apparent than real. Of course, at this juncture, such a suggestion must appear altogether incredible.

The paradox of the "impredicable" is so peculiar that the contradictions of both alternatives, and hence the paradox, is only an apparent one. More specifically, we could wonder whether when one says that the concept of the "impredicable" is "predicable" simply in virtue of its being not "predicable" -- whether one does not mean the latter in a somewhat different sense from the former (and so also that the concept of the "impredicable" is "impredicable" simply in virtue of its being "predicable").
Let us examine this more closely.
The starting point, let us say, is the initial supposition (the first possible alternative) that the concept of the "impredicable" is itself "impredicable". Now by this we mean that the concept of the "impredicable" is just not a "predicable" concept. That is to say, it is not (according to this first possible alternative) the kind of concept that applies both to its objects taken in first intention, and to itself, that is, to its objects in second intention (just like the fact that the concept of red is not red). In other words, the initial supposition is that this is simply  the fact  about the concept of the "impredicable" (that is, according to the first alternative it is assumed that the concept of the "impredicable"  has  this property (namely that it is "impredicable"), i.e., it happens to have this property, if we like it or not.
In what way, however, are we going to  express  (in the sense of intend )  or signify  this fact  about the concept of the "impredicable"?
Presumably, the only way is to say that it is "impredicable". Yet  this way of expressing  the fact about the concept, namely the fact :  the concept of the "impredicable" is "impredicable"  has the effect of making that concept appear to meet the one and only criterion of being a "predicable" concept.
But can we say, then, that the concept is  in fact  a "predicable" concept? Propbably not. On the contrary, the original supposition still stands, namely that the concept is in fact "impredicable". Accordingly, it would seem to be  only  in  our mode of expressing or signifying  this fact that the concept is given the appearance of being "predicable", whereas  in fact  it is of course "impredicable" (according to the first alternative). And this does not amount to a contradiction :  The concept of the "impredicable"  is  really and in fact  "impredicable" (according to the first alternative) and (is)  not-"impredicable"  (that is, "predicable")  only in virtue of our mode of expressing or signifying  what is so really and in fact ( NOTE 36 ).
Indeed, this conclusion would seem to be confirmed if, as a result of our mode of expressing the fact about the concept of "impredicability", we were simply to enunciate the proposition :

This concept is now seen to be "predicable"

Such a proposition would, of course, be true, since the requirements for "predicability" have certainly been met in this case. Yet what would we mean by this statement just given? We could only mean that the concept of "impredicability" was really and in fact "impredicable". Why? Because if the concept were not really "impredicable", we could not possibly say that is was "predicable".
In other words, its  seeming  "predicability" necessarily presupposes its  real  "impredicability". Accordingly, the supposed "predicability" of the concept can only be interpreted as meaning that while the concept is  really  "impredicable", nevertheless  in  stating or intending  the fact we necessarily give it the  appearance  of being "predicable". The negation of "predicability", as it is expressed in "impredicability", causes the impossibility of adequate expression (in the sense of intention).

How can it be, that, apparently having only two alternatives, viz., "impredicable" and "predicable", as a property of the concept of the "impredicable",  "predicable" and "impredicable" taken together do not constitute a contradiction?
Well, a good example indicating that this can be so concerns  non-being :  If we speak about non-being, then our way of expressing it gives the appearance of the  being  of non-being, although we know that non-being does not exist.
Similarly, in the case of concept of the "impredicable", in treating of it and intending it, we inevitably give it the appearance of being a "predicable" concept. Yet this does not mean that it  really  is a "predicable" concept, any more than, mutatis mutandis, our treating of and talking about, non-beings means that non-being really is a being.

Up to now, in our discussion of the solution of the paradox, we have considered only the first alternative of answering the question :

Is the concept of the "impredicable" itself "impredicable" or "predicable" ?,

namely the supposition that it was "impredicable". Here we did, following the expositions of VEATCH, not encounter a contradiction (which already means that there cannot be a paradox).
So what if our initial supposition were that the concept of the "impredicable" was "predicable" rather than "impredicable" ?
Investigating this, at the same time decides the question whether the concept of the "impredicable" is "impredicable" or "predicable" (See where we had mentioned this further investigation as to deciding this question, namely HERE ).
Consider what must be meant by the assertion that the concept of the "impredicable" is itself a "predicable" concept. Presumably, according to the present supposition, one would mean by this that the concept was itself  really and in fact  "predicable". Yet is this a possible meaning after all? To say that the concept of the "impredicable" is itself "predicable" means that this concept applies not only to its objects in first intention, but also to these objects taken in second intention.
To be sure, the concept of the "impredicable" is the concept we have of "impredicable" concepts.
So our second alternative states in fact that the concept of "impredicable" (concepts) is itself an " impredicable" concept. But we said that our second alternative stated that the concept of "impredicable" (concepts) is a "predicable" concept. So this second alternative is a downright contradiction (and thus the first alternative -- which did not entail a contradiction -- is affirmed thereby).
All this means that the only way in which the concept of the "impredicable" could be  said  to be "predicable" would be for it  really  to be "impredicable". Vice versa, were it not "impredicable"  really,  there would be no possible sense in which it could be  said  to be "predicable".
Apparently, then, supposing the concept to be "predicable" leads us right back to the same situation which we found to prevail when we supposed the concept to be "impredicable". That is to say, the concept of the "impredicable" must be considered to be "impredicable"  really.  And only secondarily and derivatively, and in virtue merely of our mode of signifying or expressing this fact of its "impredicability", can it be  said  to be "predicable". Hence the initial supposition (that is, the second alternative) that the concept is "predicable" must be interpreted to mean that it is "predicable" not really, but only in virtue of the necessary and inescapable means that we must employ to express what it really is  ( VEATCH, p.148 ).
Indeed, should we try to interpret our initial supposition (the second alternative) as to the "predicability" of this concept as meaning that it  really  is a "predicable" concept in itself and in fact, then we should be led into a contradiction, as we have shown above. Moreover, such a contradiction does not effect a paradox, since it is quite possible to avoid it, namely by accepting the first alternative.

This, then, is VEATCH's proposal for a solution of the conceptual paradoxes. He himself adds (p.149) :

That it may not bear scrutinity I am well aware. Yet whatever may be the shortcomings of this particular solution, I believe that this general approach to the problem of the paradoxes is likely to prove much more fruitful than the sort of approach that has generally been followed by the mathematical logicians. Merely because the so-called "predicability" of concepts would appear to give rise to paradox in one single instance would scarcely seem sufficient warrant for ruling it out altogether.

We have seen that "predicability" in the case of the concept of  (a) being  does not lead to any problem whatsoever. It is only the "predicability" of the concept of the  "impredicable"  that gives rise to problems when we ask for whether it is "predicable" or "impredicable" (a problem, that is to say, if we would not accept the solution given above).
VEATCH, p.149, therefore, continues :

Indeed, even if one were ultimately forced to admit that the paradoxes cannot be solved in the strict sense, but can only be evaded by positing a sort of  ad hoc  rule, then why should such a rule be so phrased as to exclude the possibility of "predicability"  [  ( NOTE 37 ) my note]  just as such? why not simply exclude "predicability" or self-memberedness in the one instance where they prove to be embarrassing -- viz., in the instance of "impredicable" concepts or of nonself-membered classes? After all, if problems must be dealt with by what is no better than arbitrary fiat, then it would be well, it would seem, for such a fiat to be of as limited a scope as possible.

the concept of "impredicable" is "impredicable" (or "predicable") ( NOTE 38 ).

Let us investigate whether this proposition is completely self-referential or not.
In order to determine this we look first to the proposition :

the concept of red is an "impredicable" concept.

This proposition can be the conclusion of the following argument ((A)(B)(C)) :

(A)  If the concept of X is not itself (an) X, then the concept of X is an "impredicable" concept (or, equivalently, the concept of X is "impredicable").

(B)  The concept of red is not itself red.

(C)  (Conclusion) The concept of red is an "impredicable" concept.

the concept of red is an "impredicable" concept,

which is an intending subject-predicate proposition, refers to something else, namely its meaning or ground which is expressed by the proposition (B) :

the concept of red is not itself red.

So our proposition ((C)) does not refer to itself. It intends (B). It refers non-contradictionally to its meaning.

the concept of a being is a "predicable" concept.

This also can be the conclusion of an argument ((D)(E)(F)) :

(D)  If the concept of X is itself (an) X, then the concept of X is a "predicable" concept.

(E)  The concept of a being is itself a being.

(F)  (Conclusion)  The concept of a being is a "predicable" concept.

the concept of "impredicable" is itself "impredicable".

Nevertheless, also this proposition can be the conclusion of an argument ((G)(H)( I )) :

(G)  If the concept of X is not itself (an) X, then the concept of X is an "impredicable" concept.

(H)  The concept of "impredicable" is not itself "impredicable".

( I )  (Conclusion)  The concept of "impredicable" is an "impredicable" concept.

The concept of "impredicable" is itself "impredicable".

And the truth of this proposition should (like in te previous examples) be based on the second proposition ((H)) of the argument, namely the proposition :

The concept of "impredicable" is not itself "impredicable".

So the ground of our proposition is its opposite! This means that it cannot be its ground. And thus the ground of our proposition

the concept of "impredicable" is itself "impredicable"

can only be itself.  That is, its meaning is itself, or, said differently, it intends itself, it refers to itself, and it refers to itself totally and exclusively. So this proposition embodies total self-reference.

the concept of "impredicable" is itself "predicable".

This can again be the conclusion of an argument ((J)(K)(L)) :

(J)  If the concept X is itself (an) X, then the concept X is "predicable".

(K)  The concept of "impredicable" is "impredicable".

(L)  (Conclusion)  The concept of "impredicable" is itself "predicable".

So in both cases (viz., the concept of "impredicable" being either "impredicable" or "predicable") we end up with total self-reference.

If something has total self-reference (that is, is totally self-referential, and thus not also referring to some other things), then it, with all its (atomic) notions, refers to all its notions, and, moreover, every such notion (referring) to its proper corresponding notion, that is, to itself.
Now we can reasonably assert that an entity, if it wants to be a genuine entity (of whatever sort), cannot be totally self-referential, because it cannot  refer  to something and at the same time  be  that same something. The reference here does not go, as it should, from, say, A to B, but from A to A, which means that there is no reference at all, which in turn is equivalent to the fact that there is no meaning :  An entity embodying total self-reference has no meaning, it is meaningless.
The S-P predications

the concept of the "impredicable" is "impredicable"

and

the concept of the "impredicable" is "predicable"

have no meaning, no significatum. Therefore they are not S-P predications at all. So the question whether the concept of "impredicable" is "impredicable" or "predicable" is meaningless. Therefore this question should be ruled out from Logic, without, however, ruling out with it all other "predicable" concepts  ( The concept of a being, for example, is a "predicable" concept. It does not generate a paradox, so it must be retained in Logic).

Let this be sufficient for understanding the "impredicable" paradox, and its status in an intentional Logic.

This paradox, because it is a propositional (in contrast to a conceptual) paradox, should be treated of in the (main) Section on the Proposition. However, it is a paradox, and the economy of exposition (we here following VEATCH) seems more or less to demand to treat it here.
The solution of it, here presented, is not discovered by me, neither by VEATCH, but is a common one  ( VEATCH, p.149 ).

There are two formulations of this paradox, of which only the second one is a geuine paradox.
The first formulation runs as follows :
( Epimenides the Cretean, makes the statement :)

Every statement made by a Cretean is a lie.

If this is to be a paradox, then both alternative answers as to the truth or falsity of this proposition, must be a contradiction.
Well, let us first try the answer saying that it is true.
If it is true, then it must be false, because it is a statement made by a Cretean. So here we have a contradiction.
What is involved is simply a generalization which includes itself within its own scope. However, what is asserted in the generalization is in effect a denial of that generalization itself (that is, that it is not an all out generalization, because some things which should be subsumed under it are excluded), because we have assumed that the assertion is true.
If, on the other hand, we take the second alternative, namely that the statement is false, then there must be at least one statement, made by a Cretean, that is true. And this (true statement) must not necessarily be the particular statement made by Epimenides. So his statement could indeed be false, as was indeed assumed in the second alternative. So here no contradiction is involved, which means that this formulation of the paradox does not embody a paradox.

Of course, if one follows Russell in prescribing a hierarchy of types and hence in proscribing any self-membered classes or any "predicable" concepts, then one could not permit in any system of Logic a generalization which included itself in its own scope. However, as we have found from earlier discussions (based on VEATCH), such prescriptions and proscriptions are alike unnecessary and embarrassing. In fact, on the basis of VEATCH's classification of such "predicable" concepts and self-membered classes, a statement about all statements would fall in the second group, i.e., in the group not of the analogous or of the negative concepts but of the second-intentional or logical entities (and they are perfectly legitimate). For in the case of these latter, it is quite possible for an intention to intend its object taken both in first and in second intention :  A concept of a concept is itself a concept (a concept X intends an object Y in first intention, while the concept of this concept intends Y in second intention). A proposition about a proposition is itself a proposition, etc. Accordingly, if such "predicable" concepts and self-menbered classes are permissible and possible, then the generalization made by Epimenides will be formally and structurally quite legitimate.
To be sure, when the generalization is made, it turns out in the  particular  case to be self-contradictory, namely in the case where we assume his statement to be true. Yet for this reason it is not meaningless  ( VEATCH, p.150), and is thus not a paradox.

On the other hand, the second formulation of the liar constitutes a complete self-reference. It reads :

the proposition which I am now enunciating is false.

Obviously, if this proposition is true, it is false. And if it is false, it is true. So both alternatives involve a contradiction, hence the statement is a paradox.
Because this proposition contains two assertions, namely the assertion that I now assert something, and the assertion that it is false, a better formulation of the liar paradox is the following :

this proposition is false.

Again, if it is true, it is false. And if it is false, it is true. So we also here have to do with a paradox.

Nevertheless, the paradox may here be avoided simply by recognizing that the proposition in question is not really a proposition (and only with a proposition truth or falsity are relevant). The reason why it is not a proposition is because the subject term  ' this proposition '  does not in fact refer to the proper subject of  ' (is) false ',  because this proper subject is not here identical to  ' this proposition '  (which is the grammatical subject), but to :  ' this proposition is false ',  that is, to the whole proposition. But, conceding this, we still cannot say :

this proposition is false  is  false,

because this doesn't mean anything (and, again, the proper subject is the whole proposition). So the predicate  ' (is) false '  has no subject, and therefore the alleged proposition is not a proposition at all, and thus there is no paradox :  We are fully entitled to eliminate it from Logic. Indeed, the predicate in :  ' this proposition is false ',  namely  ' (is) false ',  is totally included in its proper subject, which is :  ' this proposition is false '.  So there is no conceptual separation (and subsequent re-uniting) of subject and predicate. Here the whole proposition is its subject, which means that the proposition is entirely about itself and about nothing else. It is, as every proposition, about its subject. But here this subject is the whole proposition. So we here have a clear case of complete or total self-reference, and therefore  ' this proposition is false '  cannot be a genuine logical intention such as a genuine subject-predicate proposition, and should be ruled out of intentional Logic.

So the first formulation of the liar turned out not to be a paradox because it involves just a contradiction (which can be avoided by taking the other alternative), and thus not meaningless, and the second formulation of the liar is not a paradox because it is meaningless :  The alleged proposition is not a proposition at all, so truth or falsity cannot be a feature of such a 'proposition'.

The first formulation of the liar (viz., every statement made by a Cretean is a lie )  could be rephrased as follows :

Every generalization I make is false   (calling this statement LIAR)

Here -- in the case where we are considering this very proposition itself as one of the many possible instantiations -- also we have a predicate  ( ' (is) false ' )  without a proper subject, because also here the (logical) subject is the whole proposition. Earlier we asserted that this, and indeed all the formulations equivalent to the first, do have meaning. Now, however, it seems not to be so, because of the absence of a proper (i.e., logical) subject. But this is only apparently so. The predicate  ' (is) false '  does in the case of LIAR (that is, the above proposition) not have a proper subject, but this predicate is not only said about

Every generalization I make is false

(which is indeed a generalization because of "every"), but (according to this very statement) also about any other generalization I make. One such a generalization could be for example :

Every sponge is an aquatic organism

(that is, not only this particular sponge is an aquatic organism, but all sponges are). This generalization is logically permitted :
' Every sponge '  is the subject, and about this subject it is asserted that it is an aquatic organism. So the predicate  ' (is) an aquatic organism '  has a genuine subject, that is, a logically proper subject ( NOTE 39 ).
And even when we must exclude the particular generalization  ' every generalization I make is false ',  by reason of the fact that it is not a genuine proposition, that is, even when we must exclude one particular case from all the cases intended by the statement  ' every generalization I make is false ',  the statement itself still has meaning. If we exclude from the extension of LIAR -- whose extension is constituted by the set of all generalizations I make -- precisely the one generalization  ' every generalization I make is false ',  then LIAR is a genuine subject-predicate proposition that intends all generalizations I make, except the generalization  ' every generalization I make is false '.  What is excluded is one item in the extension of LIAR.  LIAR itself is retained, retained as the intending proposition. Indeed, when we have excuded LIAR from its extension, the intending proposition  ' every generalization I make is false '  has become a genuine logical S-P proposition, because now the predicate  ' (is) false '  has a proper subject. And indeed, the proposition  ' every generalization I make is false '  means that all generalizations I make are false, except the generalization  ' every generalization I make is false '  (which I have made), where "except" here means that this latter statement will not be allowed to be a member of the extension of it. It is, however, retained as the intending proposition.

This concludes our exposition about the logical paradoxes.
It also concludes our discussion of the concept.

e-mail : 
( Please write in  ' Subject '  entry :  ' METAPHYSICS ',  in order for me to be able to distinguish your mail from spam )

Back to Homepage

Back to Contents

Back to Aristotelian metaphysics Part I

Back to Aristotelian metaphysics Part II

Back to Aristotelian metaphysics Part III

Back to Aristotelian metaphysics Part IIIa

Back to Aristotelian metaphysics Part IV

Back to Aristotelian metaphysics Part V

Back to Logic Part I

Back to Logic Part II