

e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam ) The basic theory of proof in mathematical Logic.
Until now in our discussion of the theory of argument or inference we have occupied ourselves more with the question of what mathematical logicians have considered to be examples of argument than with any actual theory of argument as such.
So, what is it in the various types of relations that guarantees, according to the mathematical logicians, the validity of the conclusion and entitles the relation to be reckoned an actual pattern of inference? It is, so they say, that the argument or proof is necessarily something purely formal. In other words, the key to an understanding of the mathematical logician's theory of argument would seem to be the notion of a purely formal argument. What, then, is an argument that is purely formal, or that holds simply in virtue of its form?
Let us direct our attention to the mathematical logician TARSKI where he sets forth some axioms and theorems for a system having to do with the congruence -- symbolized by 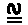 -- of line segments.
-- of line segments.
Suppose we are interested in general facts about the congruence of line segments, and we intend to built up this fragment of geometry as a special deductive theory. We accordingly stipulate that the variables "x", "y", "z", ... denote segments. As primitive terms we choose the symbols "S" andAs for the proof of the theorems, see our derivation of them above with respect to a more general case (the relation R which is reflexive and having property P ).. The former is an abbreviation of the term "the set of all segments", the latter designates the relation of congruence, so that the formula :
x y
is to be read as follows :
the segments x and y are congruent. Further we adopt only two axioms :
Axiom I. For any element x of the set S, xx (in other words : every segment is congruent to itself).
Axiom II. For any elements x, y, and z of the set S, if xz and y
z, then x
y (in other words : two segments congruent to the same segment are congruent to each other).
Various theorems on the congruence of segments may be derived from these axioms, for instance :
Theorem I. For any elements y and z of the set S, if yz, then z
y.
Theorem II. For any elements x, y, and z of the set S, if xy and y
z, then x
z.
(quoted in VEATCH, p.223/4 )
Our knowledge of the things denoted by the primitive terms, that is, of the segments and their congruence, is very comprehensive and is by no means exhausted by the adopted axioms. But this knowledge is, so to speak, our private concern which does not exert the least influence on the construction of our theory. In particular, in deriving theorems from the axioms, we make no use whatsoever of the knowledge, and behave as though we did not understand the content of the concepts involved in our considerations, and as we knew nothing about them that had not been expressly asserted in the axioms. We disregard, as it is commonly put, the meaning of the primitive terms adopted by us, and direct our attention exclusively to the form of the axioms in which these terms occur.Here we have -- as VEATCH responds to this consideration of TARSKI's -- a concrete example of how a proof may be formalized, and once it is so formalized, one can presumably see how the actual argument itself is simply a matter of form ( NOTE 48 ). That is to say, its validity has nothing to do with its content or with what it is about. In the example from TARSKI the argument or proof does not have to be about line segments and their congruence.
This implies a very significant and interesting consequence. Let us replace the primitive terms in all axioms and theorems of our theory by suitable variables, for instance, the symbol "S" by the variable "K" denoting classes, and the symbolby the variable "R" denoting relations (in order to simplify the considerations, we disregard here any theorems which contain defined terms). The statements of our theory will then be no longer sentences, but will become sentential functions which contain two free variables, "K" and "R", and which express, in general, the fact that the relation R has this or that property in the class K (or, more precisely, that this or that relation holds between K and R, cf. Section 27). For instance, as it is easily seen, Axiom I and Theorems I and II will now say that the relation R is reflexive, symmetrical and transitive respectively, in the class K. Axiom II will express a property for which we do not have any special name and to which we shall refer as property P. This is the following property :
for any elements x, y, and z of the class K, if xRz and yRz, then xRy.
Since, in the proofs of our theory, we make use of no properties of the class of segments and of the relation of congruence but those which were explicitly stated in the axioms, every proof can be considerably generalized, for it can be applied to any class K and any relation R having those properties. As a result of such a generalization of the proofs, we can correlate with any theorem of our theory a general law belonging to the domain of logic, namely to the theory of relations, and stating that every relation R which is reflexive and has the property P in the class K also has the property expressed in the theorem considered. So, for instance, the following two laws of the theory of relations correspond to Theorems I and II :
I '. Every relation R which is reflexive in the class K and has the property P in that class is also symmetrical in K.
II '. Every relation R which is reflexive in the class K and has the property P in that class is also transitive in K.
Insisting on the intentionality of logical entities and thus on the duality of intending and intended, entails that we must hold that the generalization of the object of a proof does not, as an effect, entail the formalization of the proof itself : Whether the object of proof is generalized or not, the form of the proof remains (ultimately) a syllogism. And the form in turn of the syllogism is the relation of (triple) identity.
The mathematical logicians hold that when the object of a proof is maximally generalized all meaning is removed except what is laid down explicitly in the axioms and theorems of the system, for instance that, say, the relation R, characterizing the object of proof, that is, the particular unity of order about which the argument handles, is supposed to have certain properties such as, for instance, reflexivity, as laid down in one of system's axioms, or that the system is such that (or is such that it is at least relevant to hold that) xRy and yRz, where x, y, and z are elements of the system, or is such that 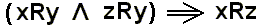 , etc.
, etc.
And when so stripped of meaning, the bare form of the argument is revealed. The argument is then nothing more than a syntactical entity.
But, when we insist on intentionality, we see that it is the object of proof that is being formalized (in the sense of having a minimum of meaning, or no meaning at all), not the proof itself.
The rules of inference are the rules of syllogistic arguments, where these rules are expressed as the many existing types of syllogistic arguments, for instance the simple (that is non-compound) syllogisms, i.e., syllogisms where the premises and conclusion are single (that is, non-compound) subject-predicate propositions, or compound syllogisms such as the modus ponens syllogisms (where the major premise consists of a compound (conditional) proposition (such as ' if x is a man, then it is mortal ' ), etc. In all syllogisms, I venture to say, the ultimate rule is that of (triple) identity.
In simple syllogisms this (triple) identity is directly visible :
S is M, M is P, therefore S is P.
Here, S, M, and P are terms (that is, not propositions).
In compound syllogisms the (triple) identity is not directly visible, but can be revealed. So in the compound syllogism that is called the modus ponens. Here the elements are not terms but (subject-predicate) propositions :
p ==> q
p
---------
q
and, when analyzed :
(A is B) ==> (A is D)
(A is B)
------------------------
(A is D)
For example :
If virtue is knowledge, virtue can be taught ( = virtue is teachable).
Virtue is knowledge.
--------------------------------------
Virtue can be taught.
To reveal the relation of triple identity we consider the unity of order R.
When we say ' R is p ', we mean : The unity of order R is such that the proposition p holds. Here " The unity of order R " is the subject term, "is" the copula, and "such that the proposition p holds" the predicate.
And when we say ' R is p ==> q ', we mean : The unity of order R is such that the proposition p ==> q holds, that is, this unity of order is such that if the propsition p holds, then also the proposition q.
Now we reveal the relation of triple identity in
p ==> q
p
---------
q
:
R is p ==> q
R is p
---------------------
R is q
In words :
R is such that if p holds, then also q.
Well, R is such that p holds.
Therefore, R is such that q holds.
We can state this in an equivalent way as follows, where B is a type of thing (s.l.), D is a property, and A is an individual thing (s.l.) :
B is D for all B
A is B
-----------
A is D
That is : All B's are D, A is such a B, therefore A is D.
For example :
Whatever is knowledge IS such that it can be taught.
Virtue IS knowledge.
----------------------------
Virtue IS such that it can be taught.
Whether such conversions are really possible for all types of compound syllogisms, we do not know, but assume it to be so. And thus on the basis of this assumption we state that the fundamental form of all syllogisms is the relation of (triple) identity. And, as has been said, this form, will not change when we 'formalize' the object of the proof.
and finally to
So, while the proof or argument itself is not formalized as a result of not considering the meaning of the symbols, its formal structure is made visible by such non-consideration of meanings.
The class and propositional calculi ( = predicate Logic, respectively propositional Logic).
About classes we have spoken already earlier, so a few words will suffice here.
The relation of class inclusion is a transitive relation. Yet, as we saw earlier, this by no means implies that it is an intentional relation, any more than, say, the relation ' greater than ' is an intentional relation merely because it is transitive.
Of course, as an instrument for determining the inclusive designation of concepts in propositions, the class calculus can be of real service so far as intentional Logic is concerned. But beyond this, its pertinence should not be overestimated.
The propositional calculus.
For the propositional calculus the ultimate elements (which it manipulates) are single propositions (and thus not things like subject terms, copulas, or predicate terms) and it investigates the connections of propositions, this connection resulting in compound propositions. One special sort of 'compounding' is adding to a given proposition its negation. So the propositional calculus investigates the logical connectives "and", "or", "not", "if-then", and "is equivalent to". Some combinations of propositions, regardless their meaning, imply other combinations of (those same) propositions, or are equivalent to other such combinations. Such assertions of implication or equivalence can be proved to be always true, regardless the meaning of the constituent propositions. They are thus tautologies and are as such the theorems of the propositional calculus.
These theorems are of much greater interest and relavance for intentional Logic than are the tenets of the class calculus. To be sure, we think that in the propositional calculus as elsewhere, the mathematical logician has dealt with propositional relations in such a way as in effect to transform them into nonintentional relations. Further, he has also failed to recognize the peculiar character and import of most of the theorems presented in the calculus, by not regarding intentionality, that is, by not regarding what precisely is intended by these theorems. Yet for all that, the propositional calculus, when properly interpreted, should prove to be a much needed adjunct to an intentional Logic.
Truth-functional interpretation and intentional interpretation of the propositional calculus.
In mathematical Logic the truth of compound propositions is universally made dependent on the truth of the component propositions.
When we first consider conjunctions and negations this truth-functionality looks natural.
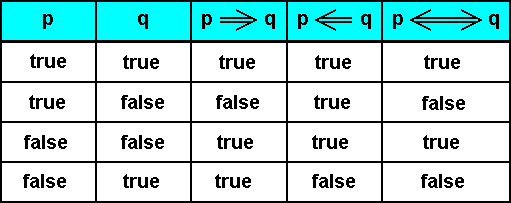
The truth table for the conjunction 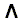 (which means "and") of the propositions p and q is (defined as) :
(which means "and") of the propositions p and q is (defined as) :
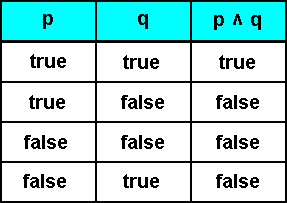
Indeed, 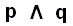 can only be true if both p and q are true.
can only be true if both p and q are true.
And for negation the truth table for not-p, symbolized by 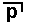 , is (defined as) :
, is (defined as) :
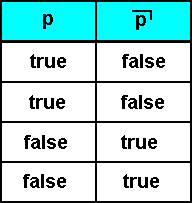
Where p is a proposiition.
Also this looks fair enough.
But with disjunction things are already different. Indeed, as we saw earlier, for the disjunction 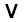 , meaning "or", as in
, meaning "or", as in 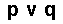 , there can be given two truth tables which both seem natural :
, there can be given two truth tables which both seem natural :
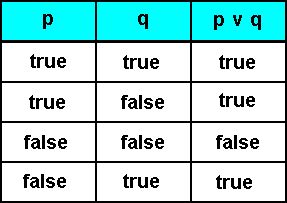
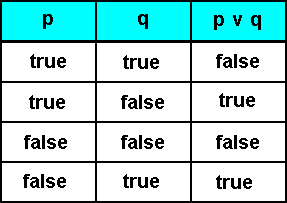
This renders the truth-functionality of disjunctions to be a matter of mere arbitrary agreement.
But when we come to implication, symbolized by  , things go awry indeed.
, things go awry indeed.
The truth table for  , where p are q are propositions, is defined by the mathematical logicians as :
, where p are q are propositions, is defined by the mathematical logicians as :

This truth table says that p ==> q is always true, except when the condition is true and at the same time the conditional false.
On the other hand, according to intentional Logic an implication should intend a possible state of affairs, expressed by the proposition q, that will necessarily follow from another state of affairs, expressed by the proposition p, were such a state (p) existing. So the truth of p ==> q depends, not on the truth of p and q, but on their meaning. For instance, let p mean : x is a man, and q mean : x is mortal. p ==> q then means : if x is a man, then x is mortal.
And we know, for this implication to be true, that the following must be presupposed : All men are mortal. Now indeed, when ' x is man ' is true, that is, when x belongs to the class signified by the subject of the presupposition, then surely it follows that x is mortal, that is, when p is true, it follows that q is true, and this means that then p ==> q is true, i.e., it is true that q is implied by p. So the truth of p ==> q depends, to be sure, on the truth of p and q, but it, taken as just ' if x is a man, then it is mortal ' (p ==> q), does not depend on these truths alone, for even if it is true that x is a man, and that x is mortal, the fact that x is a man does not necessarily entail that x is mortal.
This being mortal (as asserted in the considered-to-be-true proposition ' x is mortal ' ) could be a fact accidentally coexisting with the fact that x is a man. So while the truth of the propositions ' x is a man ' (p) and ' x is mortal ' (q) is sufficient for the conjunction 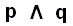 to be true, it is not sufficient for the implication
to be true, it is not sufficient for the implication  to be true, while according to the truth-functional interpretation it is sufficient (see the first entry of the truth table for implication given above). This latter truth, that is the truth of p ==> q, also depends on what ' x is a man ' means, that is, what ' man ' means. And only when we learn to know the nature of man insofar relevant for our case, that is, such that this nature necessarily brings with it that it is a bearer of the property 'being mortal' -- and this knowledge is expressed in the presupposed and, consequently, to be added, proposition ' all men are mortal ' -- we will acknowledge the proposition ' if x is a man, then x is mortal ', that is, p ==> q, to be true. We will acknowledge it because we now know that being mortal necessarily flows from being a man (we know it as long as we assume the truth of ' all men are mortal ' ).
to be true, while according to the truth-functional interpretation it is sufficient (see the first entry of the truth table for implication given above). This latter truth, that is the truth of p ==> q, also depends on what ' x is a man ' means, that is, what ' man ' means. And only when we learn to know the nature of man insofar relevant for our case, that is, such that this nature necessarily brings with it that it is a bearer of the property 'being mortal' -- and this knowledge is expressed in the presupposed and, consequently, to be added, proposition ' all men are mortal ' -- we will acknowledge the proposition ' if x is a man, then x is mortal ', that is, p ==> q, to be true. We will acknowledge it because we now know that being mortal necessarily flows from being a man (we know it as long as we assume the truth of ' all men are mortal ' ).
So it is clear that (at least) implication cannot be defined truth-functionally, which in turn means that we cannot ignore the semantic aspect or part : The truth of p ==> q depends first of all on the meaning of p and of q.
If we do not consider implication according to the lines just given, but simply follow its truth table , we see that also in it we have the implication p ==> q true when both p and q are true.
But what, then, when p meant ' two plus two is four ', and q meant ' New York is a large city ' ? Here also both propositions are true. But then, according to mathematical Logic (as long as implication is still defined in it according to the truth table given above) the proposition ' if two plus two is four, then New York is a large city ' is also true. And this is, of course, nonsense.
But not only this proposition, but also the proposition ' if two plus two is five, then New York is a large city ' is, according to the truth table for implication , true, because here p ( ' two plus two is five ' ) is false, and q ( ' New York is a large city ' ) is true.
And also the proposition ' if two plus two is five, then New York is a small city ' would be true according to the truth table, because both p and q are false.
Here we clearly see that the truth of p ==> q depends on the meanings of p and q, and not solely on their truth or falsity. The proposition ' if two plus two is five, then New York is a large city ' should be false (instead of true). It should be false because of what p and q mean : New York being a large city cannot in any way be dependent on, or follow from, the absence of something corresponding to two plus two is five ( = ' two plus two is five ' being false). And also it cannot be dependent on, or follow from, the presence of something corresponding to two plus two is four ( = ' two plus two is four ' being true).
It is by its very nature that, if it is to perform its proper intentional function, an implicative compound proposition involves a connection in meaning between its component propositions. Indeed, to assert an implicative compound proposition is not to assert the truth of the component propositions in the case of a hypothetical implicative compound (if p, then q ), and not merely to assert the truth of the component propositions in the case of a categorical implicative compound (because p, q ). Rather it is to assert precisely this sequence of the one proposition upon the other, or the connection in meaning between the two. Accordingly, by his insistence on the truth-functional interpretation of such implicative compounds the mathematical logician in effect suppresses their peculiar intentional function altogether.
And also attempts to remedy absurdities like the ones given above by altering the truth table for implication, will not tough the real issue at stake here.
And because there are now, as we have just seen, at least two connectives (disjunction and implication) to which truth-functionality does not properly apply, we should realize that truth tables have nothing intrinsically to do with compound propositions (they only happen to be in accord with conjunctions and negations). For every compound proposition we must ask what precisely it is supposed to intend, that is, what the component propositions mean, and only then we can determine whether that compound proposition is true or false. It is in this way that the propositional calculus must be revised in order for it to become compatible with intentional Logic.
This, however, must be qualified further.
Let us concentrate on implication, and consider some examples.
When defining implication we must, as we already found out, take into account intentionality, that is we must take into account meaning. So the definition of implication cannot rely solely on some truth table.
Indeed, we must stipulate that the implication p ==> q means that there must be a term in the proposition q, of which the significatum ( = that what the term signifies) necessarily flows from the significatum of a term in the proposition p.
Let's consider the following instance of p ==> q :
If x is a man (that is, a human being), then x is capable of laughing.
Here ' x is a man ' stands for p, while ' x is capable of laughing ' stands for q.
Let us further reproduce here the truth table for implication :

In the consequent (proposition) of our (compound) hypothetical proposition ' If x is a man, then x is capable of laughing ' we find the predicate term ' capable of laughing '. And it is evident that what our hypothetical proposition asserts is that the significatum of this predicate term necessarily flows from the significatum of the term ' man ', which is the predicate term of the antecedent proposition of our compound proposition. Because capability of laughing necessarily flows from being a man (and perhaps could flow from other essences as well), we can confidently say ' If x is a man, then x is capable of laughing '. So by finding out what is presupposed by the hypothetical proposition, namely the truth of the proposition ' All men are capable of laughing ', we are able to d e f i n e (not arbitrarily) implication.
That what is signified by the component proposition ' x is a man ' is a (sufficient) condition (perhaps one of the many sufficient conditions) for the truth of the other component proposition ' x is capable of laughing '.
While the truth of the consequent proposition ' x is capable of laughing ' depends on the truth of the antecedent proposition as signifying one of the sufficient conditions, it is clear that the implication (that is, the whole compound proposition) is still true when the proposition ' x is a man ' is false, for example when x is not a man but an insect. This is so because our implication only says that if x is a man, then x is capable of laughing. This still being true of the implication, despite the falsity of its antecedent, is expressed in the last two entries of the truth table of implication. Indeed, when the proposition ' x is capable of laughing ' is true, while the proposition ' x is a man ' is not, this still does not affect the truth that if x is a man, then x is capable of laughing : x is an insect, and, as it has turned out, it is capable of laughing, but whether this capability is rightly (fourth entry of truth table) or wrongly (third entry) assessed in the case of the insect, the fact remains that if it were a man, it would surely be capable of laughing. This is expressed in the third and fourth entries of the truth table.
And of course when the proposition ' x is a man ' is true and also the proposition ' x is capable of laughing ' is true, then the implication is true. It is then true by definition. This is expressed in the first entry of the truth table.
On the other hand, when the proposition ' x is a man ' is true, but the proposition ' x is capable of laughing ' false, then the implication is false, because now the definition of ' implication ' is violated.
Another instance of p ==> q is :
If the electromagnet is switched on, then iron will be attracted toward it.
Here also we have a real dependence of being attracted on the electromagnet being switched on.
And indeed, whether the electromagnet is actually being swiched on or not (that is, whether the proposition ' the electromagnet is switched on ' is true or not, the implication is true, except when, while it is true ( = the electromagnet being switched on), the proposition ' iron will be attracted toward it ' is false ( = iron will not be attracted toward it), because then the definition of the implication is violated.
From all this it should be clear that from the viewpoint of intentional Logic a truth table cannot constitute the (non-arbitrary) definition of implication (or of any other connective for that matter). Things are such that the truth table (as given above) holds as a result of the definition of implication. And the definition of implication as (implication figures) in the compound proposition p ==> q (where p and q are single propositions, each intending some state of affairs) is :
There is a term in the consequent proposition q, of which the significatum necessarily flows from the significatum of a term in the antecedent proposition p.
And from this non-arbitrary definition (which takes meaning into account) of implication, the validity of the truth table for implication follows.
Having found how things are in the case of implication, they should mutatis mutandis be the same for the other logical connectives :
The definition of conjunction (that is, of the connective "and") as (conjunction figures) in the compound proposition 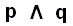 (where p and q are single propositions, each intending some state of affairs) is :
(where p and q are single propositions, each intending some state of affairs) is :
The significatum of the component proposition q accidentally coexists with the significatum of the component proposition p.
And from this non-arbitrary definition (which takes meaning into account) of conjunction, the validity of the truth table for conjunction (as given in mathematical Logic) follows :

The first entry of this table expresses the definition of ' conjunction '.
The other entries express the non-coexistence of the states of affairs signified by the component propositions p and q.
Coexistence, here, is only an accidental coexistence, otherwise, i.e., when the coexistence is a necessary coexistence, the connective would not be "and" but rather "is equivalent to" (double implication). We see that such a thing like accidental coexistence (and also of course, necessary coexistence) cannot be expressed by whatever truth table all by itself. We must take into account what (in extramental reality, or in a 'reality' considered as if it were extramental, because objective) is intended by the compound proposition, implying that the propositional calculus (and with it the whole of Logic) cannot be a self-contained system. Well, it can be (transformed into) a self-contained system, but then it is not part of genuine Logic anymore, as long as Logic is supposed to be the science about the formal instruments of knowledge (of knowable things).
The definition of (exclusive) disjunction (that is, of the connective "or") as (disjunction figures) in the compound proposition 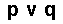 (where p and q are single propositions, each intending some state of affairs) is :
(where p and q are single propositions, each intending some state of affairs) is :
Either the significatum of the component proposition q exists, or the significatum of the component proposition p exists, but not both at the same time.
or, (defining) equivalently :
If and only if the significatum of the component proposition p does not exist, the significatum of the component proposition q does exist. And if and only if the significatum of the component proposition q does not exist, the significatum of the component proposition p does exist.
And from this non-arbitrary definition (which takes meaning into account) of (exclusive) disjunction, the validity of the truth table for disjunction follows :

In the light of the definition of (exclusive) ' disjunction ' this truth table (as given in mathematical Logic) speaks for itself.
And if want to do so, we can, in addition to this exclusive "or" define inclusive "or", the truth table of which was given above, and is here reproduced :

The connective "equivalence" is a double implication, that is, an implication that goes both ways. So
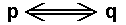 means :
means :The significatum of a term in the component proposition q necessarily follows from the significatum of a term in the component proposition p, and vice versa with respect to these same significata.
Because the definition of equivalence is totally based on that of implication, we can derive the truth table of equivalence from that of implication, by combining the implication which goes to the right with that which goes to the left :
resulting in the truth table of equivalence (as given in mathematical Logic) :
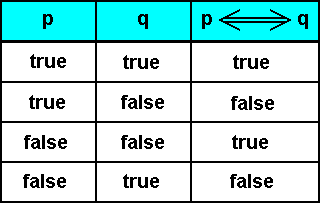
The table here expresses the definition (of equivalence) by assigning truth to a compound proposition with its component propositions (which could themselves also be compound propositions) connected by  , only if the significata of these propositions behave in the same way : If one of them is actually present (that is, if one of these propositions is true) the other is also present (that is, the other proposition is also true), and if one of these significata is not present (that is, if one of these propositions is false) the other is also not present (that is, the other proposition is also false).
, only if the significata of these propositions behave in the same way : If one of them is actually present (that is, if one of these propositions is true) the other is also present (that is, the other proposition is also true), and if one of these significata is not present (that is, if one of these propositions is false) the other is also not present (that is, the other proposition is also false).
The definition of negation as (negation figures in 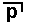 [that is, "not-p"], where p is a proposition), must read :
[that is, "not-p"], where p is a proposition), must read :
The significatum of the proposition p is not present
And from this the truth table of negation (as given in mathematical Logic) follows :

The entries in this table speak for themselves.
So now we have treated of all logical connectives in the propositional calculus and have interpreted them according to the tenets of intentional Logic. It turned out that when we define these connectives properly (that is, in accordance with intentional Logic) then the truth tables as given in mathematical Logic hold. And this means that we can use these tables for the derivation of the tautologies or theorems of the propositional calculus. However, in doing so, the propositional calculus is not a self-contained system anymore, but involves meaning, and meaning here implies things (states of affairs) which are signified by its propositions (single or compound) which in turn means that we go outside the system proper.
About the tautologies or theorems of the propositional calculus.
 where
where  is a double implication or equivalence, and p and q single propositions :
is a double implication or equivalence, and p and q single propositions :

(We have changed the order of the possible truth values of p and q in this table, which is of course totally immaterial.)
Here the compound propositions 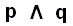 and
and 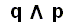 behave exactly in the same way with respect to the possible truth values of p and q, so they are equivalent :
behave exactly in the same way with respect to the possible truth values of p and q, so they are equivalent : 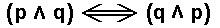 .
.
If we add in the truth table argument the truth table of  we get :
we get :
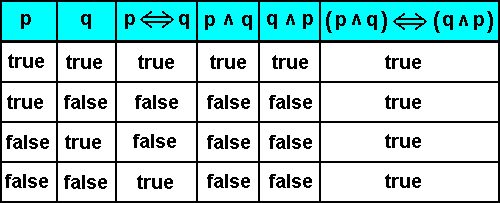
So here we clearly see that 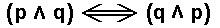 is always true no matter what the truth values of p and q are. Accordingly, we here have a logical law or tautology.
is always true no matter what the truth values of p and q are. Accordingly, we here have a logical law or tautology.
And here, because the tautology is about 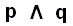 , that is, about
, that is, about 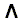 , it is also so acknowledged by intentional Logic, by reason of the fact that the truth-functional interpretation of
, it is also so acknowledged by intentional Logic, by reason of the fact that the truth-functional interpretation of 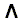 happens to give the same results as the intentional interpretation of
happens to give the same results as the intentional interpretation of 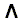 . That is, also for intentional Logic
. That is, also for intentional Logic 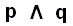 is only true when both p and q are true, and
is only true when both p and q are true, and 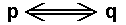 demands that p behaves in exactly the same way as q does, that is, when p is true, q must be true, and vice versa, and when p is false, q must also be false, and vice versa.
demands that p behaves in exactly the same way as q does, that is, when p is true, q must be true, and vice versa, and when p is false, q must also be false, and vice versa.
But we know that the case of implication is different : When ' implication ' is defined merely by its truth table (as the mathematical logicians do) it will not in all cases comply with this truth table as far as intentional Logic is concerned. As we saw earlier, sometimes nonsence is produced.
In the light of all this we will now show how to generally re-interpret the tautologies of the propositional calculus. We take as an example  .
.
According to respective truth tables we get :
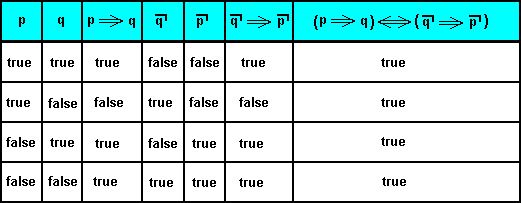
So, according to the truth-functional interpretation  is a tautology. It is always true no matter what the truth values of p and q are.
is a tautology. It is always true no matter what the truth values of p and q are.
Now we expound how such a tautology must be understood in the context of intentional Logic.
Clearly, in order for  to be true, it does not make any difference for what the proposition p stands, or for what q stands. Nor does it in a sense (about this sense, see immediately below) make any difference whether they be true or false.
to be true, it does not make any difference for what the proposition p stands, or for what q stands. Nor does it in a sense (about this sense, see immediately below) make any difference whether they be true or false.
The explanation of the tautological nature of our expression, an explanation, that is, which does not make use of truth tables, is as follows :
If we have non-q, then p cannot be implied by it, because then we would have q, because q is implied by p, therefore we have (when having not-q) not-p implied. And, the other way around : If we have p, then we cannot have not-q, because not-q implies not-p, therefore we must (when having p) have q. Here we see that we did not make use of the possible meanings of p and of q.
Yet, even though in such a formula we do abstract from the specific meanings of p and of q, we nonetheless recognize that there must be something in the meaning of such propositions that provides the foundation for the relation of implication between them (remember, p ==> q is the subject of the tautology in question). Consequently, in the propositional mold p ==> q, we do not mean just any proposition p, but rather any proposition whose meaning is such (this is the "in a sense" we spoke about above) that it implies another proposition. Similarly, q does not stand for any proposition, but rather any proposition of such a nature as to be implied by another.
Moreover, the important thing to notice is that in the proposition  taken as a whole, and which is a double implication,
taken as a whole, and which is a double implication,  , the antecedent of the-implication-going-to-the-right,
, the antecedent of the-implication-going-to-the-right,  , that is, all that lies at the left side of
, that is, all that lies at the left side of  , is not simply p, or the consequent, that is, all that lies at the right side of
, is not simply p, or the consequent, that is, all that lies at the right side of  , simply q, rather the antecedent is itself a conditional proposition, namely
, simply q, rather the antecedent is itself a conditional proposition, namely  , and the consequent likewise, viz.,
, and the consequent likewise, viz.,  . And precisely the same applies to the other direction of the double implication, namely
. And precisely the same applies to the other direction of the double implication, namely  .
.
So our tautology  is in fact two implications, namely
is in fact two implications, namely 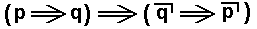 and
and 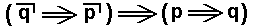 , and how to interpret the truth dependency of an implication along the lines of an intentional Logic was expounded above.
, and how to interpret the truth dependency of an implication along the lines of an intentional Logic was expounded above.
In other words, while the truth of the whole proposition is not dependent on the meaning of the propositions p and q, it is dependent on the meaning of  (when taking
(when taking  of the double implication), or is dependent on the meaning of
of the double implication), or is dependent on the meaning of  (when taking
(when taking  of the double implication). And because we do not specify the meanings of p and q, the s u b j e c t of the proposition
of the double implication). And because we do not specify the meanings of p and q, the s u b j e c t of the proposition 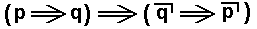 (that is, what the proposition is about) is now
(that is, what the proposition is about) is now  , that is implication itself, and the same is the case of the subject of
, that is implication itself, and the same is the case of the subject of 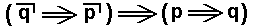 .
.
Read in either direction, the proposition  is not about the significata of its subject (term), but about the subject (term) itself, which here means about
is not about the significata of its subject (term), but about the subject (term) itself, which here means about  itself.
itself.
That is to say, it is in virtue of the nature and meaning of implication (as present in  and in
and in  ) that one is able to assert
) that one is able to assert  . In other words, the proposition is not about p and q just as such, but about the peculiarly logical relation of implication itself ( VEATCH, p.382/3 ). It is about
. In other words, the proposition is not about p and q just as such, but about the peculiarly logical relation of implication itself ( VEATCH, p.382/3 ). It is about  , respectively
, respectively  , to be sure, but, because p and q are not specified, it is about implication as such.
, to be sure, but, because p and q are not specified, it is about implication as such.
It is along these lines that the theorems or tautologies of the mathematical propositional calculus should be re-interpreted for an intentional Logic.
In order to demonstrate such adjudgements or re-interpretations to be made in the propositional calculus, let us first consider the proposition
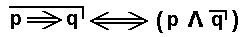
where  means the negation of that over which it is placed.
means the negation of that over which it is placed.
That this is a genuine equivalence is shown in mathematical Logic by means of truth tables :
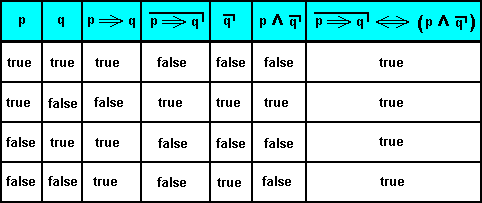
So indeed, according to the truth-functional interpretation 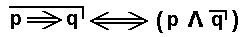 is a tautology, it is always true no matter what the truth values are of p and of q. The denial of the implication of q by p, is equivalent to the conjunction of p and not-q.
is a tautology, it is always true no matter what the truth values are of p and of q. The denial of the implication of q by p, is equivalent to the conjunction of p and not-q.
From this it follows -- still in the truth-functional context -- that denying such a conjunction implies the truth of the implication  :
:
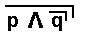

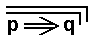

 .
.
However, we will find out that p ==> q is not obtained (as a meaningful proposition) in all cases (as it should, according to the truth tables) :
Suppose we (giving here an example as it is presented by VEATCH) let p signify the proposition
I am sitting at my desk,
and let q signify the proposition
New York is a large city.
Then 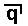 means : ' New York is not a large city '.
means : ' New York is not a large city '.
And now 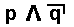 means :
means :
I am sitting at my desk and New York is not a large city.
And this (compound) proposition is obviously false.
So the compound proposition 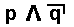 is false as soon as we consider the particular m e a n i n g s of p and q as they are given above, and, consequently, its negation
is false as soon as we consider the particular m e a n i n g s of p and q as they are given above, and, consequently, its negation 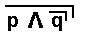 must be true. Therefore, because, according to the truth-functional interpretation, we have
must be true. Therefore, because, according to the truth-functional interpretation, we have 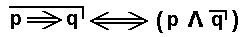 , we can say
, we can say
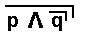

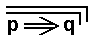

 .
.
If we assume that p is true (that is, we have p ), then we have :
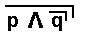

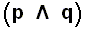 (which indeed is one of the possible outcomes resulting from negating the proposition
(which indeed is one of the possible outcomes resulting from negating the proposition 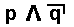 , and the only outcome when having p ). Accordingly (in our particular case at least) we have :
, and the only outcome when having p ). Accordingly (in our particular case at least) we have :
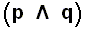

 .
.
So because what p and q signify can exist together ( I am sitting at my desk while New York is a large city ) we have  . But the latter compound proposition
. But the latter compound proposition  is nonsense, because it here means : ' If I am sitting at my desk, then New York is a large city '. And of course the size of the city of New York cannot in any way be dependent on whether I am sitting at my desk or not. That this is here nonsense, that is, that
is nonsense, because it here means : ' If I am sitting at my desk, then New York is a large city '. And of course the size of the city of New York cannot in any way be dependent on whether I am sitting at my desk or not. That this is here nonsense, that is, that  turns out to be nonsense, evidently is because the togetherness of p and q (the fact that I am sitting at my desk, and the fact that New York is a large city) is not imperative : They can be together, but need not be together : When I am not sitting at my desk, New York is still a large city. Indeed, the expression which we have arrived at, viz.,
turns out to be nonsense, evidently is because the togetherness of p and q (the fact that I am sitting at my desk, and the fact that New York is a large city) is not imperative : They can be together, but need not be together : When I am not sitting at my desk, New York is still a large city. Indeed, the expression which we have arrived at, viz., 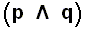

 , is also not possible according to the truth tables, because implication is certainly not equivalent to conjunction, as their respective truth tables show :
, is also not possible according to the truth tables, because implication is certainly not equivalent to conjunction, as their respective truth tables show :


So here we cannot simply rely on the truth-functional interpretation, because according to that interpretation we had 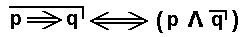 , being always true, no matter what p and q signify, and therefore also
, being always true, no matter what p and q signify, and therefore also 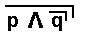

 , while we found out that in the above case
, while we found out that in the above case  turned out to be nonsense, while
turned out to be nonsense, while 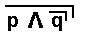 is perfectly possible in the form of
is perfectly possible in the form of 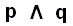 .
.
In all this we have seen, that as soon as we considered the meanings as were set above for p and q, the proposition 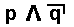 is definitely false, and thus its negation true, and, consequently, leading to the truth of
is definitely false, and thus its negation true, and, consequently, leading to the truth of  which, when interpreted according to those meanings of p and q, yields nonsense. This means that the falsity of
which, when interpreted according to those meanings of p and q, yields nonsense. This means that the falsity of 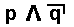 in fact turns out to imply, not the truth, but the falsity of
in fact turns out to imply, not the truth, but the falsity of  (because under the meanings set above for p and q the latter cannot be implied by the former) and thus not the falsity of
(because under the meanings set above for p and q the latter cannot be implied by the former) and thus not the falsity of 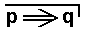 , which latter should be the case according to the equivalence of
, which latter should be the case according to the equivalence of 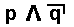 and
and 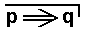 . So the truth table for this latter equivalence is violated in the present case. That is to say, the equivalence as established in the truth table cannot be true for all meanings of p and q, while it is true for all truth values of p and q. That is to say, it is not a tautology as soon as we involve meanings. If we leave out meanings alltogether, then it is a tautology. Indeed, in our example that state of affairs represented by the proposition p, viz., I am sitting at my desk, cannot in any way imply that state of affairs represented by the proposition q, viz., New York is a large city. So it is not their truth or falsity, but their meaning that is decisive for the equivalence
. So the truth table for this latter equivalence is violated in the present case. That is to say, the equivalence as established in the truth table cannot be true for all meanings of p and q, while it is true for all truth values of p and q. That is to say, it is not a tautology as soon as we involve meanings. If we leave out meanings alltogether, then it is a tautology. Indeed, in our example that state of affairs represented by the proposition p, viz., I am sitting at my desk, cannot in any way imply that state of affairs represented by the proposition q, viz., New York is a large city. So it is not their truth or falsity, but their meaning that is decisive for the equivalence 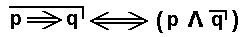 to be true, that is, for it to be a genuine equivalence.
to be true, that is, for it to be a genuine equivalence.
On the other hand, there are cases where the implication is not nonsense at all, but absolutely necessary, so that in these cases the truth table method happens to work well :
Consider the following negation of a conjunctive compound :
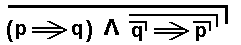
In line with 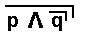

 , which itself derives from the following truth table :
, which itself derives from the following truth table :
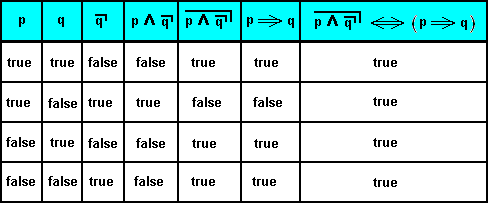
we can say :

Is this latter implication, viz., 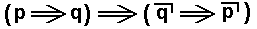 always true? Yes it is. It can syllogistically be proved ( here, ==> can legitimately be identified with "is", because "is" is at least equivalent to ==> ) :
always true? Yes it is. It can syllogistically be proved ( here, ==> can legitimately be identified with "is", because "is" is at least equivalent to ==> ) :

We can also prove the case where the central implication goes to the left (having then proved the equivalence of p ==> q and not-q ==> not-p ) :
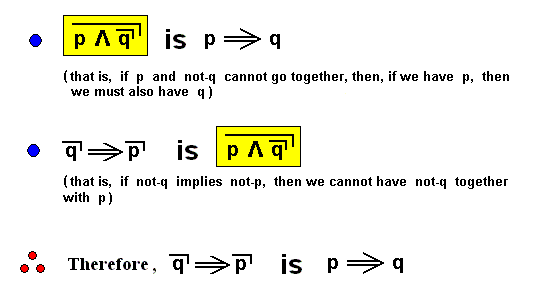
So we have proven (not by means of truth tables) that the proposition  is always true no matter what the propositions p and q s i g n i f y, and then, of course also
is always true no matter what the propositions p and q s i g n i f y, and then, of course also 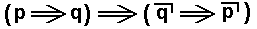 , that is, the implication.
, that is, the implication.
( this, in contrast to the previous example where the corresponding implication was simply  , which indeed cannot as such be proved true [because there are different propositions on either side of ==> , whereas in ( p ==> q ) ==> (not-q ==> not-p) we have the same propositions on either side of the (central) ==> ] ).
, which indeed cannot as such be proved true [because there are different propositions on either side of ==> , whereas in ( p ==> q ) ==> (not-q ==> not-p) we have the same propositions on either side of the (central) ==> ] ).
And because of this our proposition

has not yielded nonsense. The negation of a conjunction here resulted in an implication that is always true.
Because we now know that  is always true,
is always true,  can never go with its opposite, which here also means it can never go with the negation of
can never go with its opposite, which here also means it can never go with the negation of  , that is, the conjunction
, that is, the conjunction 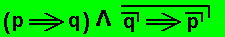 is impossible in principle (i.e., not just in a particular case), therefore its negation
is impossible in principle (i.e., not just in a particular case), therefore its negation  is true and so its equivalent
is true and so its equivalent 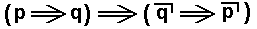 .
.
In fact, the difference between the first example, which was about  , and the second example, which was about
, and the second example, which was about 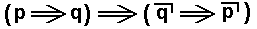 , is that, on the one hand, the compound proposition
, is that, on the one hand, the compound proposition  is about objects of first intention, that is, it is about the state of affairs that is signified by the proposition p (signified in extramental reality, or in a reality considered as if it were extramental) (and it asserts that another state of affairs, signified by the proposition q, is implied), while, on the other hand, the compound proposition
is about objects of first intention, that is, it is about the state of affairs that is signified by the proposition p (signified in extramental reality, or in a reality considered as if it were extramental) (and it asserts that another state of affairs, signified by the proposition q, is implied), while, on the other hand, the compound proposition 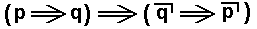 is about the proposition p ==> q as such, that is, as (compound) proposition and thus as logical intention (it asserts that this proposition [as proposition] implies the proposition not-q ==> not-p [as proposition] ), i.e., it is about objects taken in second intention. This is evident from the fact that -- in contrast to the first implication -- we here have on either side of the central implication the same propositions, namely p and q at the left side, and p and q at the right side.
is about the proposition p ==> q as such, that is, as (compound) proposition and thus as logical intention (it asserts that this proposition [as proposition] implies the proposition not-q ==> not-p [as proposition] ), i.e., it is about objects taken in second intention. This is evident from the fact that -- in contrast to the first implication -- we here have on either side of the central implication the same propositions, namely p and q at the left side, and p and q at the right side.
In short, when we interpret things in line with intentional Logic, there would seem to be a marked difference between what might be called
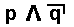 can be denied, yielding
can be denied, yielding  , which, however turned out to be nonsense, and therefore not complying with the truth-functional interpretation,
, which, however turned out to be nonsense, and therefore not complying with the truth-functional interpretation,
Intentional Logic thus wants there to be a distinction between
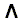 ,
,
 ,
, 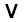 . As such
. As such 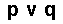 means : either p, or q, but not both of them together.
means : either p, or q, but not both of them together.
Does the propositional calculus upset the claim of the syllogism to be the exclusive instrument of deductive demonstration?
VEATCH, p.384, quotes the mathematical logician TARSKI :
Almost all reasonings in any scientific domain are based explicitly or implicitly upon laws of the sentential calculus.Where "sentential calculus" means propositional calculus. And in fact these laws (that is, the tautologies or theorems of the propositional calculus) are regarded as being simply so many "validating forms of inference".
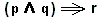 ], its truth depends on the truth of the component propositions, while the truth of tautologies is not so dependent ) -- is not the exclusive instrument of deductive demonstration or inference.
], its truth depends on the truth of the component propositions, while the truth of tautologies is not so dependent ) -- is not the exclusive instrument of deductive demonstration or inference.
The following truth table shows that the syllogism ( 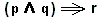 ) is indeed not a tautology, that is, it is not true for all possible truth values of its component propositions ( p, q, r ) :
) is indeed not a tautology, that is, it is not true for all possible truth values of its component propositions ( p, q, r ) :
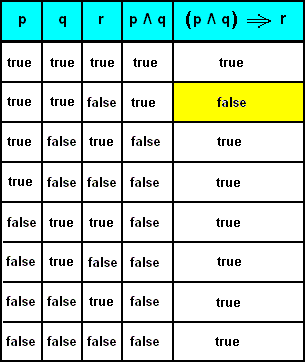
In intentional Logic both premises (p and q) must be true in order for the conclusion (r) to be true. And only when this is the case (first entry of the table) the implication as such, namely
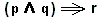 , is true. According to intentional Logic, all other truth-false configurations result in the falsity of the implication.
, is true. According to intentional Logic, all other truth-false configurations result in the falsity of the implication.On the other hand, the modus ponens inference : If q is implied by p, and if we have p, then we have q, is as such a tautology :

The inference 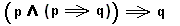 is true for all truth values of the component propositions p and q. This is so by reason of the fact that at the right side of the main implication no new proposition is produced.
is true for all truth values of the component propositions p and q. This is so by reason of the fact that at the right side of the main implication no new proposition is produced.
How has it come to be that way, that is, why is there, apparently, no new proposition produced? Well, it appears so because the modus ponens is in fact an abbreviation of a larger structure. That is, something is omissed. Indeed, in order to be able to assert the modus ponens' major premise ( p ==> q ) something must be presupposed, that is, something that is not explicitly mentioned in this premise and in the whole modus ponens inference for that matter. And, as has already been shown earlier, when we add this presupposition explicitly to the modus ponens structure, we obtain a genuine syllogism.
Let us show this once more by means of an example.
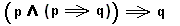 which is a tautology.
which is a tautology.
p = x is a crystal.
q = x is periodic.
Our modus ponens inference then becomes :
e = all crystals are periodic.
p = x is a crystal.
q = x is periodic.
And the syllogism can now be written as one compound proposition 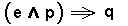 . And here we clearly see that a different proposition is implied by the propositions e and p, like it was above with the syllogism
. And here we clearly see that a different proposition is implied by the propositions e and p, like it was above with the syllogism 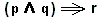 , which means that it also cannot be a tautology.
, which means that it also cannot be a tautology.
So indeed, if we fully write out the modus ponens inference we get a genuine syllogism. Therefeore, the modus ponens inference is just an incomplete syllogism, implying that, when properly conceived, it is not a tautology.
The theorems (tautologies) of the propositional calculus contain connectives (connecting component propositions) such as
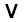 ,
, 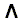 ,
,  and
and  . But their main or major connective is always either
. But their main or major connective is always either  (implication) or
(implication) or  (double implication, equivalence).
(double implication, equivalence). is just a double implication, it is sufficient for us to focus on
is just a double implication, it is sufficient for us to focus on  , that is, on implication.
, that is, on implication.Consider the following two implicative (and conditional) (compound) propositions :
p signifies the proposition ' x is a towel '.
q signifies the proposition ' x is capillary '.
r signifies the proposition ' x is absorbent '.
Now the two compound propositions can be translated into the language of the propositional calculus :
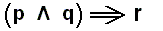
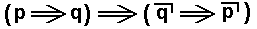
 (as one way of expressing), if we have
(as one way of expressing), if we have 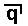 we cannot have p (because p implies q ), so then we must have
we cannot have p (because p implies q ), so then we must have 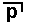 , that is,
, that is,  (second way of expressing).
(second way of expressing). signifies), but about
signifies), but about  itself, that is, about the proposition
itself, that is, about the proposition  as proposition.
as proposition. .
. , when we have p, we cannot have
, when we have p, we cannot have 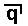 , because then we would have
, because then we would have 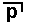 in stead of p, and thus, when we have p, we must have q, that is,
in stead of p, and thus, when we have p, we must have q, that is,  .
. . And also according to the truth table method this is so, as we found out earlier . Accordingly, this tautology says that
. And also according to the truth table method this is so, as we found out earlier . Accordingly, this tautology says that  expresses the same thing as is expressed by
expresses the same thing as is expressed by  .
.
An implication (such as
 , or more complex ones such as
, or more complex ones such as 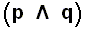

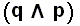 , or
, or 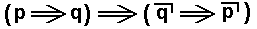 ) is, as we know, an enthymeme, that is, it is in fact an abbreviated syllogism, in this case a categorical syllogism provided with an uncertainty clause. Accordingly, an implication ultimately involves the relation of identity.
) is, as we know, an enthymeme, that is, it is in fact an abbreviated syllogism, in this case a categorical syllogism provided with an uncertainty clause. Accordingly, an implication ultimately involves the relation of identity. , is "is", and so also involves the relation of identity.
, is "is", and so also involves the relation of identity. or by
or by  ) are genuine logical intentions, and this in turn means that all theorems (tautologies) of the propositional calculus are logical intentions.
) are genuine logical intentions, and this in turn means that all theorems (tautologies) of the propositional calculus are logical intentions.
Returning to our above example  , what this theorem is about is a particular propositional relation called "implication" and symbolized by
, what this theorem is about is a particular propositional relation called "implication" and symbolized by  . In fact the theorem really expresses a property of that second intentional being called "implication" (here figuring in
. In fact the theorem really expresses a property of that second intentional being called "implication" (here figuring in  , or, if we read backwards, figuring in
, or, if we read backwards, figuring in  ). In other words, it is only in virtue of the nature, not of a real being, but rather of a being of reason (that is either the proposition
). In other words, it is only in virtue of the nature, not of a real being, but rather of a being of reason (that is either the proposition  or the proposition
or the proposition  ), that the consequent follows (reading forward or backward) in this particular theorem. The implication (in
), that the consequent follows (reading forward or backward) in this particular theorem. The implication (in  or in
or in  ) here intends a 'causal' pattern (in the present case it is of course not really causal, because time is not involved here) in mere logical entities or beings of reason. That is to say, in this case it is because of the nature of implication (a being of reason or object of second intention) that
) here intends a 'causal' pattern (in the present case it is of course not really causal, because time is not involved here) in mere logical entities or beings of reason. That is to say, in this case it is because of the nature of implication (a being of reason or object of second intention) that  follows, as a property of implication, from
follows, as a property of implication, from  , or, also, that
, or, also, that  follows, as a property of implication, from
follows, as a property of implication, from  .
.
If implication always signifies or intends a certain causal order or pattern, and if the intention of causal order always involves a syllogistic ordering of the intending propositions, then presumably it should make no difference whether the intention of the implication be aimed at a causal order among objects of first intention or at a 'causal' order among objects of second intention -- in either case the implicative connection between the intending propositions (major premise, minor premise, conclusion) should be syllogistic in character. And so in fact it would seem to be in the case of the major implicative and double implicative connections that appear in the various theorems of the propositional calculus. Why is it, one might ask, that  is but another way of expressing the same truth expressed by
is but another way of expressing the same truth expressed by  ? The answer is that it is but another way of expressing
? The answer is that it is but another way of expressing 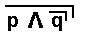 , and that
, and that 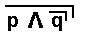 is but another way of expressing
is but another way of expressing  :
:
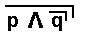

 .
.


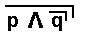 .
.


 .
.
Where
 = is.
= is.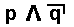 must be a denial in principle, and not just in fact.
must be a denial in principle, and not just in fact.
REMARK :
 ) also in accidental propositions such as in ' Socrates is tanned ', that is, we also here can say ' Socrates <==> tanned '. This as a result of the identical designation of the subject term ( ' Socrates ' ) and the predicate term ( ' tanned ' ). Accordingly, the above derivation is a genuine syllogism.
) also in accidental propositions such as in ' Socrates is tanned ', that is, we also here can say ' Socrates <==> tanned '. This as a result of the identical designation of the subject term ( ' Socrates ' ) and the predicate term ( ' tanned ' ). Accordingly, the above derivation is a genuine syllogism.
All this can also be argued from a more general position. As is well known, the mathematical logicians have been careful to distinguish between the theorems or (what they call) validating forms of inference within the propositional calculus itself and the rules of proof or derivation by means of which these theorems or validating forms are themselves demonstrated or derived. Of these so-called rules of proof the principal ones are the modus ponens rule and the rule of substitution.
Thus, as regards the rule of substitition, it would seem to turn on nothing other than the principle of the dictum de omni et nullo.
This is the principle as regards every subaltern (de omni) and as regards no subaltern (de nullo).
The principle of de omni reads :
All what is attributed to a given subject taken in its dividing generality, must also be attributed to all its subalterns.
For example :
The principle of de nullo reads :
Both arguments are syllogistic and go from general to special, that is, the special (i.e., the subaltern) substitutes the general.
Substitution also occurs where the definiens is substituted for the definiendum :
Here the definiens (that is, the definition proper) ' rational animal ' is substituted by its definiendum (i.e., that what must be defined) ' human being '.
As regards the modus ponens rule, we have already shown above that it is in fact a syllogism as soon as we contemplate the modus ponens in its full extent.
So indeed these two rules of proof, substitution and modus ponens, both involve the structure of the syllogism and therefore the rules of the syllogism.
Theorems that are improper and irrelevant to the propositional calculus.
If all the above is sound, and if the theorems of the propositional calculus are to be understood as mere forms of immediate inference (that is, an inference drawn from the antecedent (complex) term as term), then it will turn out that some few of the theorems that have customarily been included in the calculus do not really belong there at all.
An example is :

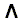



Here we cannot say that  is just another way of expressing
is just another way of expressing 
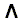
 , because
, because  is, it is true, contained in (of course)
is, it is true, contained in (of course)  as well as in
as well as in 
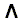
 , but
, but  is not contained in
is not contained in  , and also
, and also  is not contained in
is not contained in  .
.
So such theorems, although being tautological, do not belong in the propositional calculus.
So far our discussions and explanations concerning argument in Logic.
This concludes our exposition of INTENTIONAL LOGIC as first proposed by VEATCH, 1952 (1970), and presented on this website in Part I -- VII.
Despite its soundness it of course still does not settle once and for all the issue whether mathematics and especially mathematical Logic is or is not the proper instrument of science, as is commonly believed.
As far as I can see, mathematics, and also mathematical Logic (as a part of mathematics) deals with all possible relational patterns. Many such patterns can figure as models of physical processes insofar their mathematical aspect is concerned. Mathematical patterns can be intended by concepts, subject-predicate propositions, and syllogistic arguments, and also real patterns in extramental reality can be so intended.
As regards a model in physical science, the model can be intended by a syllogism or series of syllogisms, and the model itself is an instrumental sign for some pattern in extramental reality. But the expression "is an instrumental sign for some pattern in extramental reality " must be taken with caution : While a genuine logical intention or formal sign is about something, implying it to be on a different logical level from that of the thing intended, the instrumental sign is only per accidens about something else, and resides therefore at the same logical level as that of the thing to which it is supposed to point.
A model pretends to be an approximation to genuine knowledge of the physical, while many aspects of the latter can be directly intended, that is, without instrumental signs, for example in observations of aspects of extramental reality.
Mathematics, and also mathematical Logic (which is a part of mathematics dealing with the truth function) is a methodological tool for the execution of natural science. It is not a logical tool. The fact that (1) in all mathematical systems that are qua complexity above the Peano Arithmetic (and above finite Groups I assume), and (2) in all systems of mathematical Logic that are qua complexity above the propositional calculus, the 'Gödel phenomenon' occurs, could perhaps have to do with the fact that these systems are non-intentional. That is, as soon as such a non-intentional system reaches a certain degree of complexity, it starts, so to say, to break apart, and defies provable consistency.
In the next documents we will develop a metapyhysics, or better, an ontology, that is broader than just aristotelian metaphysics, that is, a metaphysics that, in a way, contains aristotelian metaphysics as a constituent.
Outlook and further study.
With the present document we have come to a temporary end of our exposition of Aristotelian metaphysics (theory of natures) and its associated logic (intentional logic). The documents to follow will more and more concentrate on the evolution of organisms especially in placing it in a broad metaphysical context. For this, the ideas about the Explicate and Implicate Orders are further worked out, but still with the Aristotelian theory of natures in mind. This has taken a long time. And we have thought it to be important not only to speak about "organic evolution" as such, but to actually be in the middle of it. For this we chose insects and their evolution, because this is the largest and most diverse animal group, known already from Carboniferous times onwards. While acquainting ourselves with the many special features encountered in the evolution of these organisms, we were able to test and work out further the overall metaphysical context of evolution, and of all natural things for that matter. We did this already in the present (Fifth) Part of Website, but continued it in Sixth Part of Website. Especially there, we developed our "noëtic theory of organic evolution" which has yielded much about the supposed structure and nature of the Implicate Order (See directly after part VIII [Sixth Part of Website] ). And at the end of Sixth Part of Website, from part XV onwards, we returned all out to Aristotelian metaphysics, but now placing it into our theory of the Explicate / Implicate Order. The latter theory expounds the distribution of features inherent in aristotelian metaphysics -- such as intensive qualities, and substances seen as holistic enties -- over the two reality-domains, the Explicate Order and the Implicate Order. It boils down to especially studying features such as extensionality, spatial continuity, intensionality, quality, quantity, place, space, motion, time, and inorganic substances (in the metaphysical sense) such as atoms, molecules, and crystals. This is, what one may call the (aristotelian) "philosophy of nature"
And, of course, if the reader wants to continue the quest for aristotelian metaphysics (as begun with in present Part of Website), he or she may skip all what is coming next (i.e. all about biological and noëtic evolution), and directly continue with part XV in Sixth Part of Website.
Subsequent to the (aristotelian) "philosophy of nature" as expounded in that part XV, and in XVa (Sixth Part of Website), will come the aristotelian doctrine of "being qua being", which is his ultimate metaphysics of Being (and which we accept almost fully). As was indicated in the " Theory of Natures" part I in present Part of Website, this metaphysics is best explained by J. Owens, in his " The Doctrine of Being in the Aristotelian Metaphysics". Before continuing with the mentioned parts XV and XVa in Sixth Part of Website, the reader should again study the document " Theory of Natures" part I, in present Part of Website.
But, of course, if the reader wants directly to delve into the realm of organic evolution and its help in setting up an extended metaphysics, i.e. aristotelian metaphysics extended with the theory of the Explicate / Implicate Orders, he or she may continue with the next documents to come in present and next Part of Website.
e-mail :
 ( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
( Please write in ' Subject ' entry : ' METAPHYSICS ', in order for me to be able to distinguish your mail from spam )
To continue click HERE for study of the deterministic structure of the World, Part I.
Back to Aristotelian metaphysics Part I
Back to Aristotelian metaphysics Part II
Back to Aristotelian metaphysics Part III
Back to Aristotelian metaphysics Part IIIa
Back to Aristotelian metaphysics Part IV
Back to Aristotelian metaphysics Part V