2-D patterns XX

The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part XX (Subgroups and Antisymmetry in Ornaments)

e-mail :

Sequel to Group Theory

As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Infinite two-dimensional periodic patterns, or Ornaments (sequel)

In the previous document we investigated antisymmetry patterns derivable from a P2gg pattern.
As initial P2gg pattern we had chosen the pattern of Figure 9 of Part XVII of the present Series. Here we will continue this investigation, before going on to other plane groups, and reproduce the chosen intial P2gg pattern just mentioned.

Figure 1. Pattern representing plane group P2gg . In previous as well as in the present document it is chosen as initial pattern from which antisymmetry patterns are derived. The background color of the motifs s.str. (commas) is set to be blue, representing the initial color. The area representing the identity element is indicated by the symbol 1 .

Figure 2. P2gg pattern of Figure 1, with the two generating glide lines (dashed lines) and the generating half-turn (rotation by 180⁰) (small red solid ellipse) indicated. While the small red ellipse indicates the symmetry element of the half-turn (namely the [location of the] two-fold rotation axis), the area of the pattern marked h represents the group element which is a half-turn about the axis indicated.

An antisymmetry pattern can be derived from the above given initial P2gg pattern by replacing the generating half-turn h by the antisymmetry half-turn e₁h , where the antiidentity transformation is again interpreted as the color permutation (Blue Red) (cycle notation) with respect to the background color.
As we did before, we derive the antisymmetry pattern in several steps, indicating the newly generated red elements for the time being with the color purple, and the newly generated blue elements with the color green. The purple and green colors will later be restored to red and blue respectively.
Recall that e₁h = he₁ , and that (e₁)² = 1 (which is the identity element), h² = 1 , and (e₁h)² = e₁he₁h = he₁e₁h = h² = 1 .

Figure 3. From the identity element (which has the initial color blue [here indicated by green] ) a red (purple) element -- the element e₁h -- is generated by applying the antisymmetry half-turn ( The symmetry element of which is indicated by a small blue solid ellipse).

Figure 4. From the two elements 1 and e₁h new elements are generated by subjecting them to the generating translations, and the results again to those translations.

Figure 5. From the identity element another blue (here indicated by yellow) element is generated by one time applying the generating vertical glide reflection in the upward direction.
From this new element other blue (green) elements are generated by the vertical and horizontal translations. The two generating glide reflections (g) are indicated.

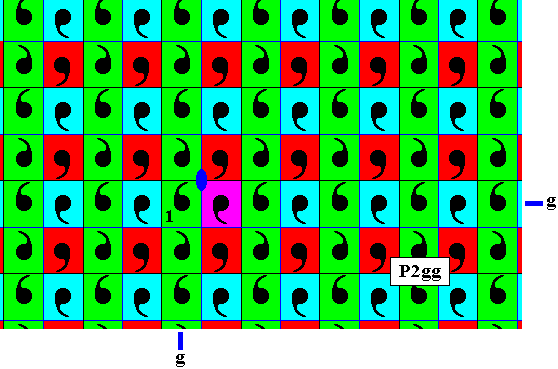
Figure 6. From the blue (green) element directly above the identity element a new element is generated, by applying to it the antisymmetry half-turn, that must change color with respect to that blue (green) element (just above the identity element), so its color will be red (purple).

Figure 7. The pattern is completed by applying translations.

Restoring green to blue and purple to red results in the definitive antisymmetry pattern :

Figure 8. Definitive antisymmetry pattern derived from the generating pattern of Figure 1 by replacing the generating half-turn (blue solid ellipse) by its corresponding antisymmetry transformation (antisymmetry half-turn).

The antisymmetry pattern just obtained is identical to one obtained earlier (See Figure 15 of Part XVII of the present Series ) by replacing the generating horizontal glide reflection by its corresponding antisymmetry transformation.
This was to be expected, because the half-turn (of the generating pattern) is implied by the other symmetries of the pattern.

The pattern of blue elements of the just derived antisymmetry pattern can be generated by subjecting the identity element to the generating vertical glide reflection (which is an element of the full (P2gg) group, yielding the whole column of blue elements containing the identity element, and then subjecting this column to repeated horizontal translation (which is also an element of the full group). So this pattern of blue elements is a subgroup, and its symmetry is according to the plane group Pg (because the horizontal glide reflections and the half-turns are destroyed, resulting in the only symmetries of this pattern to be the horizontal and vertical translations and one type (namely vertical) of glide reflection).
The symbol for the just derived antisymmetry pattern must accordingly read P2gg / Pg .

The next Figures check whether indeed the generating half-turn about the axis indicated involves color change (in virtue of it being replaced by the corresponding antisymmetry half-turn e₁h ).

Figure 8.

Figure 9.

Figure 10.

Figure 11.

Figure 12.

I do possess only one example of an antisymmetry pattern found in Neolithic art mathematically derivable from a corresponding generating P2gg symmetry pattern.

JABLAN, S., 2002, Symmetry, Ornament and Modularity, p. 145 gives two alleged examples (Fig. 2.108 (e) and (f)), but one of them (e) is not really an antisymmetry pattern derived from a P2gg pattern, but can be derived from a C2mm symmetry pattern (JABLAN uses the short notation pgg for the group P2gg as we denote it).

Figure 13. Generating P2gg pattern from which an antisymmetry pattern found in Neolithic art can be derived by replacing the horizontal generating glide reflection by its corresponding antisymmetry transformation.

Before deriving the antisymmetry pattern we will first analyze the just given generating P2gg pattern.

Figure 14. Unit mesh of the generating P2gg pattern.

Figure 15. Illustration of the equivalence of the four corner points of the unit mesh of the generating P2gg pattern.

Figure 16. Point lattice (indicated by blue connection lines) of the generating P2gg pattern.

Figure 17. Blow-up of a part of the above given generating P2gg pattern. The red triangles of the pattern are mirror symmetric to the blue triangles (Colors do not signify (anti)symmetry features). See next Figure.

Figure 18. A horizontal glide line (indicated by a solid blue line) of the above generating P2gg pattern.

Figure 19. Illustration of the horizontal glide reflection of the above given generating P2gg pattern.
a is reflected in the glide line (resulting in b) and then shifted along it, resulting in c . Stage b is only intermediary and as such not belonging to the result of the transformation, i.e. a is transformed into c .

On the basis of the foregoing we now know where exactly the horizontal glide lines of our generating P2gg pattern lie. One of them we choose as generating horizontal glide line :

Figure 20. Generating horizontal glide reflection line of the above (Figure 13 ) given generating P2gg pattern.

Figure 21. Illustration of the action of the generating horizontal glide reflection line (glide reflection) g_h of the above (Figure 13 ) given generating P2gg pattern. Colors do not signify symmetry features.

Figure 22. Illustration of the action of a vertical glide reflection line of the above (Figure 13 ) given generating P2gg pattern. We choose this one as to be the generating vertical glide reflection g_v . The generating horizontal glide reflection line is also indicated. Colors do not signify symmetry features.

From the above initial pattern (generating symmetry pattern) we can derive an antisymmetry pattern by replacing the horizontal generating glide reflection g_h by its corresponding antisymmetry transformation e₁g_h , where the antiidentity transformation e₁ stands for the color permutation (Blue Red) (cycle notation). We will set the color blue as the original color. An odd number of e₁'s (which reduces to one e₁ ) in the symbol of a given group element will change the color of the area that represents this group element from blue to red.
To clarify the derivation we begin by showing the resulting color alternations in one row only. For this we can use Figure 21, where we, however, now interpret g_h as being e₁g_h . This Figure shows the color alternation along the glide line by means of the colors red and blue.
In the next Figure we subject a red element lying on the vertical glide line repeatedly to the vertical glide reflection, resulting in a series of red elements (all red because the vertical glide reflection is not an antisymmetry transformation). Then we do the same with a blue element lying on the vertical glide line. This results in :

Figure 22a. Action of the (repeated) vertical glide reflection performed on a red and on a blue element. This vertical glide reflection does not effect color change.

When we now apply (repeatedly) the horizontal translation (which is not an antisymmetry transformation) to the elements already generated, we get the whole antisymmetry pattern. Some beginnings of this process are indicated in the next Figure.

Figure 22b. Illustration of the repeated application of the horizontal translation to the elements already generated earlier.

On the basis of the above we can now give the whole antisymmetry pattern, and after this we give that same antisymmetry pattern in black and white, as it is known from Neolithic art (or as it is depicted in the literature, here in JABLAN, S., 2002).

Figure 23. Antisymmetry pattern (with color alternation Blue -- Red) derived from the generating P2gg pattern of Figure 13 by replacing the generating horizontal glide reflection g_h by the horizontal antisymmetry glide reflection e₁g_h .
This result should be compared with an earlier derivation of this same antisymmetry group (i.e. a derivation involving the same replacement of symmetry transformations by antisymmetry transformations) from a simpler version of the initial P2gg pattern : Figure 15 of Part XVII of the present Series.

Figure 24. A unit mesh of the just derived antisymmetry pattern is indicated.
Its dimensions are the same as that of the generating P2gg pattern (Figure 14 ).

Figure 25. Four unit meshes of the just derived antisymmetry pattern are indicated to show the point lattice.

The next Figure shows the isolated set of blue elements (where we considered blue to be the initial color, and where we consider this set to contain the identity element).

Figure 26. Subpattern of the above derived antisymmetry pattern. This subpattern consists of all the blue elements of the antisymmetry pattern, and is supposed to contain the identity element.

Figure 27. Illustration of the vertical glide line of the subpattern of the above derived antisymmetry pattern.

It is clear that the subpattern of blue elements is periodic, and that its only symmetries are horizontal and vertical translations and vertical glide lines, so its symmetry is that of the plane group Pg . And because the pattern can be generated from the area representing the identity element of the generating P2gg pattern and of the antisymmetry pattern, by applying to it the generating vertical and horizontal translations and the generating vertical glide reflection, which are all elements of the full groups (generating group and antisymmetry group), the pattern of blue areas represents a genuine subgroup of the two mentioned full groups. Consequently the symbol of the antisymmetry group must read : P2gg / Pg .

The next Figure gives the same antisymmetry pattern as was just derived, but now instead of the colors blue and red the colors black and white, as it occurs in Neolithic art.

Figure 28. Antisymmetry pattern P2gg / Pg derived from the generating P2gg pattern of Figure 13.
After JABLAN, 2002

Subgroups

We will now discuss some s u b g r o u p s of the plane group P2gg not necessarily associated with antisymmetry or color symmetry. These subgroups are indicated by the color yellow.

Figure 29. Subgroup C₂ (which is a rosette) of the full group P2gg (Figure 1 ), generated by the half-turn about the axis indicated.

Figure 30. Subgroup p1g (which is a frieze pattern isomorphic to C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating vertical glide reflection.

Figure 31. Subgroup p1g (which is a frieze pattern isomorphic to C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating horizontal glide reflection.

Figure 32. Subgroup p11 (which is a frieze pattern isomorphic to C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating horizontal translation.

Figure 33. Subgroup p11 (which is a frieze pattern isomorphic to C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating vertical translation.

Figure 34. Subgroup P1 (which is a plane pattern isomorphic to C_infinity x C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating vertical and horizontal translations.

Figure 35. Subgroup Pg (which is a plane pattern isomorphic to C_infinity x C_infinity ) of the full group P2gg (Figure 1 ), generated by the generating vertical glide reflection and the horizontal translation.

Figure 36. Illustration of the action of the vertical glide line which together with the horizontal translation generates the subgroup Pg of the previous Figure.

Figure 37. Subgroup P2gg (which is a plane pattern isomorphic to C_infinity x C_infinity ) of the full group P2gg (Figure 1 ), generated by the transformations (g_h)³ and (g_v)³ (which are also elements of the full group).
The generating half-turn (its symmetry element, i.e. its axis, indicated by the red solid ellipse) of the full group is not an element of this subgroup. On the other hand, the half-turn, of which the corresponding symmetry element (axis) is indicated by a blue solid ellipse, is an element of the subgroup, and it can be choosen as one of the generators of the full group.

The next Figure shows that the half-turn (indicated by the blue solid ellipse) -- which is an element of the subgroup -- is also an element of the full group (parent group), namely the element (g_v)³(g_h)^-3 , as it should be.

Figure 37a. Subgroup P2gg of the previous Figure. The half-turn indicated by its symmetry element (rotation axis), a blue solid ellipse, is an element of this subgroup, and also an element of the parent group, because it is equivalent to the element (g_v)³(g_h)^-3 , which clearly is an element of the parent group.

The next Figure gives yet another subgroup also having P2gg symmetry.

Figure 38. Subgroup P2gg (which is a plane pattern isomorphic to C_infinity x C_infinity ) of the full group P2gg (Figure 1 ), generated by the transformations g_h and (g_v)³ (which are also elements of the full group).
This subgroup is called H in the discussion below.

Figure 39. Illustration of the transformation (g_v)³ as it is combined with the elements generated (from the identity element) by the transformation g_h .

The next Figure extends the pattern as depicted in Figure 38 in order to clearly let stand out the symmetry content of the subgroup.

Figure 39a. Extension of the pattern of Figure 38, representing the P2gg parent group and the P2gg subgroup. In the next Figure this subgroup is isolated.

Figure 39b. The subgroup P2gg of the above Figures isolated.
One can clearly see that its symmetries consist of horizontal and vertical glide reflections, horizontal and vertical translations and half-turns. So its symmetry is that of the plane group P2gg , and has, consequently, the same symmetry as its parent pattern.

The just derived subgroup pattern P2gg of the parent group pattern P2gg consists of rows. Which rows? Well every third row of the parent pattern. It has the symmetry of the plane group P2gg (the same as the parent pattern) because it can be generated by repeatedly applying two glide reflections, the glide lines of which are perpendicular to each other.
The row of elements containing the generating horizontal glide line (and thus containing the identity element) is a subgroup (p1g) of the present subgroup and also of the parent pattern. It was depicted in Figure 31.
Let us call the subgroup with P2gg symmetry (consisting of horizontal rows of elements, as it was established in Figure 38 and Figure 39b ) the subgroup H . These rows -- apart from the row containing the generating horizontal glide line, i.e. (apart from) the row generated by the generating horizontal glide relection -- are left cosets of the just mentioned row containing the generating glide line (which row is a subgroup), by the elements (g_v)^3k , where k is an element of the set of integers. They form a decomposition of our subgroup P2gg , which we called H .
Let us now determine the left and right cosets of H by an element not in H , such as g_v , which means that we multiply that element with all the elements of H in both directions, i.e. we form the left coset g_vH and the right coset Hg_v .

The next Figure shows the area (originally belonging to the parent pattern) representing the just mentioned element g_v .

Figure 39c. The subgroup H .
The area (green) representing the element g_v is indicated. This element is not an element of the subgroup, but it is an element of the parent pattern (i.e. the full P2gg group).

For c o s e t s see Part V of the general Series on Group Theory. To see this Part in a separate window click HERE , and after consulting it close the window to return to the present document.
For the concept of n o r m a l s u b g r o u p , see towards the end of Part XV of that same Series. To see this Part in a separate window click HERE , and after consulting it close the window to return to the present document.
The short discussion on cosets and normal subgroup below (in the present document) is a little of a diversion not essential for understanding the topics presently at issue.

Let us first derive the left coset g_vH of the subgroup H by the element g_v (generating vertical glide reflection), which means that we first take an element of H and then apply to it the element g_v . This we do for every element of H (i.e. for every yellow element in every row). The next Figure shows this for some elements of the subgroup, before giving the final result.

Figure 39d. The subgroup H (yellow) of the full group (yellow + blue).
Generation of the left coset of H by the element g_v , illustrated for some elements of H .
From the element a of H the element b (as an element of the left coset of H by the element g_v ) is generated.
From the element c of H the element d (as an element of the left coset of H by the element g_v ) is generated.
From the element e of H the element f (as an element of the left coset of H by the element g_v ) is generated.
From the element g of H the element h (as an element of the left coset of H by the element g_v ) is generated.
From the element i of H the element j (as an element of the left coset of H by the element g_v ) is generated.
From the element k of H the element m (as an element of the left coset of H by the element g_v ) is generated.

If we do this with all the elements of the subgroup H we will obtain its left coset by the element g_v . See next Figure.

Figure 40. Left coset (purple colored rows representing (rows of) group elements) of the subgroup P2gg (yellow), which is here called H .
All elements of this coset lie in the rows immediately above the rows of H .

Now we're going to determine the right coset Hg_v of the subgroup H also by the element g_v , which means that we now first take the element g_v , and then apply to it every element of the subgroup H (Recall that a group element of a symmetry group is always a symmetry transformation, i.e. a transformation which leaves the pattern unchanged in appearance).
To begin with we apply all the elements of the row containing the generating horizontal glide line successively to the element g_v . We first show this for a few elements of this row, before giving the final result (but still regarding (only) the row containing the horizontal generating glide line) :

Figure 40a. Generation of the right coset of the subgroup H ( by the element g_v ), demonstrated for a few (areas representing) elements of H .
Element 1 is the identity element, which means the transformation : "do nothing". So if we apply element 1 to the (presupposed) element g_v we just are left with this element g_v . So this element is our first determined element of the right coset of H .
Element a is in fact the element g_h , which means that it is (one time) a horizontal glide reflection along the horizontal dashed line. So if we apply this glide reflection to the presupposed element g_v we get the element b (which is in fact the element g_hg_v ), which is a second element of the right coset of H .

Figure 40b. Generation of the right coset of the subgroup H ( by the element g_v ), demonstrated for yet another (area representing an) element of H .
The element c of H is two times the generating horizontal glide reflection along the dashed line, which is equivalent to a translation along that same line. So if we apply this translation to the presupposed element g_v we get the element d which is a third element of the right coset of H .

The next Figure does the same with all the elements (of H) lying on the horizontal generating glide line.

Figure 41. First phase in the construction of the right coset of the subgroup H ( by the element g_v ).
We successively take an element of the row containing the generating horizontal glide line (and which all are elements of the subgroup H ) and apply it to the element g_v [which is supposed to be already given]. The result is a zig-zag pattern of elements (purple).
[For a good understanding of this we can state (i.e. express) the just mentioned performance to be carried out, in a slightly different but equivalent way : We first take the element g_v (where "take an element" always means that we apply this element to the identity element which leaves it unchanged) and apply to it successively all the elements of the row containing the generating horizontal glide line].
We now have, so to say, handled one (yellow) row of elements of the subgroup H. The next Figures concentrate on the remaining rows.

The next stage of the construction of the right coset of H goes as follows. We take the element g_v and appy to it the transformation (g_v)³ which is an element of H belonging to the row of yellow elements above the row containing the horizontal glide line. The result is one more element indicated by the color green :

Figure 42. Second stage in the construction of the right coset of the subgroup H . One new element (green) is generated.

What we've just done is applying the yellow element of the upper row in the Figure through which (element) the vertical glide line goes (and which [yellow element] is an element of H ), to the (presupposed) element g_v , resulting in the element indicated by the color green.
All the remaining elements of that upper (yellow) row have the form (g_v)³(g_h)^k (where k is a non-zero integer), explained in the next Figure.

Figure 42a. Identification of all the elements of the yellow row above the (yellow) row containing the identity element (1) :
The element (g_v)³ results from three times applying the transformation g_v to the identity element in the upward direction.
All the remaining elements of that (yellow) row have the form (g_v)³(g_h)^k (where k is a non-zero integer), as is shown here for one element, a , which is the element (g_h)³ (so here k = 3 , and if we'd taken the yellow element directly to a's right, then k would have been 4 ). The element a ( = (g_h)³ ) gives, when subjected to the transformation (g_v)³ ( = three times applying the generating vertical glide reflection in the upward direction), the element b ( = (g_v)³(g_h)³ ) , which is indeed an element of the mentioned yellow row.

And this transformation (g_v)³(g_h)^k must be applied to the presupposed element g_v , in order to generate elements of our right coset (of H). So we take the element g_v , apply to it successively (i.e. for all values of k ) a horizontal glide reflection according to the glide line indicated in the Figure followed by three times the vertical glide reflection along the glide line also indicated in the Figure :

Figure 43. Third stage in the construction of the right coset of the subgroup H . One new element (green) is generated. The green arrow indicates one time applying the horizontal generating glide reflection (in the direction to the right) to the presupposed element g_v . The three blue arrows indicate that the result is now subjected to three times the vertical generating glide reflection (in the upward direction).
In fact we have applied the element x (which is g_v³g_h ) of H to the presupposed element g_v , resulting in the element y (green).

In the next Figure we show the generation of one more element of the coset.

Figure 44. Fourth stage in the construction of the right coset of the subgroup H . One new element (green) is generated. The green lines indicate two times (i.e. k = 2) the application of the horizontal generating glide reflection to the presupposed element g_v , while the three blue arrows indicate the application of three times the vertical generating glide reflection to the result.
In fact we have applied the element p (which is g_v³g_h² ) of H to the presupposed element g_v , resulting in the element q (green).

In the same way we can generate further new elements of this coset by applying the remaining elements of this yellow row to the presupposed element g_v , and, finally do the same with respect to all other yellow rows :.

Figure 45. Fifth and final stage in the construction of the right coset of the subgroup H (by the element g_v ). The coset consists of the purple elements.

As one can see, this right coset is different from the corresponding left coset (Figure 40 ), which means that the subgroup H of the parent group P2gg is -- in spite of the fact that this subgroup has the same symmetry as the parent group -- not a normal subgroup.

This concludes our exposition of the Plane Group P2gg with respect to antisymmetry, subpatterns and subgroups.

In the next document we will investigate the plane group Cm with respect to antisymmetry, subpatterns and subgroups.

e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X