
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite one-dimensional periodic patterns, or friezes (sequel)
Reality status of symmetry groups, and the significance of frieze patterns
Before we're going to discuss the friezes in more detail, especially their subgroups, subpatterns, and antisymmetry, we will say something more about the reality status of symmetry groups (i.e. evaluating them ontologically), and about the significance of frieze patterns for the study of natural objects and -- if one wishes to do so -- of objects of ornamental art, which (latter) are very stimulating entities for the development of symmetry theory.
If we speak of the reality status of "symmetry groups", we mean symmetry groups s.l., i.e. including also antisymmetry groups, colored symmetry groups, similarity symmetry groups and conformal symmetry groups.
The very possibility of a group theoretic description (by a group other than C1) of a given intrinsic material structure, i.e. of a self-contained object, points to a definite lawfulness of its actual generation, i.e. a generation of that material object according to a certain law. This law cannot, however, be identified with the group theoretic lawfulness, but is instead a certain dynamical law of the dynamical system that generated that object, and which is a causal physical law.
The law that represents the group (generator set and defining relations) is the ideal (i.e. formal) law expressing part of the metaphysical constitution (in a static after-the-fact sense) of that given object.
The group, (initially just) describing that symmetry, IS that very symmetry of the object. As such it is an ontological cause. This symmetry, taken all by itself, is not a material object but a metaphysical (i.e. ontological) component of the object possessing that symmetry, and as such immaterial, i.e. an objective immaterial 'idea', existing in some immaterial domain, and -- in the present case -- participated by Prime Matter (which is the ultimate substrate of every material thing), in such a way that it becomes an intrinsic property of the given object. It is intrinsic, because it is actually (i.e. inconjunction with concrete matter) generated by a dynamical system whose dynamical law is the essence of that material object. [For the concept of essence, see the Homepage of the website, accessible by
back to homepage ]. So the physical co-generation of a certain symmetry as one of the intrinsic properties of an object is equivalent to the metaphysical co-reception by Prime Matter of that immaterial idea (Form), effecting (part of) the metaphysical constitution of that object. When speaking about "metaphysical (or ontological) components of a thing", recall (from the many discussions about that topic in the First Part of the website, accessible by the just mentioned link) that such 'components' are themselves not things (i.e. not material beings) but preconditions for something to be a thing at all, i.e. they are ontological causes (intrinsic causes) of that thing.
In a long Intermezzo in Part XIII (of the present Series) we have delved a little deeper into the ontological status of symmetry groups and of mathematical structures in general, and found out interesting connections and relationships between symmetry groups and promorphs (stereometric basic forms).
Above we observed that a regular structure (a material object) definitively points to a lawful generation of that structure. The reverse, however, is not in all cases true. Take, for example, Cellular Automata (CA), which are abstract dynamical systems that can generate patterns [For their treatment see the document Cellular Automata in the Non-classical Series of documents in the First Part of the website (See LINK given earlier)].
A finite one-dimensional Cellular Automaton (1-D CA) generates patterned lines (each consisting of a finite number of 'cells' whose state -- f.i. their color -- can change), one after the other, and retaining the earlier generated lines. In this way a sequence of patterned lines is generated together forming a two-dimensional pattern.
Sooner or later, however, it will generate a patterned line that was already generated earlier. From that point onwards the CA will repeat the whole sequence of patterned lines, and will continue to repeat it again and again, resulting in a (periodic) frieze pattern. When it took a long time (i.e. many steps) before a line was finally repeated, the corresponding CA rule (dynamical law) is called 'chaotic', but strictly speaking, it is (still) periodic (Only an infinite CA -- where the lines are infinitely long, i.e. consists of infinitely many cells) could be truly chaotic, never repeating a line that was generated earlier in the sequence). When the period of a 'chaotic' finite CA is indeed very long, we can say that -- staying within the confines of that period -- an irregular structure is generated by a law (the dynamical law of that particular CA) (And indeed, for some infinite CA's this could even be true in the strict sense).
So we can expect irregular patterns in Nature, that are nonetheless generated by a law (and not by perturbations of the system). The (totally) irregular pattern must group theoretically be described as a rosette with symmetry group C1 .
So there are, for example, some Radiolarians (unicellular marine organisms with shells) and other organisms, that are intrinsically asymmetric, and especially so in a more thorough way than is to be found in flatfishes and the like.
But most irregular forms, especially shapes of organisms, are -- as far as the irregularity of their shape is concerned -- the product of more or less random perturbations acting from outside on the growing system which is in itself symmetric, like in many plants. So if we want to consider their intrinsic form, we must subtract those perturbations and (conceptually) let the system grow in a uniform medium. This intrinsic form generally is symmetric according to some symmetry group other than C1 . It is this form we are interested in, and is investigated in Promorphology and Crystallography.
[Promorphology, the study of the ideal stereometric basic form in organisms, is presented on the Second (present) Part of the website at BASIC FORMS : the Series of documents concerning the Promorphological System, accessible by the following LINK : Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology ] [For Crystallography see First Part of website, the documents of the Special Series, accessible by the LINK back to homepage , where one could read the document The Morphology of Crystals, and then (skipping the derivation of Crystal Classes) read the documents about all the Crystal Systems , beginning with The Isometric Crystal System ]
The group in question (describing the intrinsic symmetry of a given object) is then a formal metaphysical (ontological) component of the given object, but causally (in a physical sense) produced by the corresponding dynamical system that generated that object in the first place.
A certain (lower) symmetry can be the effect of symmetry-breaking. There are two kinds of symmetry-breaking.
The first kind is spontaneous symmetry-breaking that happens when the fully symmetrical state of a dynamical system becomes unstable (i.e. that very small disturbances can knock it out of that state into a new state). Because in real situations perturbations are taking place all the time, the system will slide off into a less symmetrical, but stable, state. However, this less symmetrical state is just one of the many possible different less symmetrical states, together embodying the full symmetry that the system originally had. This happens for instance when a falling liquid drop -- which has full rotational symmetry (i.e. involving all angles) with respect to one rotation axis, which is the line down which it falls -- becomes a spiky splash. This spiky splash has limited rotational symmetry (i.e. in order for it to show the same appearance, it can be rotated only through some definite angles, instead of through any angle as is the case in the full rotational symmetry of the falling drop and that of the surface onto which it falls). If we rotate such a resulting splash through an arbitrary angle, then we get an equally possible outcome of the process. So the symmetry is in such a case not actually broken, but shared among the totality of possible outcomes (solutions).
The second kind of symmetry-breaking is induced symmetry-breaking, that happens when a localized force with lower symmetry acts on the given system. Then the full symmetry of the system will be destroyed, resulting in a lower symmetry or no symmetry at all. We could say that this resulting lower symmetry is imposed from the outside. Such an induced symmetry-breaking has important applications, because the behavior (in the broadest sense) of a system that is in some sense 'close' to a perfect symmetric one often retains some traces of that (full) symmetry. Induced symmetry-breaking is a method for handling approximate symmetries, for example those that we encounter in organisms (and which is treated of in the above mentioned Promorphology-section of the Second (present) Part of the website). Indeed, in the promorphology of organisms we speak of the ideal stereometric basic form of them. And even crystals are never perfectly ordered. They show internal dislocations that ruin their intrinsic full symmetry. Of course all other cases of symmetries resulting from spontaneous symmetry-breaking (of higher symmetries) can undergo perturbations, and will do so in reality. We can see this in the symmetry features of splashes, where the resulting crown-shapes (or star-shapes) are seldom absolutely regular.
When we extract the regular symmetry, we have obtained in many cases an intrinsic property of the given object, (a property) as co-product of a certain totality-generating dynamical system on the basis of its inherent dynamical law and given external conditions. [By a totality-generating system we mean a dynamical system that organizes its elements into a single coherent entity, which is an intrinsic totality of features].
Now, as we have seen in the theories of antisymmetry and colored symmetry ( Part II ), we can extend the concept of symmetry considerably. We can describe regular alternations in some object in terms of antisymmetry groups or colored symmetry groups. And also these groups ARE the very symmetries of the given object in which such alternations occur. We can describe the symmetry of such an object as a result of symmetry-breaking, by indicating some higher symmetry group, and then indicating the emerging subgroup (emerging in connection with antisymmetry or colored symmetry, and describing the symmetry of that object), and (also) at the same time describing the symmetry of that object (while not isolating a subgroup from the mentioned higher symmetry group) as a group (derived from that higher symmetry group as generating group) -- antisymmetry group or colored symmetry group -- associated to the mentioned subgroup, a group, that is isomorphic to (but not the same as) the generating group (i.e. the original group from which the antisymmetry or colored symmetry group was derived). So in such a case we have two instances of symmetry-breaking, namely (1) from the original group (generating group) G to a subgroup H (or H1) of it (associated with the corresponding antisymmetry group or colored symmetry group), and (2), from the original group (generating group) G to the antisymmetry group G' or colored symmetry group G*. So the symmetry of that object is then either described by the group H (or H1), or by the antisymmetry group G', or, as the case may be, by the colored symmetry group G*. We will encounter examples in due course.
And apart from this we can describe cases of symmetry-breaking by indicating possible subgroups not associated with antisymmetry or colored symmetry.
In all these cases we have described the symmetry of the given object as the result of symmetry-breaking of a higher symmetry, either resulting in a subgroup associated with antisymmetry or colored symmetry, or resulting in an antisymmetry group or colored symmetry group, or, finally, resulting in a subgroup not associated with antisymmetry or colored symmetry.
But of course, all these symmetries are -- insofar as they are found in the real world -- idealizations, because perturbations will act everywhere in the real world, causing most objects to have no symmetry at all, i.e. causing their symmetry to be isomorphic to the group C1 .
In the previous two documents we have described the symmetry (i.e. ordinary symmetry) of all the seven frieze patterns (line groups). Now we will describe a number of derived symmetries, by noting possible subgroups, antisymmetry groups and one or more examples of colored symmetry groups, derived from those friezes. In an analogous fashion we will later consider also the ornaments G2 , i.e. all the patterns according to the 17 plane groups. As two-dimensional crystals these ornaments will guide us to finally understand three-dimensional crystals and other three-dimensional objects like organisms (In the latter we will also include similarity and conformal symmetries, because many of them allow them to be described by these (non-isometric) symmetries).
But, first of all let us continue with the friezes , which are the most simple periodic patterns, themselves consisting of rosettes G20 in which the invariant subspace is a point, and which are non-periodic structures (i.e. no repetition of a basic unit in such way as to preserve its orientation throughout) described by point groups.
When we call the friezes "one-dimensional periodic patterns" we mean by "one-dimensional" the following : Although the motifs of a frieze are (like those of ornaments, G2) two-dimensional, the only invariant subspaces are lines (which are one-dimensional) (without, however, their points, i.e. the points of those lines, being invariant). This is expressed in the Bohm symbol for friezes : G21 .
The friezes can be encountered in Nature, for example in plant stalks where the leafs all lie in the same plane. And their three-dimensional counterparts can also be found in Nature, for instance in plant stalks where the leafs do not lie in the same plane. These 3-D counterparts are also to be found as atomic rows in real crystals, while the projection of these rows onto a 2-dimensional plane are friezes yet again.
It is interesting to note that friezes appear very early in the history of ornamental art (Paleolithic) (JABLAN, 2002). First as some sort of communication ('messages'), later, when other more sophisticated means of communication were discovered, as purely decorative entities (often inspired by natural objects or phenomena). But, of course, such works of art are not intrinsic (i.e. self-contained) objects like crystals and organisms, which are the main concern of this website.
Antisymmetry in friezes
We will now derive some antisymmetry groups from the friezes, beginning with the frieze p11 :
Figure 1. Pattern according to the line group p11 . The motifs s.l. (oblique strips) are downwards and upwards unbounded. The pattern must be imagined to be extended indefinitely to the right as well as to the left. Group elements are indicated.
One example of an antisymmetry group derived from the above pattern representing the generating group p11 , could be obtained by taking the antiidentity transformation e1 to mean a color exchange bettween the colors red and blue, which means that it changes blue into red, and red into blue. In this example we replace the symmetry generator t (translation) by the antisymmetry generator e1t . This implies the following (where " ==> " means : "will be replaced by" ) :
t ==> e1t .
t2 ==> (e1t)2 = e1te1t = e12t2 = t2 . [Recall that e12 = 1 (meaning no change of color), implying e1 = e1-1, and that e1 commutes with every element of the generating group.].
t3 ==> (e1t)3 = e1t3 .
t-1 ==> (e1t)-1 = t-1e1-1 = t-1e1 = e1t-1 .
t-2 ==> (e1t)-2 = t-2e1-2 = t-2e1-1e1-1 = t-2e12 = t-2 .
The next Figure shows the corresponding color changes and the identities of the group elements of the resulting antisymmetry group.
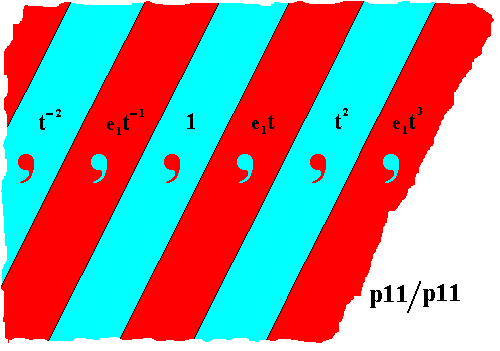
Figure 2. Antisymmetry group, derived from the generating group p11 of Figure 1. The antiidentity transformation e1 changes red into blue, and blue into red.
From Figure 2 we can see that the subgroup, highlighted by the antisymmetry, namely the subgroup { . . . t-2 , 1, t2, . . . }, the blue strips with red commas, has the same structure as the generator group, i.e. it is isomorphic to p11. The antisymmetry group just derived is indicated by the symbol p11 / p11 .
The next Figure shows an example of the group p11 / p11 from ancient ornamental art.
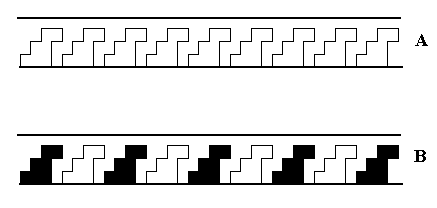
Figure 3.
Bottom image (B) : Antisymmetry frieze p11 / p11 in Neolithic ornamental art. Greece, around 3000 B.C. (After JABLAN, 2002).
Top image (A) : Frieze according to the generating group p11 .
Although we will concentrate on antisymmetry groups (derived from the friezes), it is perhaps instructive to add an example of a colored symmetry group.
These four color permutations together form the cyclic group of order four, C4 . In this group there are no permutations in which one or more colors (letters) stay the same, so we have to do with a regular permutation group.
We now turn to our generating group p11 of Figure 1 and replace the generator t by the colored symmetry transformation ct , where t is a translation (along the frieze axis) and c is the color permutation (ABCD) which is an element of the above mentioned regular color permutation group. If we now generate the color symmetry group by substituting all t's by ct's we'll see the other elements of that permutation group automatically emerge (where ==> means is replaced by) :
t ==> ct
t2 ==> ctct = c2t2 .
t3 ==> ctctct = c3t3 .
t4 ==> ctctctct = c4t4 = t4 (because c4 = 1, the identity permutation).
t5 = t4t ==> t4ct = ct5 .
t6 = t4t2 ==> t4c2t2 = c2t6 .
etc.
t-1 ==> (ct)-1 = t-1c-1 = c-1t-1 = c3t-1 (because c-1 = (DCBA) = (ADCB) = c3 ).
t-2 = t-1t-1 ==> c3t-1c3t-1 = c6t-2 = c4c2t-2 = c2t-2 (because c4 = 1).
etc.
(Where c commutes with every element of the generating group)
We'll start with a version of a p11 pattern, and then carry out the just determined replacements, followed by the corresponding color changes.
Figure 4. A possible realization of the line group p11 . The vertical strips represent motifs s.l. , each containing one motif s.str. (comma). The identities of the group elements are indicated.
We will now execute the replacements as established above, and which are summarized as follows :
t ==> ct
t2 ==> c2t2
t3 ==> c3t3
t4 ==> t4
t5 ==> ct5
t6 ==> c2t6
etc.
t-1 ==> c3t-1
t-2 ==> c2t-2
etc.
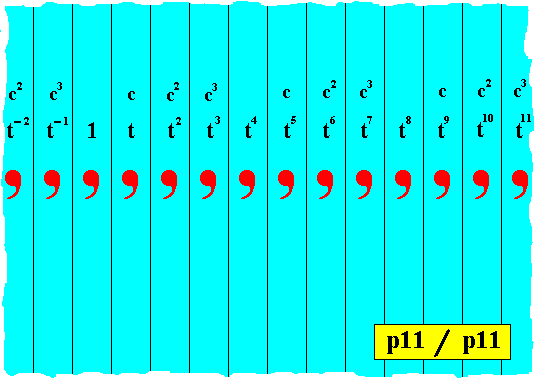
Figure 5. In the p11 pattern of Figure 4 the generator t is replaced by the color-symmetry transformation ct , in order to generate the color symmetry group p11 / p11 for N = 4 (where N is the number of colors used).
The "c-part" and the "t-part" must be read together, for each group element.
In our pattern we used two colors, one for the comma (motif s.str.), red, and one for the background, blue. Let us consider these two colors as initial colors as they are, and remain, present as the colors of the identity element 1. Let us call the red color A, and the blue color B.
c : A ==> B, B ==> C
c2 : A ==> C, B ==> D
c3 : A ==> D, B ==> A
Where
A = red
B = light blue
C = yellow
D = dark blue
So we can now fill in the letters and their corresponding colors in the pattern of the previous Figure.
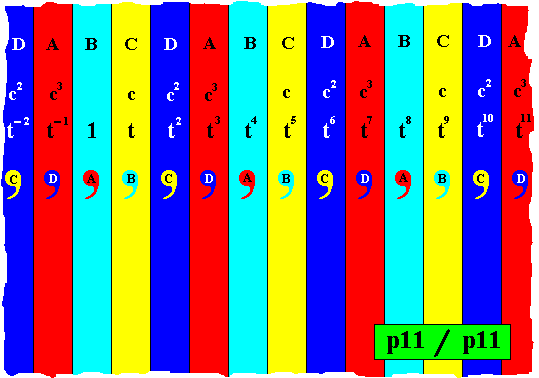
Figure 6. The colored symmetry group p11 / p11 for N = 4 (Color permutation group C4 ), derived from the group p11 as given in Figure 4.
(The colors of the markings are not supposed to play a role as properties of group elements). In reading the group elements the "c-part" should be read together with the "t-part".
In order to let the colors stand out clearly we erase the markings :

Figure 7. The same as previous Figure (group p11 / p11 ), but with the markings erased.
The identity element was set as the light blue element, with red comma, indicated in Figure 6. Any subgroup of our present group (p11 / p11) must contain the identity element. So we can say that the elements represented by the light blue strips form a subgroup of the group p11 / p11 (colored symmetry group for N = 4), and has the same structure as the group p11 which (structure) is Cinfinite .
i(g1g2) = i(g1)i(g2)
which in words is : The image under the function i of the product of any two elements g1 and g2 of the group p11 (generating group) is equal to the product of the images under that same function i . And this means that the two groups p11 and p11 / p11 are isomorphic.
Figure 7 shows that our representation of the colored symmetry group p11 / p11 for N = 4 is a repetition of a sequence of four colors. So it is clear how well colored symmetry groups can describe and analyze structures. Together with ordinary symmetry groups, antisymmetry groups and also (later to be treated) similarity symmetry groups and conformal symmetry groups, we will be able to mathematically elaborate further Haeckel's Tectology (general organic structure theory) and Haeckel's Promorphology (general theory of organic stereometric basic forms), as we have presented them on the present website and which are accessible by Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology.
In all these cases the fundamental structural unit will be some asymmetric structure (that is repeated regularly in some way, a way describable by Group Theory). Such asymmetric unit itself, however, cannot be described by group theory apart from it being just asymmetric and thus as such indicated by the abstract group C1 , that is, the configuration of internal features of such an asymmetric unit cannot be described by group theory. How then should it be described? Well, when such a basic asymmetric structure is an integral part of an intrinsic object, which means that this object is generated by a dynamical system according to a definite dynamical law, then this asymmetric part can, to begin with, be seen as an element of such a dynamical system and organized with other such elements into a larger structure. But in most cases the elements of such a dynamical system are much smaller units, and so we can assume that such asymmetric units (which can themselves be still quite complicated structures) each for themselves have been generated by some subsystem of that dynamical system, and thus generated according to some sub-law (which is part of the overall dynamical law of the whole dynamical system that generated the given object (i.e. the object consisting of regularly arranged asymmetric structural units)). And with this dynamical sub-law we can describe the structure of such an asymmetric unit. So, in the case of an asymmetric structure we cannot give a formal description of it but have to resort to the causal description.
In organisms such an asymmetric unit is very conspicuous, because most organisms have only bilateral symmetry (Described as Eudipleura in our Promorphological System of stereometric basic forms), which means that this asymmetrical unit comprises half of the body. In these cases we also know little about the dynamical law and sub-laws that must have been operated during the formation of such an organism, which means that we -- in order to explain all the many features in a body half -- must resort to an explanation in terms of organic functions, which is akin to the engeneer's approach in explaining structure.
It is instructive to exactly state the difference between, on the one hand, a causally or functionally tracing-back of a given structure (with symmetry as its main aspect) and, on the other hand, a description of this structure in the exact language of mathematics, in our case a description in terms of a symmetry group and its subgroups. This mathematical description is a genuine answer to a WHAT-IS-IT question concerning the given symmetry, while the causally tracing-back (reduction to its physical cause) or the functional explanation (how it works) isn't.
Because a given symmetry can physically equally be generated by one dynamical system or by some other qualitative different but appropriate one (always resulting in it to be an intrinsic property), and, moreover, because it could even have been created in a work of art (always resulting in an extrinsic pattern), a description in these terms (physical cause, work of art), i.e. a description of the symmetry's actual generation, is not a unique answer to the WHAT-IS-IT question. Only a mathematical description (in terms of group theory) provides such an answer.
The generation of the symmetry group (which is isomorphic to some abstract group) is the formal 'generation' of that particular symmetry. The symmetry group is f o r m, received by a material substrate, and is an integral part of the ontological constitution of the object possessing that particular symmetry. Also symmetry-breaking is a formal aspect of some physical process. And because the WHAT-IS-IT of something is at the same time its ontological cause, the symmetry group is the ontological cause of that given symmetry, its legitimation, so to say, to exist. And as received onto a material substrate the symmetry group is one of the ontological causes of the given object.
We will now continue our study of antisymmetry groups derived from the friezes.
This line group can be represented by the following frieze pattern :
Figure 8. Frieze pattern according to the line group p12 . Here the colors red and blue do not represent symmetry features, but only serve to highlight the group elements as represented by areas. The one-dimensional point lattice is indicated by yellow dots and connection lines.
In order to derive an antisymmetry group from the symmetry group p12 we replace the generator t (translation) by the antisymmetry transformation e1t , where e1 is the antiidentity transformation, which can stand for a color change between two colors, here taken to be red and blue, and which commutes with every element of the generating group. The other generator, namely h (half-turn about a certain point) will not be replaced. The mentioned rotation point of the half-turn in the above Figure and in the next Figure is implied to be coincident with the lattice point associated with the identity element.
t ==> e1t .
t2 ==> (e1t)2 = e1te1t = e12 t2 = t2 .
t3 ==> (e1t)3 = e13 t3 = e12e1t3 = e1t3 .
t4 ==> (e1t)4 = e12e12 t4 = t4 .
t5 ==> (e1t)5 = e1t5 .
etc.
t-1 ==> (e1t)-1 = t-1e1-1 = t-1e1 [ because e1e1 = 1, and e1e1-1 = 1,
therefore e1 = e1-1 ] = e1t-1 .
t-2 ==> (e1t)-2 = t-2e1-2 = t-2e1-1e1-1 = t-2e1e1 = t-2 .
etc.
The next Figure shows the result, and as such represents the antisymmetry group p12 / p12 derived from the (generating) group p12 .
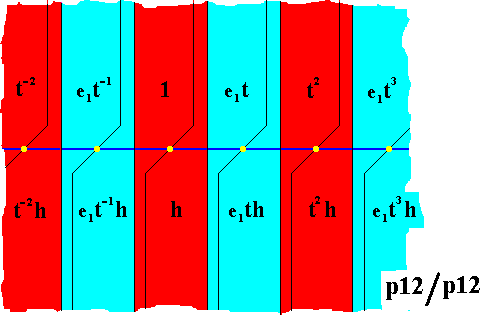
Figure 9. Antisymmetry group p12 / p12 derived from the symmetry group p12 (Figure 8). The antisymmetry is expressed by the alternation of blue and red. The one-dimensional point lattice is indicated by yellow dots and connection lines.
As can be seen from the above Figure, the set of red elements contains the identity element and is a subgroup of the antisymmetry group. This subgroup is -- as can also be seen from the Figure -- isomorphic to the group p12 .
The next Figure gives an example of the antisymmetry group p12 / p12 from ancient ornamental art.
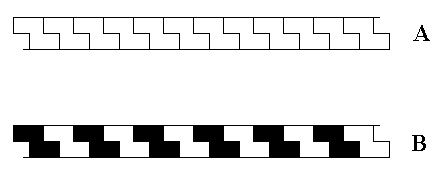
Figure 10.
Top image (A) : Generating frieze p12 .
Bottom image (B) : Antisymmetry frieze p12 / p12 in Neolithic ornamental art, Greece. (After JABLAN, 2000)
This pattern can mathematically be derived as an antisymmetry group from A.
In the pattern representing the symmetry group p12 , as given in Figure 8, we can also recognize a subgroup not associated with antisymmetry or colored symmetry, namely the subgroup {1, h}, which is the group C2 (cyclic group of order 2). See next Figure.
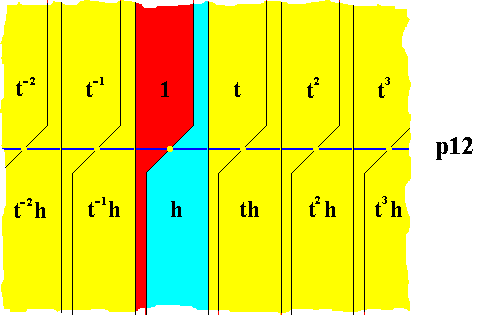
Figure 10a. Subgroup of the group p12 consisting of the elements 1 (identity element) and h (half-turn about the lattice point between these two elements). The colors red and blue do not represent symmetry features, but serve to highlight the two elements of the subgroup.
Such a subgroup can be interpreted as the result of symmetry-breaking (desymmetrization) of the group p12 .
A second antisymmetry group can be derived from the group p12 when the generator h (half-turn about a fixed point) is replaced by the antisymmetry transformation e1h , while the generator t is not being replaced. Doing so we get the following :
h ==> e1h .
1 = hh ==> e1he1h = e12h2 = h2 = 1 .
The result is shown in the next Figure.
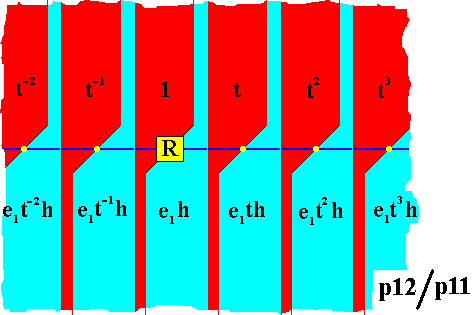
Figure 11. Pattern representing the antisymmetry group p12 / p11 derived from the pattern of Figure 8 representing the group p12 . The element e1h is a half-turn about the point R followed by a color change between the colors red and blue.
The set of red elements in the above Figure contains the identity element and is a subgroup of the antisymmetry group. As can be seen from the Figure this subgroup is isomorphic to the group p11 (It consists just of the translation of an asymmetric figure (motif)). On the basis of this the antisymmetry group is denoted by the symbol p12 / p11 .
The next Figure gives an example of the antisymmetry group p12 / p11 from ancient ornamental art.
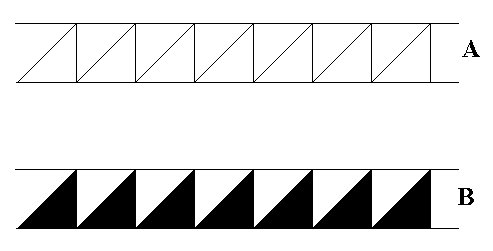
Figure 12.
Top image (A) : Pattern representing the generating symmetry group p12 .
Bottom image (B) : Antisymmetry frieze p12 / p11 in Neolithic ornamental art, Near East, around 5000 B.C. (After JABLAN, 2002). This pattern can be derived as antisymmetry group from A.
The next group from which we will derive antisymmetry groups is the frieze p1m . For a pattern representing this generating group, see next Figure.
Figure 13. Frieze pattern representing the line group p1m . The colors red and blue do not signify symmetry features, but only serve to indicate group elements. Lattice nodes of the one-dimensional point lattice are indicated by yellow dots. The elements t (translation) and m (reflection in the mirror line m ) have been taken as generators.
The first antisymmetry group will be derived by replacing the generator t (translation) by the antisymmetry transformation e1t , while the other generator (m) is not replaced. The antiidentity transformation e1 will stand for a color change between red and blue. The replacements will be the same as was the case with the antisymmetry group p12 / p12 :
t ==> e1t .
t2 ==> (e1t)2 = e1te1t = e12 t2 = t2 .
t3 ==> (e1t)3 = e13 t3 = e12e1t3 = e1t3 .
t4 ==> (e1t)4 = e12e12 t4 = t4 .
t5 ==> (e1t)5 = e1t5 .
etc.
t-1 ==> (e1t)-1 = t-1e1-1 = t-1e1 [ because e1e1 = 1, and e1e1-1 = 1,
therefore e1 = e1-1 ] = e1t-1 .
t-2 ==> (e1t)-2 = t-2e1-2 = t-2e1-1e1-1 = t-2e1e1 = t-2 .
etc.
The resulting antisymmetry group p1m / p1m is shown in the next Figure.
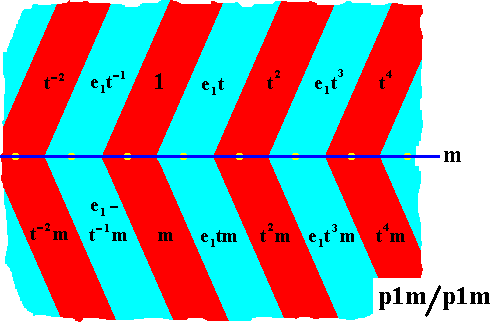
Figure 14. Antisymmetry frieze p1m / p1m derived from the group p1m (previous Figure).
The set of red elements (containing the identity element) is a subgroup of this antisymmetry group and is -- as can be seen in the Figure -- isomorphic to the group p1m , and because of this the symbol for the antisymmetry group is p1m / p1m .
The next Figure gives an example of the antisymmetry group p1m / p1m in ancient ornamental art.
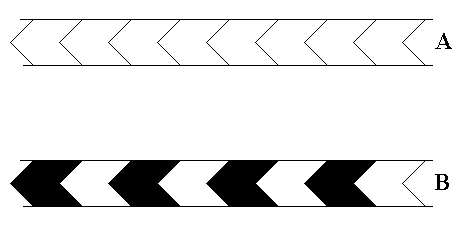
Figure 15.
Top image (A) : Frieze pattern according to the generating group p1m .
Bottom image (B) : Antisymmetry frieze p1m / p1m in Neolithic ornamental art, Near East, around 5000 B.C. (After JABLAN, 2002).
This frieze can mathematically be derived as antisymmetry group from A.
A second antisymmetry group can be derived from the group p1m , namely the antisymmetry group p1m / p11 . In order to do so we replace the generator m (reflection in the frieze axis) by the antisymmetry transformation e1m , where e1 is again the antiidentity transformation, that effects a color change between two colors.
m ==> e1m .
The next Figure gives the result of the replacements, namely the antisymmetry group p1m / p11 .
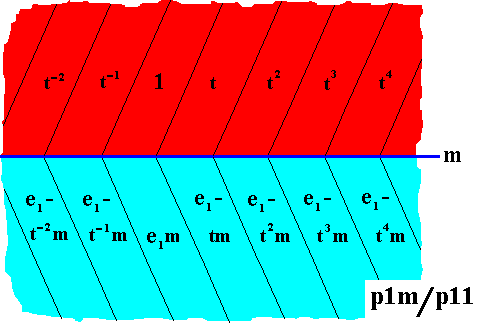
Figure 16. Pattern according to the antisymmetry group p1m / p11 derived from the symmetry group p1m as realized by the pattern of Figure 13. The antiidentity transformation e1 effects a color change between the two colors red and blue.
The "e1-part" and the "tm-part" (or "m-part") should be read together.
The set of red elements in the above Figure, containing the identity element, is a subgroup of the antisymmetry group p1m / p11 and -- as can be seen in the Figure -- is isomorphic to the line group p11 . Therefore the symbol for this antisymmetry group is p1m / p11 .
The next Figure gives an example of the antisymmetry group p1m / p11 in ancient ornamental art.
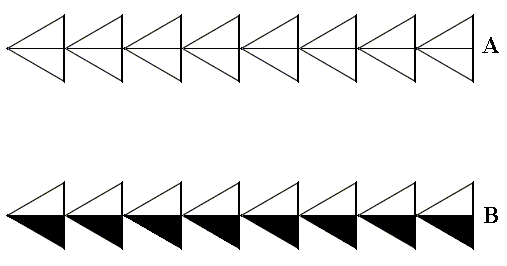
Figure 17.
Top image (A) : Pattern representing the generating group p1m .
Bottom image (B) : Antisymmetry frieze p1m / p11 in Neolithic ornamental art, Near East. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
The next antisymmetry group that can be derived from the symmetry group p1m is the group p1m / p1g . We can do so by replacing the generator t by the antisymmetry transformation e1t and the generator m by the antisymmetry transformation e1m . Where e1 is the antiidentity transformation effecting a color change between two colors, where further e12 = 1 (no color change), and where e1-1 = e1 . When we do this we get the following :
t ==> e1t .
t2 ==> (e1t)2 = e1te1t = e12 t2 = t2 .
t3 ==> (e1t)3 = e13 t3 = e12e1t3 = e1t3 .
t4 ==> (e1t)4 = e12e12 t4 = t4 .
t5 ==> (e1t)5 = e1t5 .
etc.
t-1 ==> (e1t)-1 = t-1e1-1 = t-1e1 [ because e1e1 = 1, and e1e1-1 = 1,
therefore e1 = e1-1 ] = e1t-1 .
t-2 ==> (e1t)-2 = t-2e1-2 = t-2e1-1e1-1 = t-2e1e1 = t-2 .
etc.
m ==> e1m .
tm ==> e1te1m = e12tm = tm .
t2m ==> e1te1te1m = e1t2m .
t3m = tt2m ==> e1te1t2m = t3m .
etc.
t-1m ==> (e1t)-1e1m = t-1e1-1e1m = t-1e1e1m = t-1m .
t-2m = t-1t-1m ==> e1t-1e1t-1e1m = e1t-2m .
etc.
The resulting antisymmetry group p1m / p1g is shown in the next Figure.
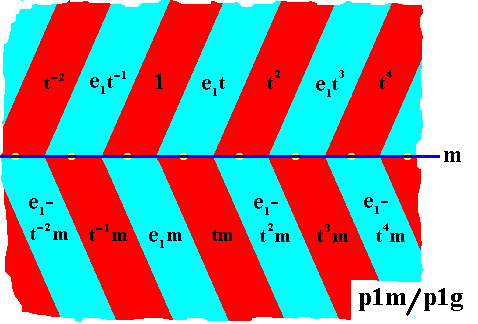
Figure 18. Antisymmetry group p1m / p1g , derived from the generating group p1m as represented in Figure 13. The antiidentity transformation e1 effects a color change between the colors red and blue.
In the above Figure we can see that the red elements (among which is the identity element) form a subgroup that is isomorphic to the group p1g , which is the reason why the symbol of the antisymmetry group is p1m / p1g .
The next Figure gives an example of the antisymmetry group p1m / p1g in ancient ornamental art.
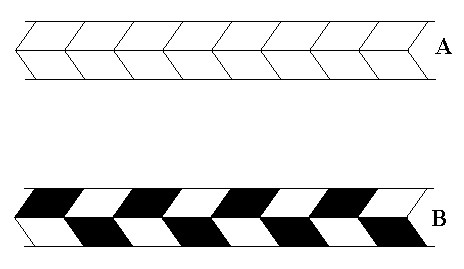
Figure 19.
Top image (A) : Pattern representing generating symmetry group p1m .
Bottom image (B) : Antisymmetry frieze p1m / p1g in Neolithic ornamental art, Anadolia, around 5000 B.C. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
In the pattern representing the group p1m , as in Figure 13, we can recognize a subgroup not connected with antisymmetry or colored symmetry, namely the subgroup {1, m}, which is the group D1 , which is isomorphic to C2 .
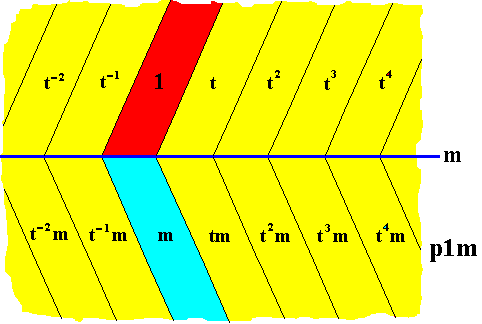
Figure 20. Subgroup {1, m} of the group p1m . The colors red and blue do not signify symmetry features, but only serve to indicate the two group elements of the subgroup.
The next line group from which we will derive antisymmetry groups is the group pm1 .
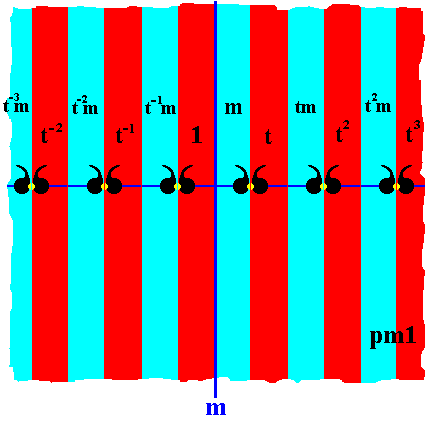
Figure 21. Frieze pattern according to the line group pm1 .
The colors red and blue do not signify symmetry features, but only serve to indicate group elements. Lattice points of the one-dimensional point lattice are indicated by yellow dots related to each other by lattice connection lines. The generators used are t (translation) and m (reflection in the line m . The pattern must be imagined to be extended indefinitely to the right as well as to the left.
The next Figure is the same as Figure 21, but now having the areas representing group elements all with the same color (In the subsequent antisymmetry frieze this color red will be changed to blue when the antiidentity transformation e1 is part of the transformation representing the group element).
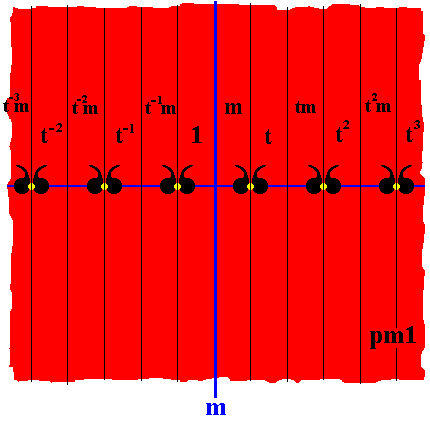
Figure 21a. The generating group pm1 . Group elements indicated by vertical boundary lines and the elements' identities.
We will now derive the antisymmetry group pm1 / pm1 from the group pm1 by replacing the generator t by the antisymmetry transformation e1t , resulting in an alternation of the two colors (we take : red and blue), as we saw in previous examples.
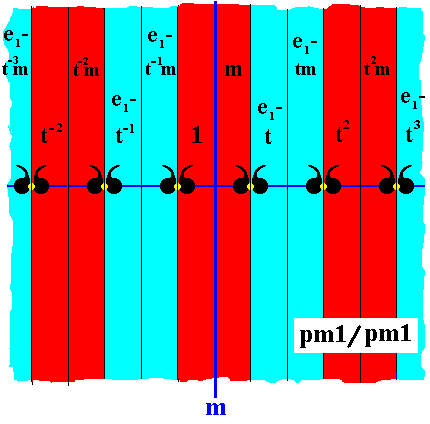
Figure 22. Pattern representing antisymmetry group pm1 / pm1 derived from the group pm1 as given in the previous Figure. The "e1-part" and the "tm-part" (or the "t-part") must be read together.
From the above Figure we can see that the red elements (with among them the identity element) form a subgroup which is isomorphic to the group pm1 , so the symbol for the corresponding antisymmetry group is pm1 /pm1 .
The next Figure gives another example of this antisymmetry group.
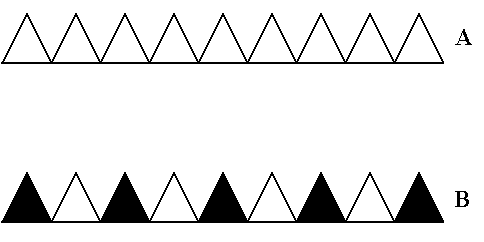
Figure 23.
Top image (A) : Frieze pattern according to the generating symmetry group pm1 .
Bottom image (B) : Antisymmetry frieze pm1 / pm1 , derived from A.
The second antisymmetry group that can be derived from the line group pm1 is the group pm1 / p11 .
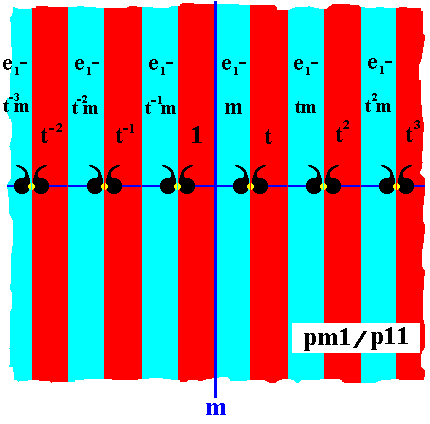
Figure 24. Pattern according to the antisymmetry group pm1 / p11 derived from the symmetry group pm1 . The antiidentity transformation e1 effects a color change from red to blue.
The "e1-part" must be read together with the "tm-part" or "m-part".
In the above Figure we see that the red elements (which have among them the identity element) form the subgroup {. . . t-2, t-1, 1, t, t2, t3, . . . } of the antisymmetry group. This subgroup is evidently isomorphic to the line group p11 , therefore the symbol for the antisymmetry group is pm1 / p11 .
In our pattern, as depicted above, we have (drawn) units (black commas) of the motifs s.str. . They just serve to express the asymmetric quality of the fundamental region and its copies. But if we would like to involve them in the color swap in virtue of the antiidentity transformation e1 , then their initial color must be blue (which is then transformed into red where appropriate). The next Figure illustrates this.
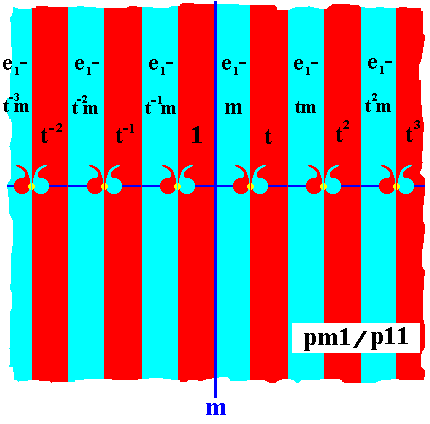
Figure 24a. Antisymmetry group pm1 / p11 .
The commas are now involved in the color permutation ( Red Blue ) according to the antiidentity transformation e1 .
The next Figure gives an example of the antisymmetry group pm1 / p11 in ancient ornamental art.
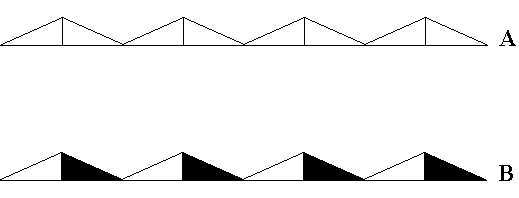
Figure 25.
Top image (A) : Pattern according to generating group pm1 .
Bottom image (B) : Antisymmetry frieze in Neolithic ornamental art, Near East. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry group from A.
The next line group from which we will derive antisymmetry groups is the group pmg . The next Figure depicts a possible realization of this group.
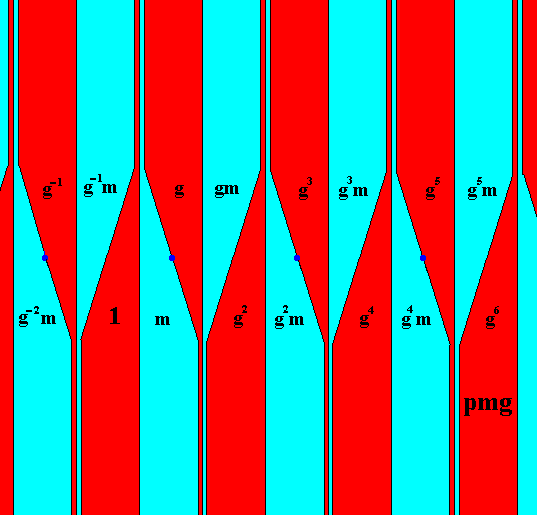
Figure 26. Identification of the group elements in a pattern according to the line group pmg . Each element is represented by a fundamental area or one of its copies (red, blue). The colors red and blue of the areas do not signify symmetry features of the pmg pattern, only the geometry does so.
The next Figure gives this same generating group pmg but now letting all the areas representing group elements have the same color. When we derive an antisymmetry group we will set the color red as the initial color (The color of the identity element) and change it into blue according to the color permutation e1 .
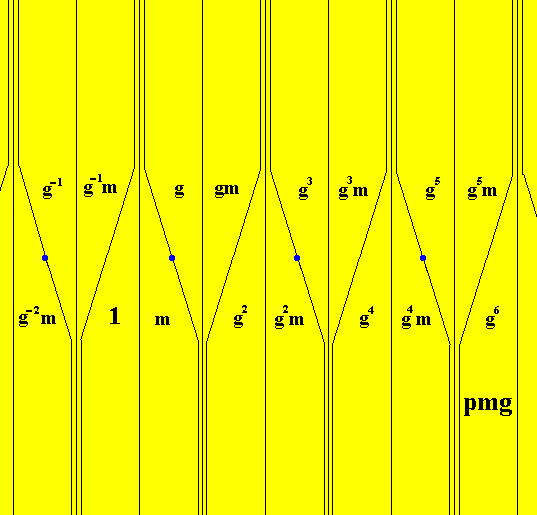
Figure 27. The generating symmetry group pmg with the areas representing group elements having the same color. The shape of these areas completely expresses the asymmetry of the basic unit of the pattern. In deriving antisymmetry groups we will set the initial color as the color red.
First we will derive the antisymmetry group pmg / pm1 , by replacing the generator g by the antisymmetry transformation e1g , where the antiidentity transformation effects a color change from the initial color red to the color blue. So we have :
g ==> e1g .
g2 ==> (e1g)2 = e1ge1g = e12g2 = g2 .
g3 = gg2 ==> e1gg2 = e1g3 .
etc.
g-1 ==> (e1g)-1 = g-1e1-1 = g-1e1 = e1g-1 .
g-2 = g-1g-1 ==> e1g-1e1g-1 = e12g-2 = g-2 .
etc.
The result of these replacements is given in the next Figure.
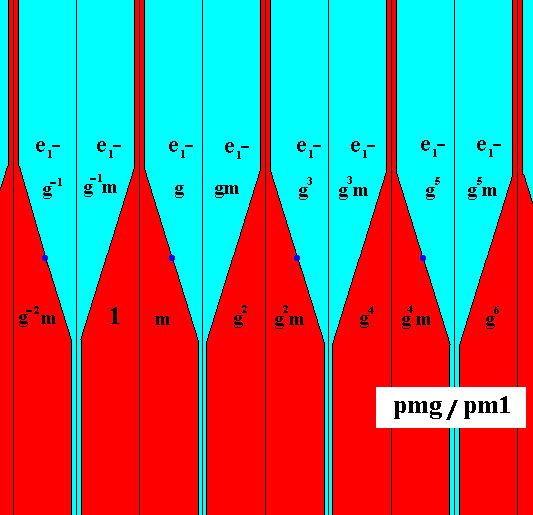
Figure 28. Pattern according to the antisymmetry group pmg / pm1 derived from the generating symmetry group pmg as given in the previous Figure.
The antiidentity transformation e1 effects a color change from red to blue.
The "e1-part" must be read together with the "gm-part" or the "g-part".
In the above Figure we see that the set of red elements (with among them the identity element) forms a subgroup of the antisymmetry group, and is isomorphic to the line group pm1 , so the symbol for this antisymmetry group is pmg / pm1 .
The next Figure gives an example of the antisymmetry group pmg / pm1 in ancient ornamental art.
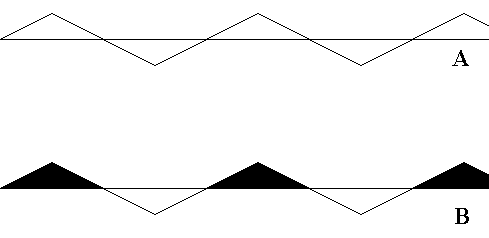
Figure 29.
Top image (A) : Pattern according to the generating symmetry group pmg .
Bottom image (B) : Antisymmetry frieze in Neolithic ornamental art, Greece. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry pattern from A.
We can yet derive another antisymmetry group, but isomorphic to pmg / pm1 , from the group pmg , by replacing the group element g2 -- which is a translation -- by the antisymmetry element e1g2 , which is an antisymmetry transformation amounting to two times applying the glide reflection g followed by a color change. We then get the following :
g ==> g ( g is not a translation ).
g2 ==> e1g2 . This is a translation, let us call it t . In fact we will change color from red to blue or blue to red after every such translation, according to the color permutation (Red Blue) (cycle notation). So when we have two such translations, the original color is restored.
g3 ==> g3 ( g3 is not a translation ).
g4 = g2g2 ==> e1g2e1g2 = e12g4 = g4 ( g4 = t2 ).
g5 ==> g5 ( g5 is not a translation ).
g6 = g2g2g2 ==> e1g2e1g2e1g2 = e1g6 . ( g6 = t3 ).
g7 ==> g7 ( g7 is not a translation ).
g8 = (g2)4 ( = t4 ) ==> e1g2e1g2e1g2e1g2 = e12e12(g2)4 = g8 .
g9 ==> g9 ( g9 is not a translation ).
g10 = g2g8 ==> e1g2g8 = e1g10 .
g11 ==> g11 ( g11 is not a translation ).
g12 = g2g10 ==> e1g2e1g10 = e12g12 = g12 .
g13 ==> g13 ( g13 is not a translation ).
g14 = g2g12 ==> e1g2g12 = e1g14 .
g15 ==> g15 ( g15 is not a translation ).
etc.
g-1 ==> g-1 ( g-1 is not a translation ).
g-2 = (g2)-1 ==> (e1g2)-1 = g-2e1-1 = g-2e1 = e1g-2 . ( g-2 is a translation, namely t-1 ).
g-3 ==> g-3 ( g-3 is not a translation ).
g-4 (which is t-2 ) = g-2g-2 ==> e1g-2e1g-2 = e12g-4 = g-4 .
g-5 ==> g-5 ( g-5 is not a translation ).
g-6 = g-2g-2g-2 ==> e1g-2e1g-2e1g-2 = e12e1g-6 = e1g-6 .
g-7 ==> g-7 ( g-7 is not a translation ).
g-8 = g-2g-6 ==> e1g-2e1g-6 = e12g-8 = g-8 .
g-9 ==> g-9 ( g-9 is not a translation ).
g-10 = g-2g-8 ==> e1g-2g-8 = e1g-10 .
g-11 ==> g-11 ( g-11 is not a translation ).
g-12 = g-2g-10 ==> e1g-2e1g-10 = e12g-12 = g-12 .
g-13 ==> g-13 ( g-13 is not a translation ).
g-14 = g-2g-12 ==> e1g-2g-12 = e1g-14 .
g-15 ==> g-15 ( g-15 is not a translation ).
etc.
Further we know that the identity element 1 can be expressed as mm and this remains unaffected by the replacement of g2 by e1g2 , so
1 ==> 1 , and of course
m ==> m .
And of course in all elements containing in their symbol, in addition to a gn , an m , like for instance g3m , we can ignore the m when determining the new element and its corresponding color. Thus, because g3 ==> g3, g3m ==> g3m . And because g2 ==> e1g2, g2m ==> e1g2m .
We set the initial color as the color red, that is, the identity element is set as red. And as soon as there is one e1 present in the symbol of the new group element, the color red will be changed into blue.
In the next table we summarize the above determined replacements and indicate the resulting color for each case :
| 1 ==> 1 | m ==> m | ||
| g ==> g | g-1 ==> g-1 | ||
| g2 ==> e1g2 | g-2 ==> e1g-2 | ||
| g3 ==> g3 | g-3 ==> g-3 | ||
| g4 ==> g4 | g-4 ==> g-4 | ||
| g5 ==> g5 | g-5 ==> g-5 | ||
| g6 ==> e1g6 | g-6 ==> e1g-6 | ||
| g7 ==> g7 | g-7 ==> g-7 | ||
| g8 ==> g8 | g-8 ==> g-8 | ||
| g9 ==> g9 | g-9 ==> g-9 | ||
| g10 ==> e1g10 | g-10 ==> e1g-10 | ||
| g11 ==> g11 | g-11 ==> g-11 | ||
| g12 ==> g12 | g-12 ==> g-12 | ||
| g13 ==> g13 | g-13 ==> g-13 | ||
| g14 ==> e1g14 | g-14 ==> e1g-14 | ||
| g15 ==> g15 | g-15 ==> g-15 |
The next Figure shows the result of these replacements, and thus gives the antisymmetry group pmg / pm1 .
Figure 30. Pattern according to the (second example of the) antisymmetry group pmg / pm1 derived from the generator symmetry group pmg by replacing the element g2 (which is a translation) by the antisymmetry element e1g2 (which is a translation followed by a color change from red to blue). The "e1-part" must be read together with the "gm-part" or the "g-part".
It is perhaps instructive to depict a pattern according to the just determined second example of an antisymmetry group pmg / pm1 derived from the symmetry group pmg , where more repetitions are visible. (As in all cases the patterns must be imagined to be extended indefinitely to the right as well as to the left.) :
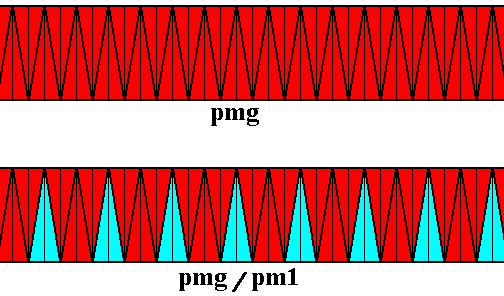
Figure 31.
Top image : Pattern representing the generating symmetry group pmg . Every asymmetric triangular area represents a group element.
Bottom image : Derived (from top image) pattern representing the antisymmetry group pmg / pm1 .
Compare with Figure 30.
Let us elaborate a little on the above Figure in order to explain that the generating pattern depicted in the top image of Figure 31 is indeed according to the line group pmg . See next Figures.
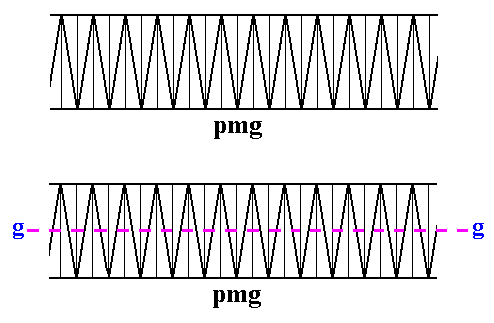
Figure 32. Pattern according to the line group pmg (top image), and, the same pattern with the glide line g (being the symmetry element of the glide reflection g ) indicated (dashed purple line). Every asymmetric area represents a group element.
The next Figure shows the workings of repeated application of the glide reflection along the frieze axis.
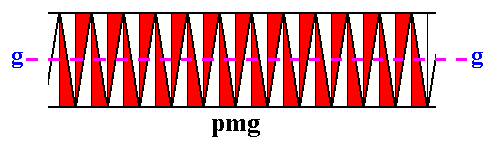
Figure 33. Action of the repeated glide reflection, applied to a group element of the pattern of Figure 32.
This glide reflection at the same time relates larger units :
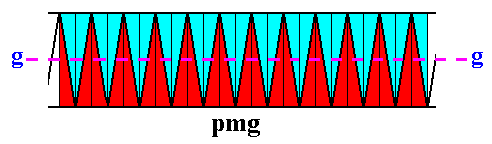
Figure 34. Action of the repeated glide relection on a larger unit of the pmg pattern of the previous Figures.
Because of the presence of the glide line and of reflection perpendicular to the frieze axis we know that we indeed have to do with the line group pmg .
The next Figure gives an example of this second antisymmetry group pmg / pm1 from ancient ornamental art.
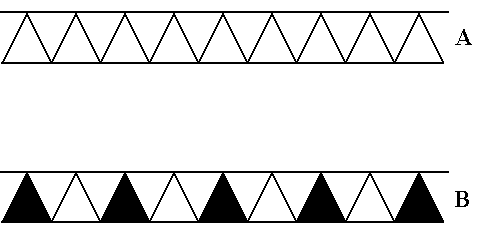
Figure 35.
Top image (A) : Pattern according to the generating symmetry group pmg .
Bottom image (B) : Antisymmetry frieze in Neolithic ornamental art, Near East. (After JABLAN, 2002).
This pattern can mathematically be derived as antisymmetry pattern from A.
In the next document we will continue to derive antisymmetry groups from the line group pmg and from the remaining line groups.
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II
Back to subpatterns and subgroups Part III
Back to subpatterns and subgroups Part IV