
e-mail :

Sequel to Group Theory
We'll start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.
Infinite one-dimensional periodic patterns, or friezes
The seven symmetry groups of Friezes G21
A Frieze is a periodic pattern of two-dimensional motifs repeating in one direction (and of course also in the opposite direction) only. It is based on a one-dimensional point lattice, i.e. an infinite sequence of equidistant points arranged in a linear series. The motifs of a frieze are two-dimensional. As motifs s.str. (motifs in the narrow sense) they are certain definite two-dimensional more or less isolated figures, linearly arranged along an infinite line. As motifs s.l. (motifs in the broadest sense) they also include the background, and this means that such a motif (s.l.) extends along the translation line till half-way to the next motif, and that it extends indefinitely in the directions perpendicular to the translation axis. That's why we can say that the frieze is 'carried' by the two-dimensional plane (and is a subgroup of this plane, when the latter is seen as an infinite and continuous group of symmetries) [ NOTE 1 ]. And this plane stays where it is when the symmetries of the frieze are applied, so this plane is invariant with respect to the symmetry groups of friezes, but not its points. But because this plane is just the carrier (or substrate) of the frieze pattern it is not accounted for as invariant space in the symbol for the category of friezes, but accounted for as representing the dimensionality of the motifs of the frieze, which is the meaning of the subscript 2 in the Bohm symbol G21 denoting the group category. But although the points of the plane (carrying a frieze) are not invariant with respect to the group, some lines are (but not their points : to be sure, there are invariant points, but they are only invariant with respect to a certain symmetry transformation -- a certain group element -- not with respect to all transformations of the given group). These invariant lines are parallel to, and/or incident with, the translation axis, and are, as the dimensionality of invariant subspaces, denoted by the subscript 1 in the Bohm symbol G21 denoting the group category of friezes. The presence of these invariant lines distinguishes the friezes from ornaments (described by the 17 Plane Groups), because in ornaments no lines are invariant, as well as no points (with respect to the group). On the other hand the motifs of ornaments are also two-dimensional, so their Bohm symbol is accordingly G2 , the symmetry groups of ornaments.
There are in total seven different symmetry groups of (discrete) friezes (where some of them are isomorphic to each other). In two of them we can detect infinitely many lines, all parallel to the translation axis, that are invariant under all symmetry transformations of such a frieze. In the remaining friezes only the translation axis itself is invariant. Because of these invariant lines we call such groups (i.e. all frieze groups) line groups.
The next Figure gives a realization of the seven symmetry groups of friezes.
Figure 1. The seven Friezes (strip patterns) G21 .
The patterns must be imagined to extend indefinitely to the right as well as to the left.
We will now elaborate on these friezes, discussing motif s.str., motif s.l., fundamental region, group elements, symmetry elements and subgroups (Of the latter we will give one example, and elaborate on them further down [from Part V onwards]).
First we show the point lattice on which all frieze patterns are based. It consists of linearly arranged equidistant points (lattice points).

Figure 2. The translational point lattice describing the arrangements of motifs (motifs s.l ) in the seven symmetry types (symmetry groups) of frieze patterns. The lattice points emerge in virtue of a multiplication accomplished by a translation t of an initial lattice point.
We will characterize every group underlying a frieze pattern by its presentation and structure :
Presentation and structure :
p11
{t}
Structure Cinfinite
Where t is a translation parallel to the frieze axis.
We can now associate with each lattice point (Figure 2) a motif s.str. (i.e. a motif in the narrow sense). When such a motif s.str. is a comma, or some other asymmetric figure, we get the frieze p11 , which is an infinite group consisting only of translations . . . t-2, t-1, t, t2, t3, . . . and the identity element.

Figure 3. The frieze pattern p11 with lattice points (red) and auxiliary connection lines indicated. The commas are the motifs s.str.
The pattern must be imagined to extend indefinitely to the right as well as to the left.
The next Figure indicates these same motifs s.str. (commas) as well as the motifs s.l (red and blue areas). The motifs s.l. extend indefinitely upwards as well as downwards, and of course the frieze extends indefinitely to the left as well as to the right. The different colors red and blue do not signify an asymmetry, but only serve to show the motifs s.l.. By definition the motifs s.l. are equivalent areas of the pattern, which means that each lattice node (lattice point) is in the same way associated with a motif s.l. (which includes the motif s.str.), which in turn means that the lattice describes the way of repetition of the motifs s.l.
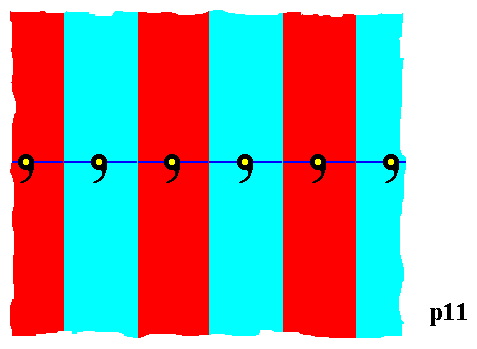
Figure 4. Indication of the motifs s.l. (red and blue areas) of the p11 pattern of Figure 1. The lattice points (nodes) are indicated by yellow dots. The commas are the motifs s.str.
The motifs s.l. extend indefinitely upwards and downwards (each such motif s.l. extending beyond the lattice connection line), while the frieze extends indefinitly to the left and to the right. The whole pattern is carried by the plane E2.
The ordering and repetition of the motifs s.l. is according to the geometry of the point lattice.
In this case, namely the group p11 , the motif s.l. coincides with the fundamental region or any copy of it, which means that the motif s.l. can represent a group element.
For an analogous treatment of, and introduction to, the concepts and geometric representations of : motif s.l., motif s.str., representation and generation of group elements, in ornaments (that represent the 17 plane groups), see the Third Part of Website -- accessible by Third Part of Website , and there the Series Crystals and the Implicate Order, Part I -- XIX, where one can, to begin with, look up the treatment of the group P4, and then, if necessary, of the other plane groups considered in the remaining Parts of that Series.
The next Figure again shows the motifs s.l. in the p11 pattern, which as such can represent group elements. Two such group elements are indicated, namely the initial element (identity element) 1 and the generator element t , which is a translation.
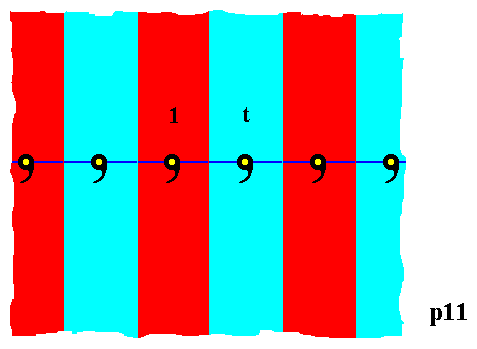
Figure 5. Two group elements of the p11 pattern are indicated (their geometric representations and those of all other group elements -- red and blue areas -- extend beyond the lattice connection line, implying that in the present case (p11) each group element is represented by a vertical band, extending indefinitely upwards as well as downwards). The two group elements indicated are the initial element 1 (i.e. the element to begin with, when the group is generated, and which is at the same time the identity element of the group), and the generator element t , which generates the group when it is repeatedly applied to the initial element.
The next Figure shows the (representation of the) group elements . . . t-2, t-1, 1, t, t2, t3, . . . of the group p11 , or, equivalently, its generation.
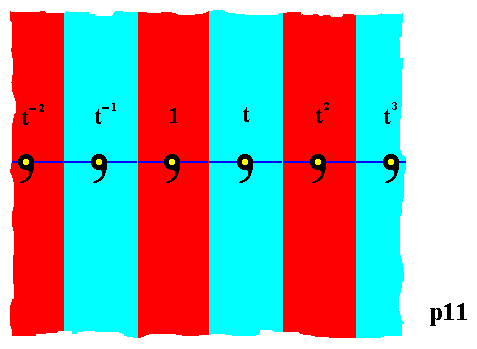
Figure 6. Generation of the group elements (represented by red or blue vertical bands) by the translation t (and its inverse t-1 ) of the group p11.
In fact, in the present case, we can use areas lacking (as just areas) reflectional symmetry, as it is indeed absent in the motif s.str. (comma), in virtue of the form and orientation of these areas, representing group elements, as the next Figure shows :
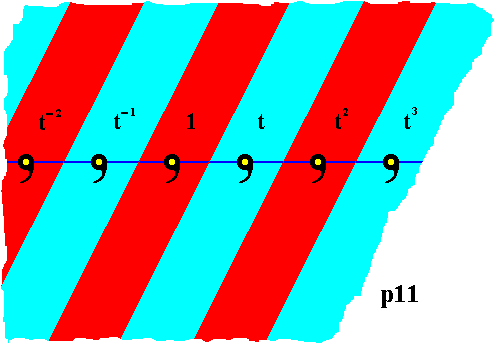
Figure 6a. Maximal areas representing group elements of the group p11 . The shape and orientation of the areas, with respect to the one-dimensional lattice underlying the pattern, express the absence of mirror symmetry of the motifs s.str.
As we can see in the above Figure, the areas do not lack all symmetry, as is the case for the motifs s.str. They still possess a two-fold rotation axis. So in the present case (p11) we cannot represent the motifs s.str. fully by the shape and orientation of areas representing group elements.
All subgroups of the frieze p11 are, like p11 itself, infinite, and are themselves also p11 patterns. The group as well as each of its subgroups have a countable infinite number of elements, so the elements of the group can be set in a one-to-one correspondence with those of any of its subgroups, while it is at the same time obvious that products are preserved. So the group and any of its subgroups are isomorphic to each other. Such a subgroup can be formed by the generator t n , where n is a whole number, except 1 and zero. The next Figure illustrates this for n = 2, which means that we have the generator t2 and its inverse t-2 .

Figure 7. Subgroup of the group p11 , generated by the element t2
and its inverse t-2 .
Top image : The group p11 , represented by a pattern of equidistant commas.
Center image : The subgroup p11 of the group p11 .
Bottom image : The group p11 with (one of) its (possible) subgroup(s) (red) indicated.
Later we will extensively consider subgroups of the seven frieze symmetry types.
Presentation and structure :
p1g
{g}
Structure Cinfinite
Where g is a glide reflection parallel to the frieze axis.
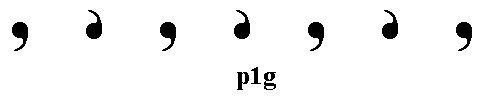
Figure 8. A frieze pattern according to the group p1g .
The pattern must be imagined to extend indefinitely to the right as well as to the left.
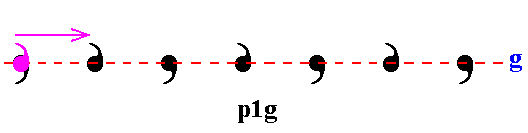
Figure 9. Expounding the glide reflection g , being the generator of the group p1g , along the glide reflection line g . The glide reflection is a commutative combination of a reflection (purple) in the glide reflection line and a translation (arrow) parallel to that line.
The next Figure shows the one-dimensional point lattice that indicates the repetition of a unit (which is, ultimately, the motif s.l.), resulting in the p1g pattern. The lattice points indicate equivalent areas of the pattern.
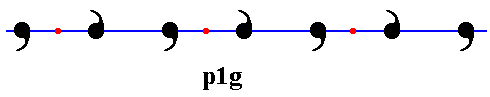
Figure 10. Indication of the lattice points (red) underlying the p1g frieze pattern. With each lattice point there are associated two motif units (commas) of the motif s.str. , which is itself consisting of two such units.
On the basis of the above Figure we can determine the motifs s.l. of our p1g pattern :
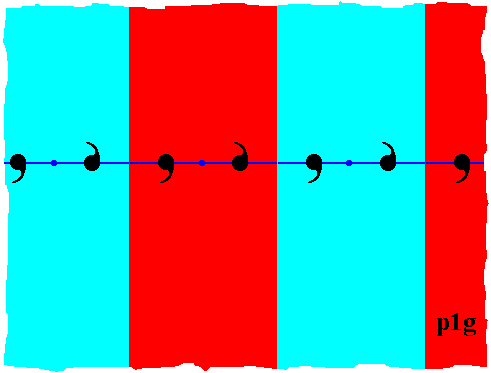
Figure 11. Indication of the motifs s.l. (red and blue areas). The red and blue colors do not signify an asymmetry, they only serve to highlight the motifs s.l.
Each motif s.l. is associated with a lattice point, and consists of two units (commas) of the motif s.str. PLUS corresponding background (extending above and below the lattice node connection line). So the motifs s.l. are vertical stripes unbounded downwards as well as upwards.
We're now going to determine the maximal areas representing group elements, i.e. the fundamental region (and its copies) of our p1g pattern. In the present case this means that the motifs s.l. must each be split up. See next Figures.
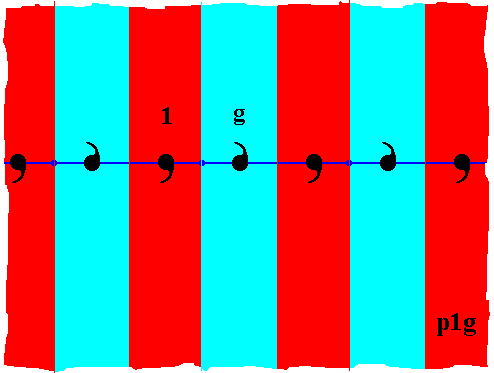
Figure 12. Partitioning of the motifs s.l. , such that the resulting areas (red, blue) represent group elements. Two such elements are named, the identity element 1 and the generator g , which is a glide reflection along the axis of the frieze. So the group elements of the p1g pattern are represented by vertical stripes.
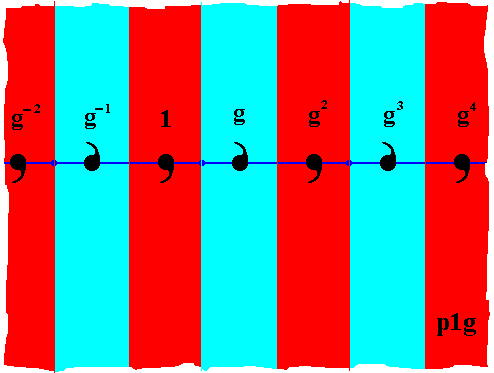
Figure 13. Naming of the other group elements (of the p1g pattern) generated by the generator element g (This generation goes, of course, on indefinitely, letting expand the pattern to the right as well as to the left).
Presentation and structure :
pm1
{t, m} m2 = (mt)2 = 1, or
{m1, m2} m12 = m22 = 1. (m2 = m1t)
Structure Dinfinite .
Where m , m1 and m2 are reflections perpendicular to the frieze axis, and t a translation parallel to the frieze axis.

Figure 14. A realization of the group pm1 .
The pattern must be imagined to extend indefinitely to the right as well as to the left.
The next Figure indicates the lattice nodes. Each node is associated with a motif s.str. consisting of two motif units (commas). As such the nodes are associated with equivalent areas of the pattern. They describe the repetition of equal units.

Figure 15. Situation of the nodes (red dots) of the one-dimensional point lattice describing the repetition of units, resulting in a pm1 pattern. Each node (lattice point) is associated with a motif s.str. , which consists of two symmetrically placed motif units (commas). As such each lattice node is associated with a motif s.l.
On the basis of the above Figure we can determine the motifs s.l. of our pm1 pattern :
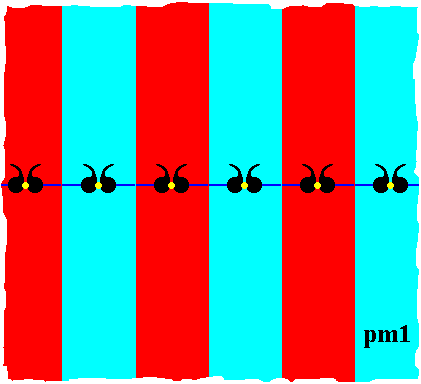
Figure 16. Indication of the motifs s.l. (red and blue) of the pm1 pattern. Each motif s.l. is a vertical strip (extending below and above the lattice connection line) consisting of a motif s.str. (itself consisting of two motif units (commas)) PLUS corresponding background. In the upward and downward direction these motifs s.l. are unbounded. The motifs s.l. are arranged according to the one-dimensional lattice (lattice points indicated by yellow dots). The colors red and blue do not signify any asymmetry, but serve to highlight the motifs s.l.
In order to determine the maximal areas representing group elements, we must partition each motif s.l. in two parts. See next Figure.
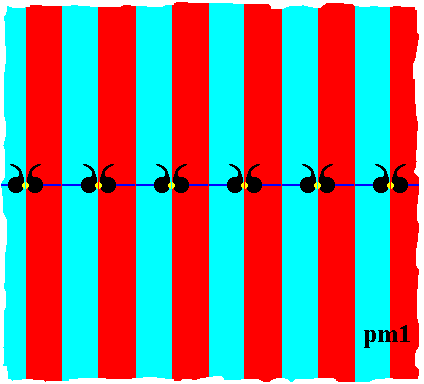
Figure 17. Partition of the motifs s.l. such that the resulting regions (red, blue) are maximal areas representing group elements. So each group element is represented by a vertical strip (upwards and downwards unbounded) containing one unit (comma) of the motif s.str. The red and blue colors do not signify any asymmetry, but serve to highlight the (representation of) group elements.
The next Figure indicates a chosen area to represent the identity element (initial element), and the areas representing a possible set of generators { t, m }.
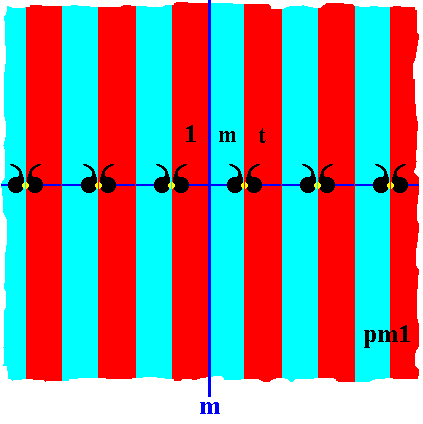
Figure 18. Areas, representing group elements. Three of those areas are chosen to represent the identity element and two generators t (translation) and m (reflection in the mirror line perpendicular to the frieze axis).
The generation of the group pm1 can now be expressed by marking the remaining areas with the proper symbols of group elements :
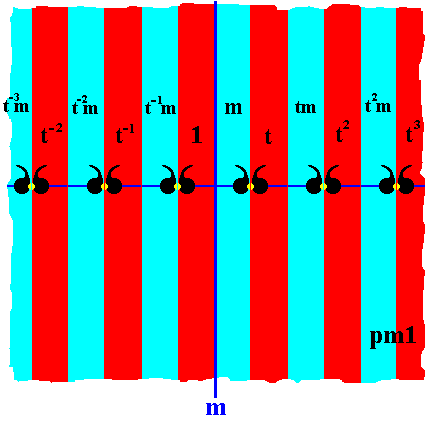
Figure 19. Marking the areas representing group elements in terms of the generators t and m .
Presentation and structure :
p12
{t, h} h2 = (ht)2 = 1, or
{h, h1} h2 = h12 = 1 (h1 = ht)
Structure Dinfinite .
Where t is a translation, h and h1 half-turns.
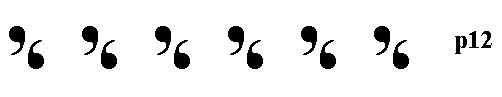
Figure 20. Frieze pattern according to the group p12 .
The pattern must be imagined to extend indefinitely to the right and to the left.
The next Figure indicates the lattice nodes of the p12 pattern.

Figure 21. Situation of the nodes (red dots) of the one-dimensional point lattice describing the repetition of units, resulting in a p12 pattern. Each node (lattice point) is associated with a motif s.str. , which consists of two motif units (commas) related to each other by a half-turn. As such each lattice node is associated with a motif s.l.
The next Figure indicates the motifs s.l. of our p12 pattern.
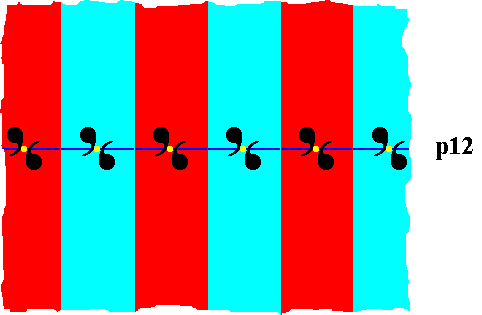
Figure 22. Motifs s.l. (blue, red) of the p12 pattern. Each such motif s.l. is associated with a lattice node, extends indefinitely upwards as well as downwards -- and is thus represented by a vertical stripe -- and contains one motif s.str. consisting of two motif units (commas) related to each other by a half-turn. The colors red and blue do not signify any asymmetry but only serve to highlight the motifs s.l . The lattice nodes are represented by yellow dots.
We're now going to partition these motifs s.l. in such a way that we obtain maximal areas that represent group elements. See next Figure.
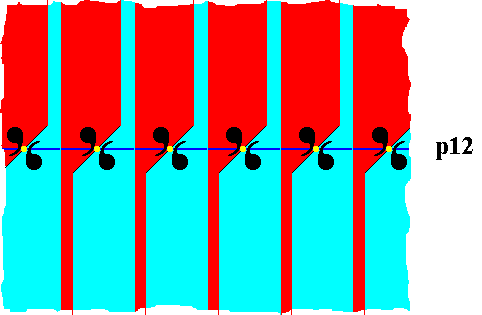
Figure 23. Partition of the motifs s.l. of the p12 pattern, resulting in maximal areas (red, blue) representing (also by their shape) group elements. Each such area contains one unit (comma) of the motif s.str. and extends indefinitely upwards and downwards. The colors red and blue do not signify any asymmetry but only serve to highlight the areas representing group elements. These areas represent a fundamental region and its copies.
As the above Figure shows, this is the first frieze where the shape and orientation of the areas representing group elements can express fully the asymmetry of the units of the motif s.str. .
The next Figure shows this same pattern (p12), where one area is chosen to represent the identity element (initial element) 1 , and two others to represent the generators t (translation) and h (half-turn about the point R ).
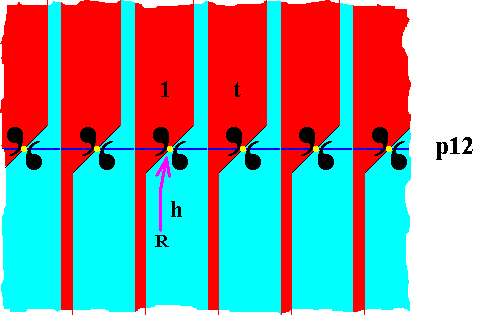
Figure 24. The p12 pattern as in the previous Figure. Three areas are marked to represent the identity element and two generators, a horizontal translation and a half-turn about the point R .
We can now generate the remaining group elements of the displayed part of the pattern, i.e. we can mark the remaining areas representing group elements :
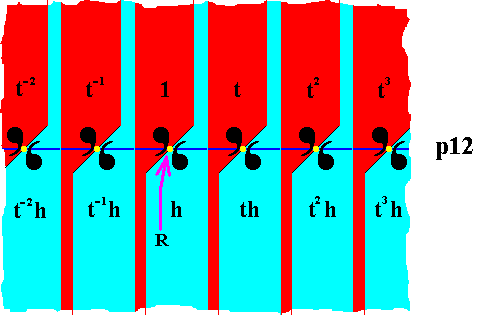
Figure 25. Filling in of the areas of the p12 pattern, representing group elements, by their proper identities.
Because in this case the asymmetry of the motif units (commas) of the motif s.str. can be fully expressed by the shape and orientation of the areas representing group elements, we can dispose of those commas in expressing the p12 pattern. See next Figure.
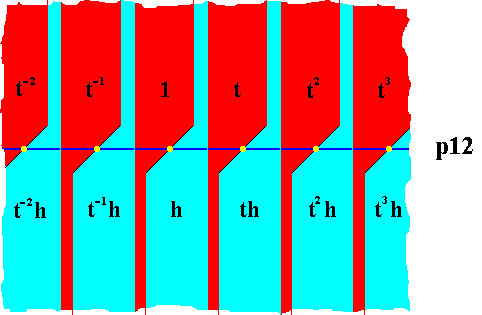
Figure 26. The same as previous Figure, but now with the commas removed. The resulting pattern fully represents the group p12 . The colors red and blue do not represent asymmetries, but only serve to indicate the areas representing group elements.
In the next document we will continue the investigation of friezes (line groups), starting with the next frieze pattern according to the group pmg .
e-mail : 
To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology)
Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology
Back to subpatterns and subgroups (introduction)
Back to subpatterns and subgroups Part II