2-D patterns XXIII

The Symmetry of Two-dimensional Patterns

As prelude to the symmetry of three-dimensional crystals and organisms

Subpatterns and Subgroups Part XXIII (Subgroups and Antisymmetry in Ornaments)

e-mail :

Sequel to Group Theory

As always, we start with reminding the reader about the "Important Remark" near the end of Part III of Group Theory (To see it, click HERE and then go to (end of) Part III ), a Remark concerning the direction of reading products of group elements, like, say, apq. We read such products (from that Remark onwards) from back to front. Thus (with respect to apq) first q, then p, and then a.

Infinite two-dimensional periodic patterns, or Ornaments (sequel)

In the previous two documents we have investigated antisymmetry patterns, and subpatterns representing-, and subpatterns-not-representing subgroups, all derivable from Cm patterns. Further we have analyzed an ornament from Neolithic art allegedly derived as antisymmetry pattern from a Cm pattern.
In the present document we will investigate the Plane Group C2mm as to its possible antisymmetries, subpatterns and subgroups.

The Plane Group C2mm

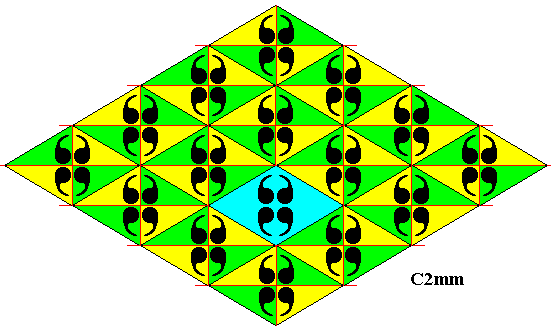
In Figure 1 we show a periodic two-dimensional pattern representing the plane group C2mm. It can be based on a rhombic lattice, as is done here (It can also be based on a centered rectangular lattice).

Figure 1. Pattern representing plane group C2mm . The motifs s.str. are (chosen to be) a set of four commas, and as such placed inside the (rhombic) lattice meshes. The commas in a mesh are related to each other by horizontal and vertical reflection lines. A quarter of a rhombic lattice mesh can represent a fundamental region (yellow or green), containing an asymmetric unit (comma) of the motif s.str. , and as such it represents a group element. A lattice mesh is indicated (blue). The pattern must be imagined to extend indefinitely over the plane.

In deriving antisymmetry patterns from the above C2mm pattern, we set the background color to be blue. As such it is the generating symmetry pattern with respect to the antisymmetry patterns to be derived from it.
The next Figure shows the point lattice of this generating C2mm pattern.

Figure 2. Rhombic point lattice (indicated by connection lines) of the generating C2mm pattern.

Figure 3. Generators of the above C2mm pattern :
Reflection m_h in the horizontal line m_h .
Reflection m_v in the vertical line m_v .
Translation t_ne in the NE (north-east) direction (red arrow).
Translation t_se in the SE (south-east) direction (red arrow).
In order to generate the C2mm pattern we start with the (area representing the) identity element (green), and apply to it the two reflections. The result is a pattern with D₂ symmetry. In the next Figure we subject this D₂ pattern to the generating translation t_se .

Figure 4. Application of the generating translation t_se to the above generated D₂ motif. If we now subject the result to the generating translation t_ne we get the whole C2mm pattern.

In deriving antisymmetry patterns from our C2mm pattern we interpret the antiidentity transformation e₁ as being the color permutation (Blue Red) (cycle notation, which here -- as also in all previous cases -- means : Blue ==> Red, Red ==> Blue), with respect to the background color. The initial background color will be set as blue. Antisymmetry patterns (representing antisymmetry groups) will emerge when we replace one or more generators of our starting pattern by their corresponding antisymmetry transformations. Our pattern of departure (generating C2mm symmetry pattern) will then be as follows :

Figure 5. Starting pattern representing the plane group C2mm . Its identity element (1) and its generators (m_h , m_v , t_ne and t_se ) are indicated.

The first antisymmetry pattern to be derived from the generating C2mm pattern of Figure 5 can be obtained by replacing the generating horizontal reflection m_h by its corresponding antisymmetry transformation e₁m_h .
In the Figures below, we indicate the generators of the initial C2mm pattern. But of course, the generating horizontal reflection, indicated by m_h , has now become the corresponding antisymmetry reflection e₁m_h .
We will derive the antisymmetry pattern in several steps.

Figure 6. If we subject the identity element (1) to the antisymmetry transformation e₁m_h the result must have its background color changed from blue to red (Here, for the time being, indicated by the transition from green to purple. These colors will later be restored to blue and red.)

Figure 7. When we subject the identity element and the newly generated element of the previous Figure to the reflection m_v (which is not an antisymmetry transformation), their background colors will not be changed.

Figure 8. Repeated application of the generating translations t_ne and t_se to the result of the previous Figure does not bring about color changes, because (here) these translations are not antisymmetry transformations.

If we now restore the colors (green ==> blue, purple ==> red) we get the following antisymmetry pattern :

Figure 9. Antisymmetry pattern (representing the antisymmetry group C2mm / Cm) derived from the generating C2mm pattern of Figure 5, by replacing the generating reflection m_h by the antisymmetry transformation e₁m_h .

When we isolate the blue elements of the just derived antisymmetry pattern we get the following subpattern :

Figure 10. Isolated subpattern consisting of the blue elements of the just derived antisymmetry pattern. It contains the identity element of the antisymmetry patttern.

The isolated subpattern can be generated by subjecting the identity element by the vertical reflection m_v . We have now two elements. When we repreatedly subject both elements to the translations t_ne and t_se , we get the whole subpattern. And because the identity element of the subpattern is also the identity element of the generating C2mm pattern as well as of the derived antisymmetry pattern, and because its generator elements (m_v , t_ne and t_se ) are also elements of the generating C2mm pattern and of the derived antisymmetry pattern (and, consequently, this also holds for all elements obtained by all combinations of the mentioned generators), our subpattern is a subgroup of the generating as well as of the antisymmetry pattern, and its symmetry is that of the plane group Cm. Therefore the symbol for the antisymmetry group represented by the just derived antisymmetry pattern must read C2mm / Cm .

The point lattice of the above derived subpattern can either be given as a rhombic lattice or as a centered rectangular lattice :

Figure 11. Rhombic point lattice (indicated by strong dark blue connection lines) of the isolated subpattern consisting of the blue elements of the just derived antisymmetry pattern.

Figure 12. Centered rectangular point lattice (indicated by strong dark blue connection lines) of the isolated subpattern consisting of the blue elements of the just derived antisymmetry pattern.

Figure 13. Centered rectangular point lattice (indicated by strong dark blue connection lines and red dots) of the isolated subpattern consisting of the blue elements of the just derived antisymmetry pattern. The lattice points are indicated by red dots.

Figure 14. Rhombic point lattice (indicated by strong dark blue connection lines) of the above derived antisymmetry pattern (Figure 9 ). Compare with the point lattice of the generating C2mm symmetry pattern of Figure 2 .

The next antisymmetry pattern to be derived from the generating C2mm pattern of Figure 5 can be obtained by replacing the generating NE translation t_ne by the antisymmetry transformation e₁t_ne , where the antiidentity transformation e₁ is again interpreted as the color permutation (Blue Red) (cycle notation) with respect to the background color, which initially is set to be blue.
In the Figures below, we indicate the generators of the initial C2mm pattern. But of course, the generating NE translation t_ne has now become the corresponding antisymmetry translation e₁t_ne .
We will derive the antisymmetry pattern in several steps.

Figure 15. First step in the derivation of the above defined antisymmetry pattern from the generating C2mm pattern. From the identity element we generate three more elements by the horizontal and vertical reflections. Because these reflections are not antisymmetry transformations they do not involve color change. So the initial color of the identity element is also the color of the three new elements ( This color is, for the time being, indicated by green, which will later be restored to blue).

Figure 16. Second step in the derivation of the above defined antisymmetry pattern from the generating C2mm pattern. If the elements already present (1, m_h , m_vm_h and m_v ) are subjected to the antisymmetry translation t_ne , we get an alternation of colors, because e₁t_nee₁t_ne = t_ne² , and e₁t_nee₁t_nee₁t_nee₁t_ne = (e₁t_ne)⁴ = t_ne⁴ , etc.
The colors green and purple will latter be restored to blue and red.

Figure 17. Third step in the derivation of the above defined antisymmetry pattern from the generating C2mm pattern. If the elements already present are subjected to the generating SE translation t_se no color change will occur, because this translation is not an antisymmetry transformation. The next Figure restores the colors.

Figure 18. Final step in the derivation of the above defined antisymmetry pattern from the generating C2mm pattern. The colors green and purple are restored to blue and red.
This antisymmetry pattern was thus derived from the generating C2mm pattern by replacing the NE translation by its corresponding antisymmetry translation.

The point lattice of the above antisymmetry pattern is indicated in the next two Figures.

Figure 19. Point lattice (indicated by strong dark blue connection lines) of the just derived antisymmetry pattern. It is an oblique lattice. Compare with the point lattice of the generating C2mm symmetry pattern (Figure 2 )

Figure 20. Point lattice (indicated by strong dark blue connection lines) of the just derived antisymmetry pattern. A unit mesh is indicated by yellow outline and alternative colors.

In order to correctly identify the just derived antisymmetry group, let's isolate the subpattern of blue elements from the pattern of the above Figure. First, however, we give the just derived antisymmetry pattern without indication of symmetry elements (mirror lines).

Figure 21. Antisymmetry pattern as derived above (Figure 18) without indication of symmetry elements (mirror lines).

Figure 22. The subpattern consisting of the blue elements of the just derived antisymmetry pattern isolated.

Figure 23. Same as previous Figure. Some superfluous lines erased.

The next Figure indicates the point lattice of the isolated subpattern of blue elements.

Figure 24. Point lattice (indicated by strong red connection lines) of the s u b p a t t e r n (blue elements) of the above derived antisymmetry pattern (Figure 18 ) (derived by replacing the generating NE translation by its corresponding antisymmetry translation). It is an oblique lattice. The o r i g i n a l (area representing the) identity element -- i.e. that of the generating C2mm symmetry pattern as well as that of the antisymmetry pattern derived from it -- is indicated (yellow).

In the above Figure it is clear that the subpattern of blue elements consists of an asymmetric motif that is repeated by two independent translations. So it represents a group, and its symmetry is according to the plane group P1 . Although the motifs s.str. (each consisting of four commas) are mirror symmetric in two lines, these symmetries are not at the same time symmetries of the whole pattern. Therefore the motifs must be assessed as being asymmetric. Starting from one part of such a motif, we cannot generate the other parts by symmetry transformations that are symmetry transformations of the whole subpattern.
But this means that the identity element (and any other group element) of this subpattern must be represented by four commas, because this represents the asymmetric motif that is being repeated by the only symmetry transformations the pattern possesses (See next Figure) : The NE and SE generating translations. We may note that the NE generating (meaning that it can be a generator) translation of our subpattern is twice as long as the generating NE translation of the generating (i.e. generating the antisymmetry pattern) C2mm symmetry pattern (Figure 5 ).
All this implies that our P1 subpattern is not a s u b g r o u p of the group representing the generating C2mm symmetry pattern, nor of the group representing the antisymmetry pattern that was derived from it. Therefore the symbol of the antisymmetry group derived above should -- according to conventions established earlier -- read C2mm / *P1 .

Figure 25. Subpattern (of blue elements, and its underlying lattice) of the above derived antisymmetry pattern (Figure 18 ). Superfluous lines removed. The symmetry of this subpattern is that of P1 . The content of a lattice mesh coincides with a group element. A chosen location of the identity element ( 1 ) of this P1 group, and thus the area representing it, is indicated by yellow coloring. It is different from the area representing the identity element of the generating C2mm symmetry pattern (Figure 5 , where the triangular area, including one comma, represents the identity element), or of the antisymmetry pattern (Figure 18 , where the triangular area, including one comma, represents the identity element). Therefore the subpattern, although having the structure of a group, is not a subgroup the latter patterns.

In the next document we will continue our investigation concerning antisymmetry, subpatterns and subgroups of patterns representing the plane group C2mm.

e-mail :

To continue click HERE for further group theoretic preparation to the study of the structure of three-dimensional crystals (crystallography) and the basic symmetry of organisms (promorphology).

back to homepage

Back to 3-dimensional crystals (conclusion), Organic Tectology and Promorphology

Back to subpatterns and subgroups (introduction)

Back to subpatterns and subgroups Part II

Back to subpatterns and subgroups Part III

Back to subpatterns and subgroups Part IV

Back to subpatterns and subgroups Part V

Back to subpatterns and subgroups Part VI

Back to subpatterns and subgroups Part VII

Back to subpatterns and subgroups Part VIII

Back to subpatterns and subgroups Part IX

Back to subpatterns and subgroups Part X