Symmetries, Transformations, and Groups

Every object can be characterized by its  s y m m e t r y.  It contains at least one, but often several symmetries. But what then is a symmetry?
A symmetry is a certain operation, namely a rigid transformation, that can be applied to that object such, that the result is that same object occupying exactly the same space as it occupied before the transformation took place. The object has covered itself exactly, or, in other words, it is mapped onto itself. The transformation is rigid, which means that all internal distances and angles are preserved. But, except for the so-called identical transformation, most points have swapped their positions.
A good example are the symmetries of the Equilateral Triangle.

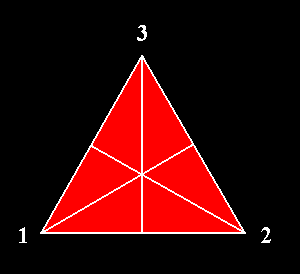
Figure 1.  An equilateral triangle. The three points associated with its three angle are numbered.

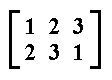
If, on the other hand, we rotate the triangle 240⁰ it will also cover the original. It again occupies the same space as before. The permutation involved is the following :

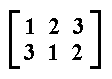
If we, finally rotate it 360⁰ we have executed an operation which is in fact equivalent to not having it rotated at all. The permutation involved is the following :

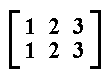
This permutation represents the identical transformation.
So to begin with the equilateral triangle has three symmetries :   three rotational symmetries, one of which -- rotation of 0 or 360 degrees -- is the identical transformation, in which no points are swapped.
But the equilateral triangle has still more symmetries.
We can detect three mirror lines (reflection lines), each one going from a tip to the center of the opposite side (Figure 1). When we reflect the triangle with respect to one such reflection line we swap the two halves of the triangle divided by that line. Also these three reflections can be expressed by permutations of the three numbered points of the triangle (Figure 1) :   When we reflect the triangle with respect to the vertical mirror line, 2 will be replaced by 1, and 1 will be replaced by 2, while 3 will be 'replaced' by itself. So we have the following permutation :

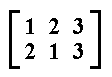
The permutations representing the other two reflections are then as follows :

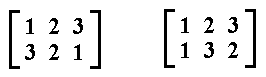
So we have six permutations with respect to the Equilateral Triangle, i.e. the equilateral triangle has six symmetries, which are rigid transformations such that the original is exactly covered by the image produced by that transformation :  three rotational symmetries (one of which is the identical transformation) and three reflectional symmetries.
In the following we list all these six permutations and identify each one of them with a letter for easy reference.

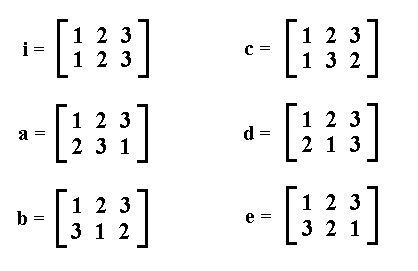
Now this set of transformations -- the permutations i, a, b, c, d, and e -- i.e. the set of symmetries possessed by the Equilateral Triangle, is not just a set, it is not just a bunch of symmetries that happen to be present at the triangle. The set has a  s t r u c t u r e,  causing it to be an intrinsic unity. Let me explain this structure.
The permutations associated with the Equilateral Triangle are related to each other in a special way :   They can be seen as elements of an  o p e r a t i o n,  in our case a binary operation, which means that the two members of each pair of permutations from our set can in some way be combined. And the result of this combination -- the product of the operation -- turns out to be identical with some one permutation already present in our set. And this combination -- this operation -- with respect to (any) two permutations of our set consists in the  s u c c e s s i v e   e x e c u t i o n  of two permutations (one after the other). The result of such an operation on any two permutations of our set turns out to be always itself a permutation already present in our set. Of course this was to be expected, because the permutations are in our case transformations of an equilateral triangle, such that the image (the product) of this transformation exactly covers the original triangle. So performing two cover transformations, one after the other, results again in a covering of the image triangle onto the original. We can say that our set of permutations is closed under the operation mentioned (which is the successive application of two permutations of the set). We can denote this operation by the letter O.
Let us subject the permutations  a and  c (in this order) to the operation O, i.e. let us successively apply the permutations  a and  c :

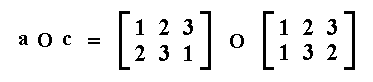
The result of the application of permutation  a  on the initial numbers  1  2  3  is :   2  3  1.  To this result we will apply permutation  c :

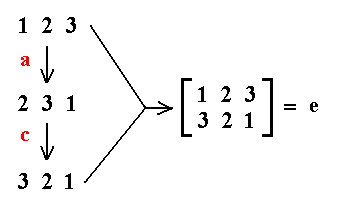
We can easily verify that the result is identical to permutation e, which already belongs to our set of permutations, so we can state :

In this way we can determine all the possible combinations of two permutations of our set. The results can conveniently be summarized in the following table :

This table reads as follows :  If we want to know the outcome of  d  O  e  we look up  d  in the column of entries to the left (i.e. left of the line), and we look up  e  in the row of entries above (i.e. above the line), and determine what is found at the intersection of the horizontal line, starting from  d,  and the vertical line, starting from  e.  We find  a.
The contents of the table immediately shows that the set is closed under the operation. But, in addition to the fact that our set of permutations is closed under the operation O, there is more to the structure of this set :

The operation O is associative, which means that to any three elements x, y and z of our set of permutations the following applies :

That our operation complies with associativity is intuitively clear : Our operation consists in the successive execution of two transformations : The end result (and that is all what matters here) is the same when we (1) shave and wash, and then, after a pauze, dress, or when we (2) shave, and, after a pauze wash and dress.

And further :  every equation

and every equation

possesses one, and not more than one solution.

We can check this for every two elements of our set by consulting the table given above.

These properties (closure, associativety and unique solutions) cause the set, having these properties, to be a  G R O U P.  In our case it is the symmetry group of the Equilateral Triangle.
A GROUP is a certain self-contained algebraic structure. It is a set of elements for which one binary operation is defined, such that the set is closed under this operation, and that this operation complies with the above mentioned conditions (associativity and unique solution). The latter conditions are called Group Axioms. From them a number of other properties can be deduced. For example, we can state that a GROUP always possesses one determined identity element (neutral element)  i. The latter can be defined as follows :

For every element of the GROUP the following holds :

In our case of the symmetry group of the Equilateral Triangle,  i  was the identity transformation, i.e. rotation of the triangle by 0⁰ (or 360⁰).

Also the following property of any GROUP can be deduced :

A GROUP always contains one determined inverse element, which here means that for every element  a  there is an inverse element a^-1, also belonging to the set, such that :

So because, for example (See our table),

b is the inverse of a and vice versa.
The inverse makes a transformation undone. In the case of a rotatation this means that we must rotate back with the same amount, effecting the net operation to be the identity operation.
In the case of undoing a reflection we must perform this same reflection again. Indeed, as can be seen in the above table,

in which c is a reflection with respect to the mirror line going through 1 of the above depicted triangle ( Figure 1 ). Indeed, if we flip (i.e. reflect) a figure and flip it again with respect to the same reflection line, then in fact nothing has happened : we have performed the identity transformation.

The symmetry group of the Equilateral Triangle is a so-called third-order Dihedral Group and is denoted in mathematics as D3. In crystallography it is called the Point Group 3m. It is called a point group because the involved symmetry transformations always leave at least one point where it initially was (In contrast with a translational symmetry transformation, where ALL the points are shifted to a new location).

Groups are thus very special sets of transformations, so the fact that the symmetries of an object form a group is a significant one.
We now know that every object inheres a set of rigid transformations that end up with the same object occupying the same space as before. They are covering transformations, symmetries, of the object. Such an object can be a two-dimensional motif. As such it has a point symmetry, described by a Point Group. In the previous documents we saw several such (two-dimensional) motifs having Point Groups 1, m, 2, 2mm, 4, 4mm, 3, 3m, 6 and 6mm. Only motifs possessing a point symmetry according to one of these ten Point Groups can figure in a translational two-dimensional array, i.e. can figure in a periodic pattern consisting of such a motif. But of course, when we do not demand the ability to figure in a periodic array, there can be objects with other point symmetries, for example a regular pentagon. The latter consists of 5 rotations (one of them is the identity transformation) and five reflections. It has a symmetry of 5m, and belongs to the fifth-order Dihedral Group, D5.
For three-dimensional motifs to be able to figure in a (three-dimensional) periodic array there are exactly 32 such motifs (i.e. motif symmetries), i.e. 32 Point Symmetry Groups (Point Groups). They represent the  32  3-D  Crystal Classes. In addition to these there are of course many other three-dimensional motifs (3-D objects) that cannot figure in a periodic array. They belong to other Point Groups.
In addition to the mentioned point symmetries there are  t r a n s l a t i o n a l  symmetries, namely in the mentioned periodic arrays. In a translational symmetry transformation ALL points are moved to a new location, and this is a fundamentally different kind of symmetry. So for example an infinite plane covered with square tiles (think of a bathroom wall). It indeed has those two quite different types of symmetry. First, you can select a particular tile, forming a Dihedral Group D4, just like the symmetries of a single square :   four rotations and four reflections. But there are also symmetries that move a given tile to some other tile. If the orientation does not change, these are  t r a n s l a t i o n s,  through a whole number of tiles horizontally and a whole number of tiles vertically. Because our infinite plane is covered with an infinity of such tiles, the product of the transformation that consists of a translation as just described, will precisely cover the original tiled plane, even though all points have moved to a new location. So such a translation is a genuine symmetry transformation. If we translate a tile (and translate the whole pattern) as described, and change the tile's orientation as well (and that of the whole pattern), such that the change in orientation is one of the possible rotations of the square (in which the rotated image covers the original exactly), then we have a combination of two symmetries, a translation and a rotation. Therefore every symmetry of the entire pattern of tiles is a combination of these two types (in which one of them or both can be the identity transformation : a zero translation and/or a zero rotation). The translations are called lattice symmetries or simple translations, and the individual D4's are Point Groups. Together they constitute (in our case) the Plane Group P4mm : The total symmetry of our tiled plane can be described by the repetition of motifs each having a point symmetry of 4mm (belonging to the Point Group 4mm, or equivalently, to the Dihedral Group D4), a repetition according to the Square Net with horizontal and vertical translation distances equal to a side of the tile (which is a square). The just mentioned repetition represents the pattern's translational symmetry.
In this particular pattern another symmetry is implied. It is also a translational symmetry, but of a different kind than the simple translations :   It is a combination of a reflection and a translation, which is called a  g l i d e   l i n e.  The corresponding transformation (which is a symmetry transformation and consequently such that the product -- the image -- covers the original entirely) is the following :   reflection across a line immediately followed by a translation parallel to that line over a certain distance. But in our case of the plane covered with square tiles this glide line (they occur in two directions perpendicular to each other) is just implied by the other symmeties of that tiled plane described earlier.
So when we take into account not only all point symmetry transformations, but also all translational symmetry transformations, we have to do with Plane Groups for two-dimensional patterns and Space Groups for three-dimensional patterns (in three-dimensional patterns we can, in addition to simple translation and glide planes, also encounter screw axes, which are a specific combination of a rotation and a translation).
There are exactly 17 Plane Groups for two-dimensional periodic patterns, and 230 Space Groups for three-dimensional periodic patterns.
Now we have enough knowledge to investigate some details concerning the relation between motifs in a periodic pattern and glide lines. This relation is important with respect to the derivation of the Complex Motif (Which in turn determines the planimetric (2-D) or stereometric (3-D) basic form of promorph of a given crystal).

Every crystal (also 2-dimensional crystals) has a  p e r i o d i c  structure, which means that a certain structural unit is regularly repeated without its orientation being changed. In principle no chinks are left, the given space is completely filled with these repeating units. In real crystals, however, these units have microscopical dimensions and are as such not visible in a crystal. The units are repeated in the directions of their edges with steps having the lengths of these edges : The latter represent the translation vectors according to which the units are repeated. Such a vector is called a simple translation. It is one of the symmetries of the given crystal, but it cannot as such be detected macroscopically. Its macroscopic (cumulative) effect, which indeed it has, consists in providing a  b u l k   a s p e c t  to the crystal.
In addition to these simple translations there often are other translation as well. They are combined with other symmetry elements, reflection and rotation, resulting in glide planes and screw axes respectively.
In two-dimensional crystals there can be no screw axes, but there can be  g l i d e   l i n e s.  Such a symmetry operation consists in a reflection across a line directly followed by a translation parallel to that line. In 3-D crystals also these translations (glide translations, screw translations) are of microscopical dimensions and cannot be detected macroscopically. By analogy they also cannot be detected in 2-D crystals (and also the simple translations cannot be so detected).
So the set of symmetries visibly present in crystals-as-macroscopic-objects do not involve translations. They only involve reflection, rotation and inversion. And these are transformations in which at least one point remains where it was. Because of this they are called point symmetries.
In translational symmetries, on the other hand, not any point remains where it originally was. The whole structure is  s h i f t e d,  but nevertheless will be mapped onto itself, i.e. the image of the operation covers the original pattern completely. Of course this can only be the case when the given structure is extended indefinitely in space. And because a crystal contains so many atoms, implying so many translation steps, it can reasonably be considered as infinitely extended in space. In other words, from the viewpoint of an atom in a crystal the array of atoms extends indefinitely in space. Analogously this is also the case in 2-D crystals.

As has been said, all crystals possess in addition to point symmetries -- point symmetry transformations -- translational symmetries, i.e. translational symmetry transformations. Taken them together, the set of point symmetry transformations plus translational symmetry transformations has the algebraic structure of a Plane Group for 2-D crystals, or of a Space Group for 3-D crystals. The operation of such a Group, i.e. the manipulation of its elements, which are the symmetry transformations composing the given set, is the successive execution of two such transformations, always resulting in a symmetry transformation already present in the set.
As we have done in the foregoing documents we concentrate on Plane Groups, i.e. on 2-D crystals (to pave the way for an understanding of 3-D crystals).
Of these 2-D crystals we endeavored to determine their tectological aspect, by means of the derivation of the Complex Motif. The latter determines the promorph or planimetric basic form of the given crystal.
To derive the Complex Motif we must strip the crystal structure of its periodic aspect. This we do by eliminating all translations inherent in that structure.
In 2-D crystals there are two types of translations, simple translations (which represent the periodic repetition of the structure's unit cell), and translations associated with glide lines. And of the latter there are again two types :   primary glide lines and implied glide lines.
An example of primary glide lines can be found in crystals of the Plane Group Pg. See for this Plane Group Part 4 of the present series of documents. There we considered a Pg pattern with space filling motifs. Here we shall briefly consider a Pg pattern in which the motifs are such that we can distinguish between the motif s.str. and its corresponding background. Although this background is (considered to be) featureless, it has a definite shape and size.

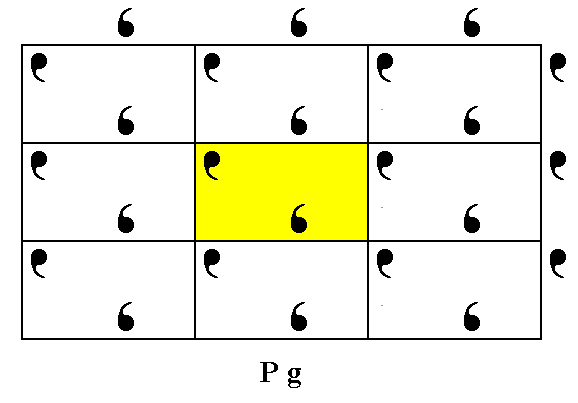
Figure 2. Asymmetric motifs (in fact motif units) placed in a primitive rectangular net, such that they alternate along the y edges (i.e. the horizontal edges) of the meshes, produce a pattern that represents the Plane Group Pg.
A unit cell is indicated (yellow).

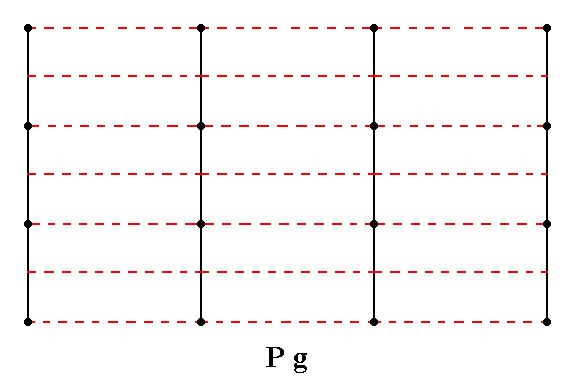
Figure 3. Total symmetry content of the Plane Group Pg.
Glide lines are indicated by red dashed lines. For clarity the nodes of the net are indicated (black dots).

Figure 4. Elimination of the glide translation by the Copy-Shift-Superimpose method. A repeat unit of the resulting pattern is indicated (yellow).

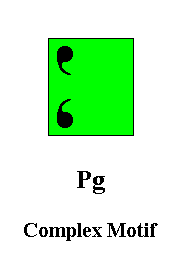
Figure 5. The repeat unit, as indicated in Figure 4, is isolated, yielding the Complex Motif of the Pg periodic pattern of Figure 2. The (point) symmetry of this Complex Motif is m.

A second type of glide line is a glide line that is implied by the other symmetries of the given pattern. It will not therefore be mentioned in the Plane Group Symbol. An example is the Plane Group P3m1. In such a pattern there is always a mirror line parallel to an existing glide line. And those mirror lines (one of each kind) will finally figure in the translation-free residue, and thus also in the Complex Motif. So in order to obtain the latter we do not need to transform such glide lines into mirror lines by eliminating their associated translations (glide translations), because mirror lines in the same direction are already present. We have shown this in the previous documents for all relevant Plane Groups. There we nevertheless eliminated those translations to see what happens. Indeed the symmetry did not further increase anymore, but the motifs became more crowded together. And this in fact means that we, in doing so, were already busy with eliminating the simple translations. When this process of eliminating the implied glide translation is continued (in a way that will be described shortly) the following will happen :
Insofar as the total motif is  compressible, which here means, insofar as the background of the motif s.str. (or of its units) is compressible, this background will shrink, until no compression is possible anymore (In 2-D crystals we think of analogues of atoms or atomic complexes). From that point on the crowding of the motifs will consist of  o v e r l a p p i n g s.   When the process is (conceptually) pursued till the limit, the centers of all motifs coincide, and the infinite structure has become finite. We have thus found the Complex Motif, and in this case the ultimate Complex Motif, as non-compressible translation-free residue of the initial periodic motif pattern.
We will demonstrate this with a pattern according to the Plane Group P3m1 :

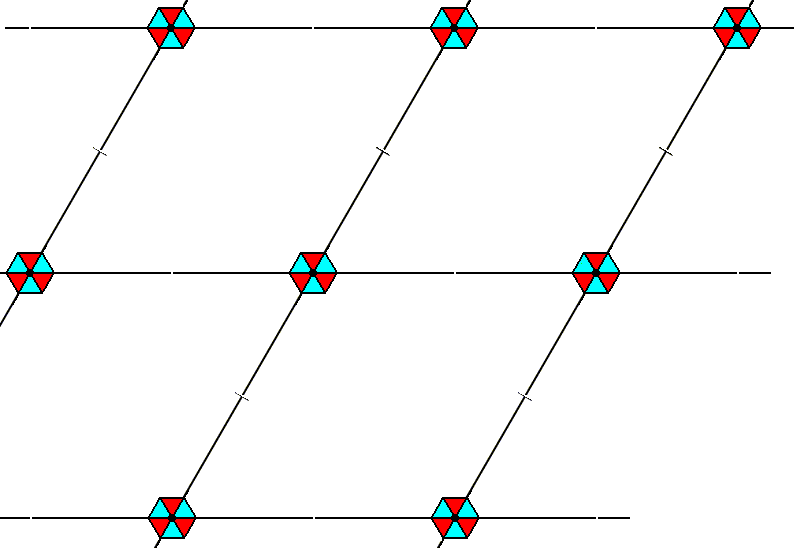
Figure 6. A periodic motif pattern according to the Plane Group P3m1. Each total motif consists of a tri-radiate motif s.str. plus corresponding background. The repeat is according to the Hexagonal Net (point lattice).

The next Figure indicates the corresponding background of each motif s.str.

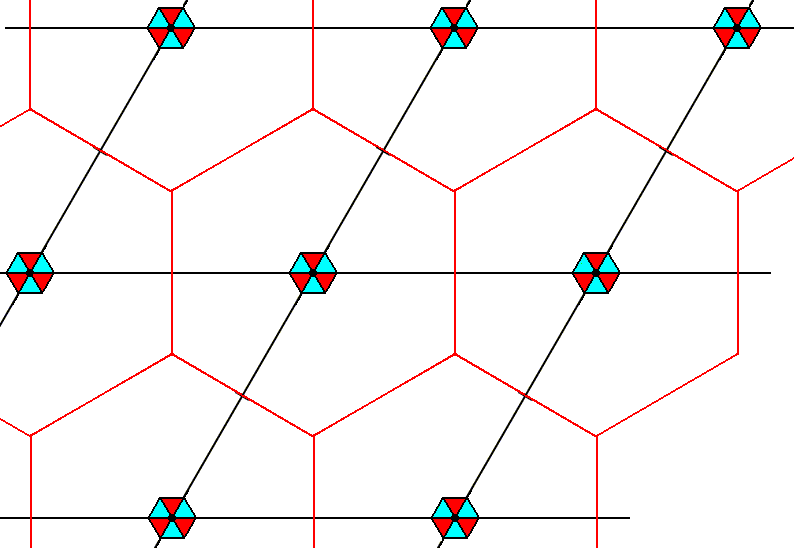
Figure 7. A periodic motif pattern according to the Plane Group P3m1. Each total motif consists of a tri-radiate motif s.str. plus corresponding background. The limits (boundaries) of these backgrounds are indicated. Their shape is hexagonal.

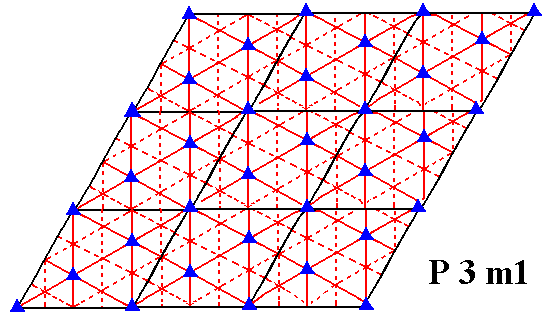
Figure 8.   Symmetry content of the Plane Group P3m1. Glide lines are indicated by dashed lines. Mirror lines are indicated by red solid lines, and the 3-fold rotation axes by small triangles.

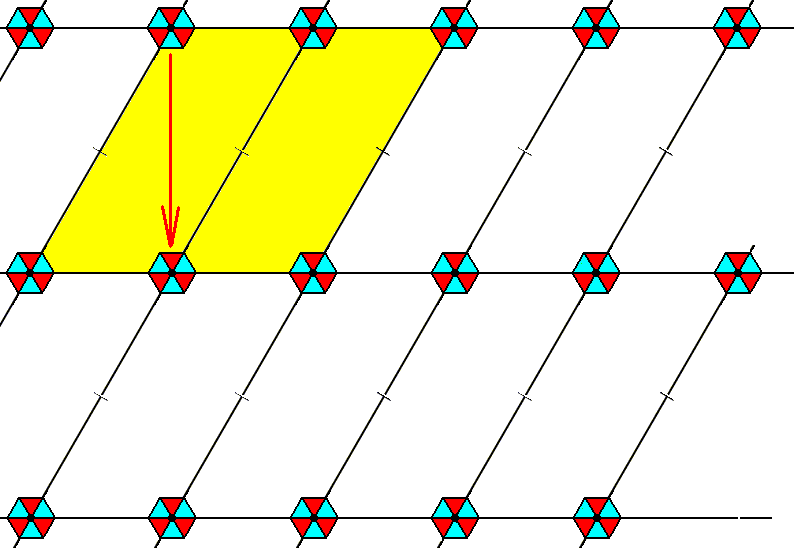
Figure 9.   Elimination of the vertical glide translation, by the Copy-Shift-Superimpose method. The shift is indicated by the red arrow.

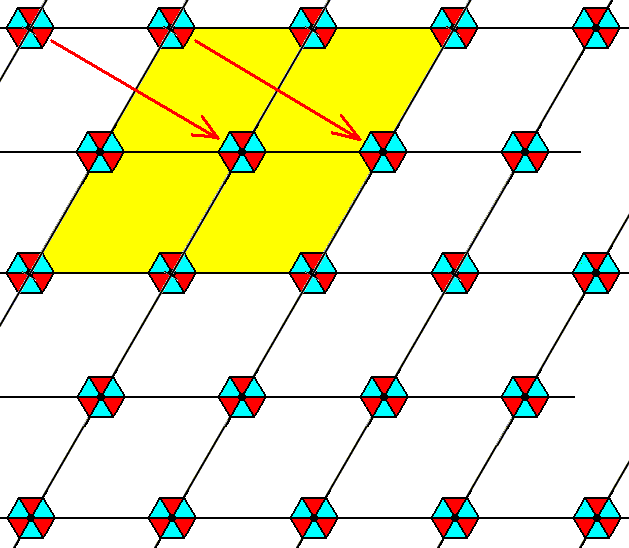
Figure 10.   Elimination of the glide translation normal to the non-horizontal unit cell edges, by the Copy-Shift-Superimpose method. The shift is indicated by the red arrows.

The next Figure shows this same result, but with the boundaries of the initial backgrounds (Figure 7) indicated.
As one can see, these boundaries pass through motifs s.str. So if we would interpret the crowding of the motifs, as effected by of the Copy-Shift-Superimpose operation, as an overlap of the corresponding (motif) backgrounds, then we would have motifs.str. that were at the same time background, which is evidently impossible. Therefore we must interpret the crowding of motifs as a compression of the backgrounds.

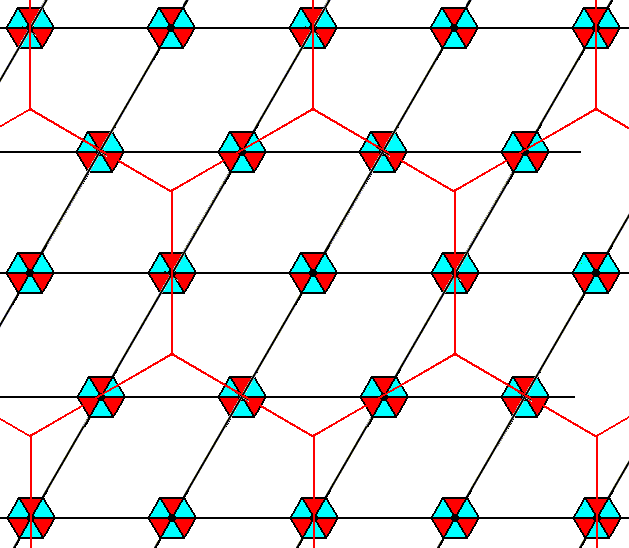
Figure 11.   In the result of Figure 10 the old background boundaries are indicated. They turn out to pass right through motifs s.str. which would mean that such a motif s.str. would be at the same time a background, which is impossible. The crowding of motifs s.str. must accordingly be interpreted as a compression of those backgrounds.

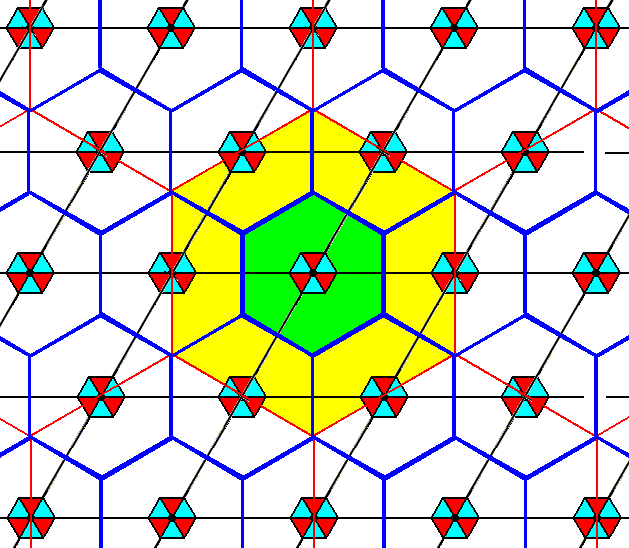
Figure 12.   In the result of Figure 10 the new backgrounds -- the boundaries of which are indicated by haevy blue hexagons -- of the motifs s.str. are indicated, and compared with the old ones. The old backgrounds have been considerably compressed. Together with its corresponding motif s.str. such a background is a true repeat unit.

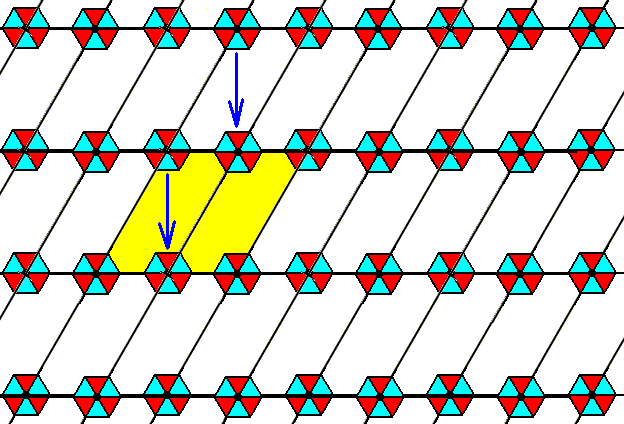
Figure 13.   The vertical glide translation inherent in the pattern of the Figures 10, 11 and 12, is undone. In the next Figure all remaining glide translations are eliminated.

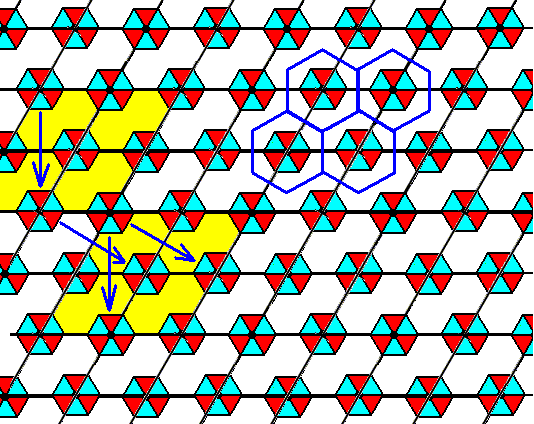
Figure 14.   The other glide translation, perpendicular to the non-horizontal unit cell edges, is eliminated, implying the elimination of all remaining glide translations. The effect is a still smaller scale version of the pattern of Figure 6, i.e. yet smaller again than what it was in Figure 11. The distance between the centers of the motifs (s.str.) has become correspondingly smaller.

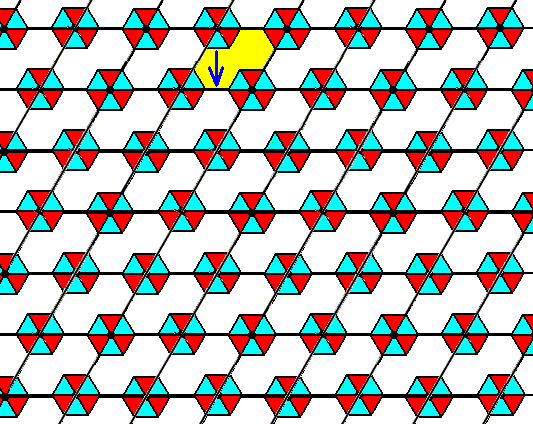
Figure 15.   Undoing of vertical glide translations in the pattern of Figure 14. The result is shown in the next Figure.

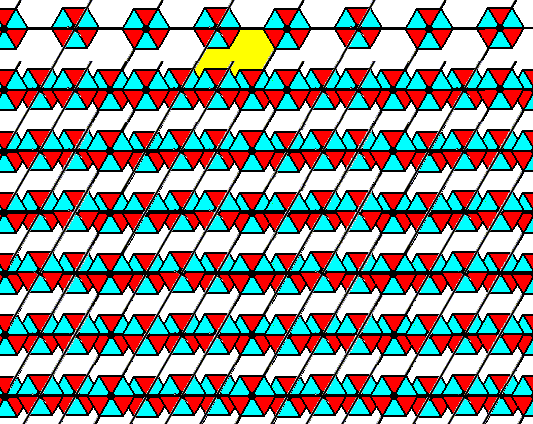
Figure 16.   Vertical glide translations in the pattern of Figure 14 eliminated.

Figure 17.   The glide translations (in the pattern of Figure 14) perpendicular to the non-horizontal unit cell edges are eliminated. With them all remaining glide translations (as they are present in the pattern of Figure 14, with their proper translation distances) are eliminated. The result shows that  o v e r l a p  of motifs s.str. is beginning to take place.

Figure 18.   The non-compressible residue or ultimate Complex Motif of the periodic P3m1 motif pattern of Figure 6. It consists of a motif s.str. plus some (non-compressible) background.

In the next document we will investigate these matters in the case of EXTENDED MOTIFS, i.e. periodic (2-D) patterns consisting of motifs that, at least at first sight, fill their background completely, which means that such motifs are contiguous, and that there is in principle no distinction between a (non-contiguous) motif s.str. and its background.

e-mail :  lovelace@hetnet.nl

back to homepage

back to the seventeenth part of the Preparation to the Promorphology of Crystals