Stereometric Basic Forms of Inorganic Beings
On the elimination of glide translations (Sequel)
e-mail :  lovelace@hetnet.nl

Extended Motifs

Extended motifs fill their backgound completely (or almost completely), implying that the whole total motif is structured everywhere (or almost everywhere) within its confines. It is in immediate contact with the neighboring motifs, which means that there is structural continuity all along the lattice lines. The fact that the motifs do not interpenetrate, and thus not (further) compress, can be seen as the result of short-range repulsive forces that set in when the motifs come close to each other. The overlap process which then sets in when we eliminate the simple translations is conceptual in its nature, but the result is concrete :   It is a chemical motif which as such is tectological in its nature, i.e. aperiodic.
In Part XVII, of the Series of documents which consider the derivation of the Complex Motif with respect to all the 17 Plane Groups, we discussed, with respect to the Plane Group P6mm, (1) the case of extended motifs which are considered to be wholly rigid, (2) the case of extended motifs which are partly compressible, and, finally (3) the case of motifs s.str. coming together as their structureless backgrounds shrink.
The second case -- extended motifs that are partly compressible -- presupposes a motif consisting of very small parts, that are homogeneously present in a structureless matrix. That's why such a motif could be compressed to a certain extend.
We will now consider the case of extended motifs composed of large parts heterogeneously situated in a compressible matrix. Also in this case the structured aspect, though interrupted in some places, reaches the boundary of the total motif, and is as such contiguous with the structural aspect of the neighboring total motifs. The next Figure depicts a schematized version of such a motif.

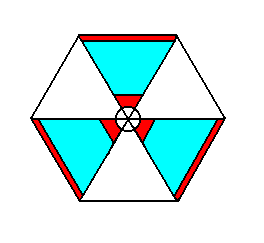
Figure 1.  A partly compressible motif compatible with a hexagonal point lattice. The red bands symbolize the large parts of structure of which the motif is composed. These parts are not radially compressible. The blue parts on the other hand, are compressible, and especially radially compressible, because they are supposed to be composed of very small structural elements more or less homogeneously embedded in a compressible matrix. The center of the motif is considered to be not compressible at all.
So we presuppose that the center of the motif is not at all shrinkabe while the red parts of the motif are radially incompressible. The white parts are fully compressible, while the blue parts are partly compressible because they are supposed to consist of small non-compressible elements in a compressible matrix.
If we tile the plane with such a motif we get the following P31m periodic pattern.

Figure 2.  P31m pattern consisting of a periodic repetition of the motif of Figure 1.
The next Figure indicates a rhomb-shaped unit cell. We can verify that the structure is according to Plane Group P31m.

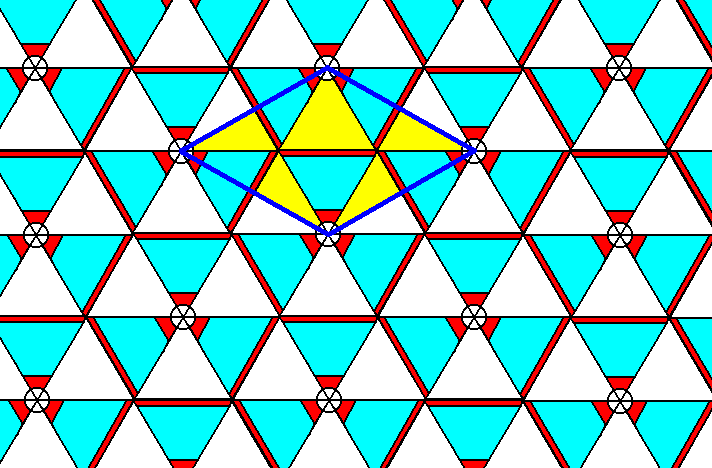
Figure 3.  P31m pattern consisting of a periodic repetition of the motif of Figure 1.
A rhomb-shaped unit cell is indicated.
The next two Figures indicate the elimination of the glide translations inherent in the pattern of Figures 2 and 3. For this the Copy-Shift-Superimpose method is used. Only the centers of the motifs are shown.

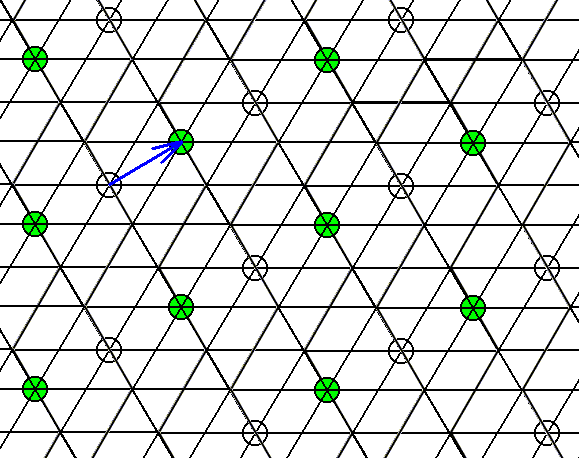
Figure 4.  Elimination of the glide translation parallel to one of the edges of the unit cell, shown by the centers of the motifs.

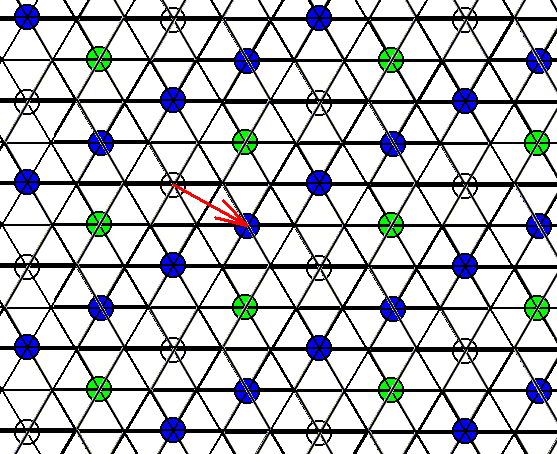
Figure 5.  Elimination of the glide translation parallel to the other edge of the unit cell, implying the elimination of all remaining glide translations, originally present. Shown by the centers of the motifs.
After some processing the pattern -- represented by just the centers and boundaries of the motifs -- looks like this :

Figure 6.  The resulting pattern after elimination of all glide translations originally present. Only the centers and the boundaries of the motifs are shown. The outlines of four total motifs are indicated.
The next Figure shows the effect of the compression -- which itself is a result of the above elimination of all glide translations originally present -- on the motif. The compressed motif is compared with the original motif.

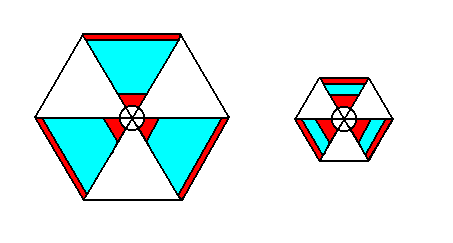
Figure 7. 
Left image :  Original motif
Right image :  Compressed motif.
The white and blue parts are compressed. The red parts are not (radially) compressed.
Figure 6 and 7, and their derivation, show the compression of the motifs, in contrast with non-compressible (extended) motifs. But their purpose is not just to show compression, but to illustrate a case of partial compression in virtue of the presence of non-compressible features within the motif. As an example, a non-compressibility of some parts of the motif in the radial direction is chosen :  The red parts of the motif are radially not compressible, so their width (in the radial direction) remains the same after compression of the motif, i.e. a shrinking of the motif in virtue of the compression takes place in other (than radial) directions and in any case in other parts (areas) of the motif.

The pattern consisting of a repetition of this compressed motif (i.e. pattern according to Figure 6, but now provided with the details of the motifs) is depicted in the next Figure.

Figure 8.  Tiling of the plane with the compressed motif of Figure 7 (right image).
This pattern is the same as was obtained earlier, in Figure 6. In Figure 6 it was obtained by the elimination of all glide translations of the p31m pattern of Figure 2 and 3. This elimination caused the crowding of the extended motifs, resulting in their compression.
In Figure 8 we can see that the typical glide translations of a P31m pattern are still present. But in the form in which they were present in the original pattern (Figure 3), they are not present anymore. Their scale has changed. The translations involved are only half as long as they were in the original pattern.
When we continue the process of shrinking by yet another application of the Copy-Shift-Superimpose operation with half the shift length as was applied before, radial compression cannot take place any further because the radial width of the blue (compressible) areas is too small, so the result will be the beginning of overlap. In the limit of this precess the motifs, as they are in Figure 8, will coincide, resulting in one motif only, which is then the ultimate Complex Motif of the pattern of Figure 3 (and, of course also of Figure 2).

With all what has been said in this and the previous document, we have concluded our further elaboration of the process of the elimination of glide translations.
We can now go back to where we were in the document treating of the Complex Motif of P6mm periodic patterns, accessible by the second LINK below.
e-mail :  lovelace@hetnet.nl

back to homepage

back to the seventeenth part of the Preparation to the Promorphology of Crystals

 

back to the beginning of the present consideration concerning the elimination of glide translations