
back to homepage
The External Shapes of periodic 2-D arrays of repeated two-dimensional motifs
We continue our investigation concerning the faces, Forms and combinations of Forms in two-dimensional crystals.
Hexagonal Net (continued).
In the previous Part we concluded the exposition of 2-D crystals belonging to the Class 3m and representing the Plane Group P3m1.
Now we will treat of the second (and last) Plane Group, P31m, of that Class.
Let us first depict a pattern (as given earlier in this series of Parts) that represents this Plane Group.
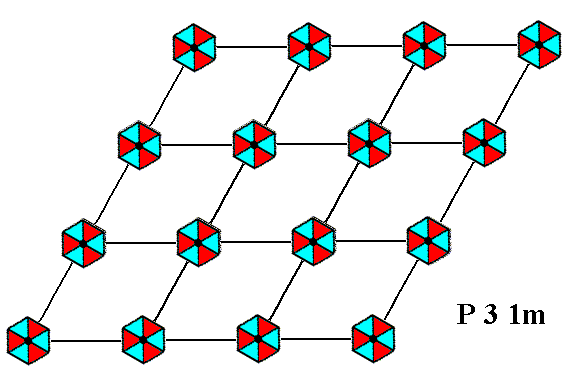
Figure 1. A pattern of periodically repeated motifs representing Plane Group P31m . The pattern is the same as that of Figure 8 in Part Seventeen (Plane Group P3m1), but now its motifs are rotated 300 with respect to the net and to the system of crystallographic axes. The hexagonal net is drawn such that it can be seen as composed of rhomb-shaped building blocks.
In the next Figure we depict this same pattern, but now using a smaller mesh. Moreover we have inserted NW--SE lines in order to visualize hexagonal building blocks.
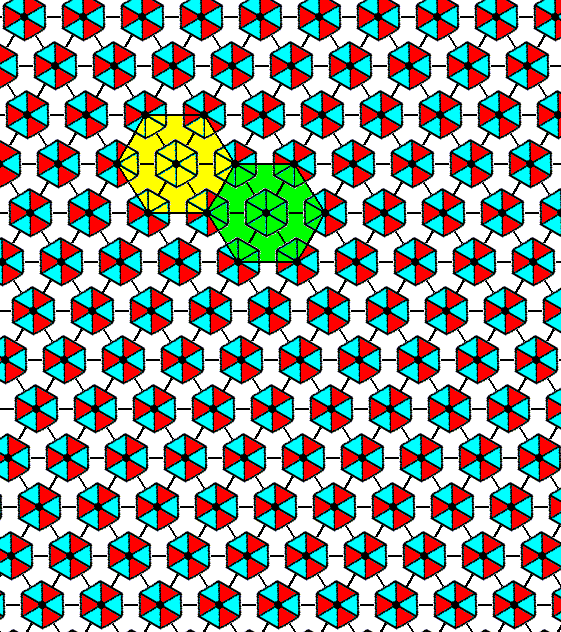
Figure 2. A periodic pattern of motifs representing Plane Group P31m . The repetition of the motifs is still according to a hexagonal net, now using smaller meshes, and having inserted diagonal NW--SE lines in order to indicate h e x a g o n a l building blocks (two of them highlighted).
The motif pattern, for example as we see it in Figure 2, demands a different orientation of the three mirror lines (as a result of the motifs being rotated with respect to those of the previous Plane Group). The three mirror lines now coincide with the three crystallographic axes.
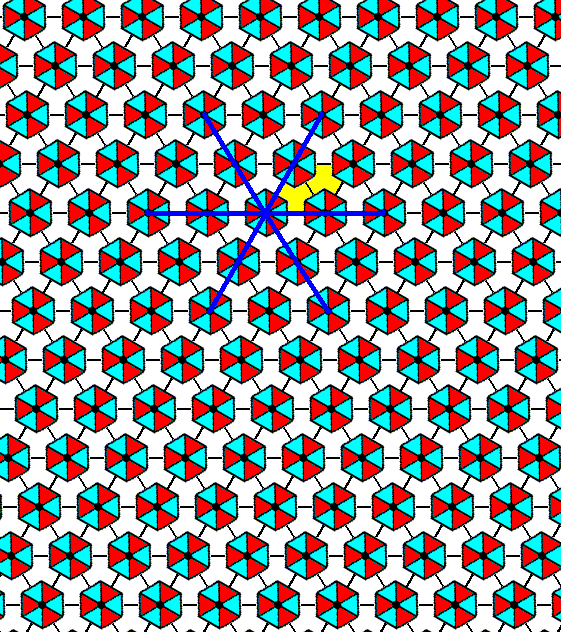
Figure 3. Orientation of the three mirror lines (blue) as demanded by the motif pattern representing Plane Group P31m . The mirror lines coincide with the three crystallographic axes. The latter are still such that two axes go along the edges of the rhomb-shaped unit mesh (yellow).
Because of this we must again derive the Forms of the Class, but of course these Forms will have the same shapes as the ones derived earlier, because the same symmetry content is involved in both cases. Only their orientations with respect to the system of crystallographic axes differ.
Introducing a face parallel to one of the crystallographic axes results in a multiplication by 6, in virtue of the actions of the mirror lines (now coincident with the axes). The 3-fold rotational symmetry is then implied. See the next Figure.
Figure 4. When an intial face, parallel to one of the crystallographic axes, is subjected to the symmetry elements of the present Class (3m), five new faces are generated, making up a closed Form that has the shape of a regular hexagon. As such it can represent a crystal of this Class (See the next Figure).
Figure 5. A two-dimensional crystal of the Class 3m . It has the same shape as the one depicted in Figure 3 in Part Seventeen, but its orientation with respect to the crystallographic axes differs.
Introducing a face, perpendicular to one of the crystallographic axes (and so by implication perpendicular to one of the mirror lines) results in its multiplication by 3, in virtue of the 3-fold rotation axis. The mirror lines do not multiply these faces further, so the result is a closed Form having the shape of an equilateral triangle. See the next Figure.
Figure 6. When an initial face, perpendicular to one of the crystallographic axes (which are coincident with the three mirror lines), is subjected to the symmetry elements of the present Class, two more faces are generated, together making up a closed Form having the shape of an equilateral triangle. This triangle can represent a crystal of the present Class ( See Figure 7).
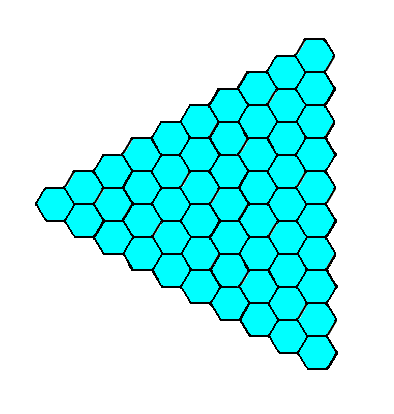
Figure 7. A two-dimensional crystal of the Class 3m of the 2-D Hexagonal Crystal System. It has the same shape as the one depicted in Figure 5 in Part Seventeen, but its orientation with respect to the system of crystallographic axes is different.
Introducing yet another possible face, namely one that is neither perpendicular nor parallel to one of the crystallographic axes leads to five more faces in virtue of the symmetry elements of our Class. See the next Figures.
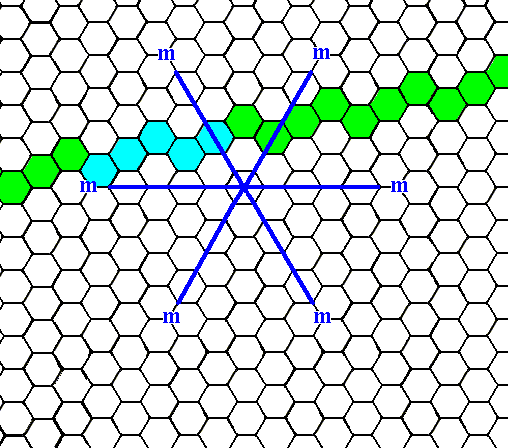
Figure 7a. An initial face that is neither perpendicular nor parallel to one of the crystallographic axes. We will concentrate on the blue part of it.
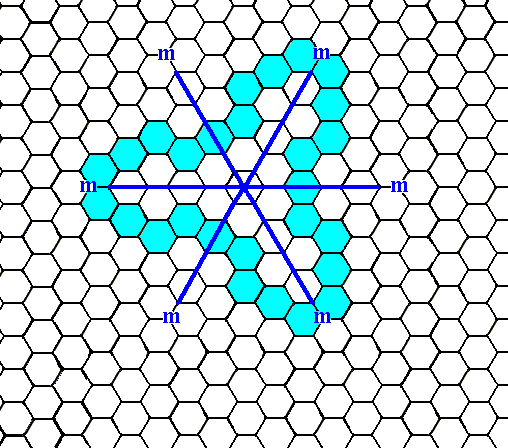
Figure 7b. When an initial face, as specified above, is subjected to the symmetry elements of the present Class (3m), five more faces will be generated. The resulting (closed) Form, however, turns out to have receding angles (The figure, as can be seen, is indented). It cannot, therefore, represent a crystal (because of energetic reasons). So we must look for a face that is as general -- with respect to its orientation -- as this one, but not causing receding angles. Such a face is depicted in the next Figure.
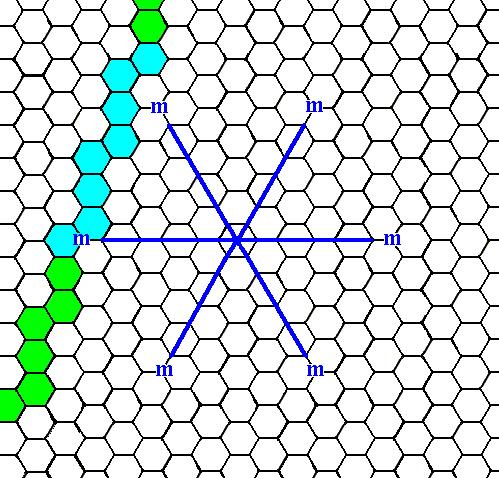
Figure 7c. An initial face that is neither parallel nor perpendicular to any of the crystallographic axes, but with a different orientation than the one in Figure 7a.
From the face given in Figure 7c we now will derive the Form, by subjecting it to the symmetry elements of our Class (3m). See the next Figures.
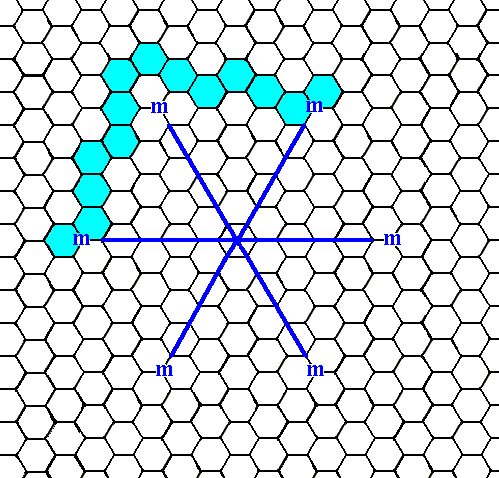
Figure 7d. When the initial face, as specified above (Figure 7c), is subjected to the symmetry elements of the present Class, a ditrigonal Figure will be the result, a figure without receding angles. Here only the first stage of this generation is shown : The initial face is reflected in a mirror line (as one of the symmetry elements of our Class), resulting in two faces that are symmetrically situated with respect to the mirror line.
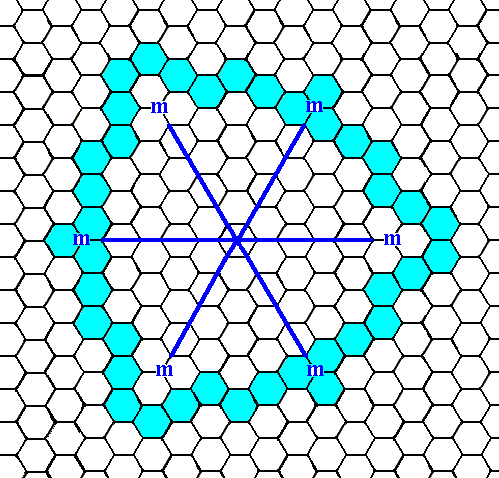
Figure 7e. When the initial face, as specified above, is introduced, the actions of the mirror lines will generate five more faces (The 3-fold rotation axis is then implied), resulting in a closed Form having the shape of a ditrigon, i.e. a six-sided figure with equal sides but with alternating angles. As can be seen there are no receding angles present. This closed Form can represent a crystal of our Class (See next Figure).
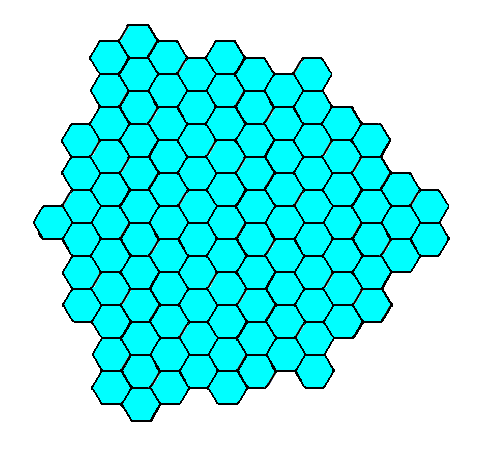
Figure 7f. A two-dimensional crystal of the Class 3m of the 2-D Hexagonal Crystal System.
Its ditrigonal shape is emphasized in the next Figure.
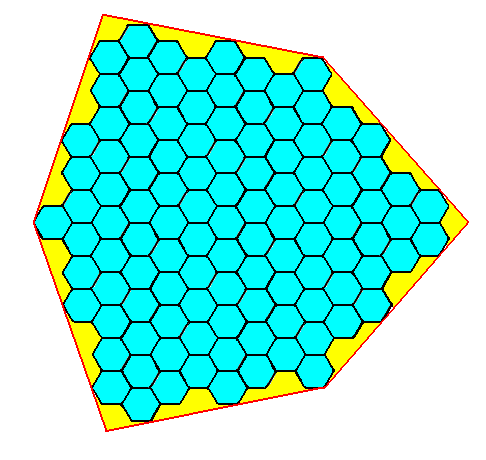
Figure 7g. The same as Figure 7f, but now with emphasis on the ditrigonal shape of the crystal.
We can now study the atomic aspects presented to the growing environment by the faces and Forms of our Class (3m). In our case the orientation and symmetry of the motifs is such that we have to do with a pattern that represents Plane Group P31m.
Figure 8. Indication -- but not yet a full construction -- of the atomic aspect presented to the environment by the top face of the Form depicted in the Figures 4 and 5.
The next Figure completes the construction of the atomic aspect.
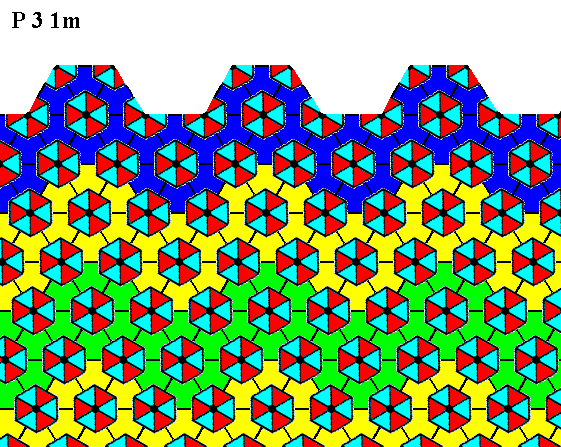
Figure 9. Atomic aspect presented to the environment of the face specified above.
The incomplete motifs indicate unsatisfied or distorted chemical valences.
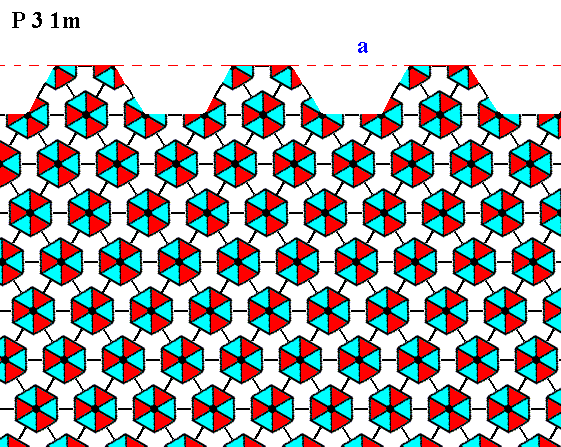
Figure 10. The same as Figure 9, but now with some coloration omitted in order to highlight the motifs. The face is indicated by a .
In the above Figures it can clearly be seen -- when we inspect the motifs, i.e. their coloration, representing different structural units -- that there is no mirror line anywhere perpendicular to the face, although the external shape of the crystal (Figure 5) suggests such a mirror line going through the center of each face. So the morphological symmetry of the crystal is higher than the crystallographic symmetry.

Figure 11. Indication -- but not yet a full construction -- of the atomic aspect presented to the environment by the lower right face of the Form depicted in the Figures 4 and 5.
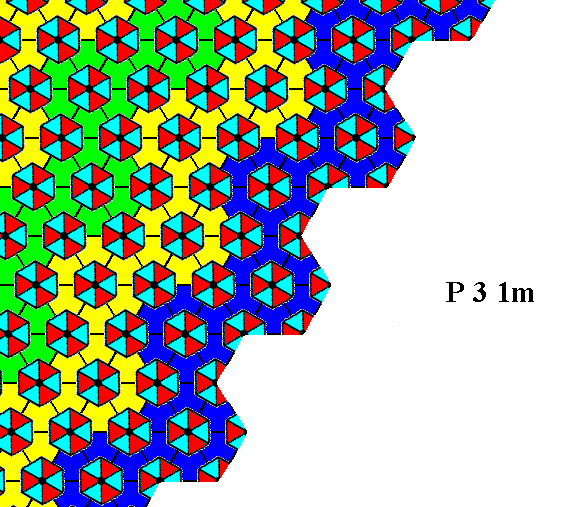
Figure 12. Atomic aspect presented to the environment by the face specified above.
Incomplete motifs represent unsatisfied or distorted chemical valences.
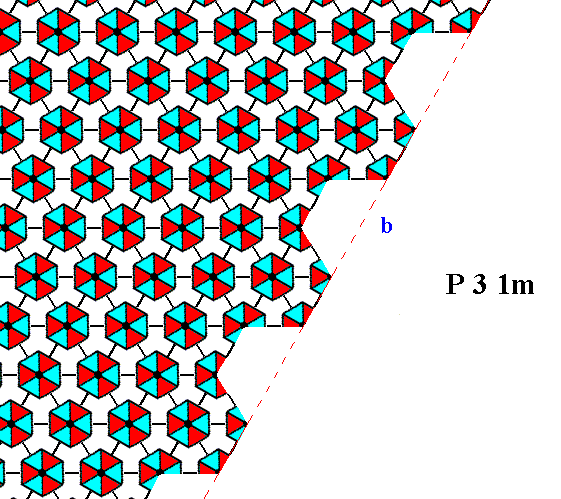
Figure 13. The same as Figure 12, but now with some coloration omitted in order to highlight the motifs. The face is indicated by b.
The face in the above Figures is equivalent to the one in the Figures 8, 9 and 10. And indeed we also here (i.e. in the Figures 11, 12 and 13) see that there is no mirror line anywhere perpendicular to the face, although the external shape of the crystal (Figure 5) suggests such a mirror line (one perpendicular to each face, resulting in three such mirror lines).
The next Figures depict the atomic aspects presented to the growing environment by the faces of the second Form of our Class as derived above (Figures 6 and 7).

Figure 14. Indication -- not yet a full construction -- of the atomic aspect presented to the environment by the right face of the Form depicted in the Figures 6 and 7.
The Class is 3m , and the Plane Group is P31m .

Figure 15. Atomic aspect of the face specified above.
The incomplete motifs indicate unsatisfied or distorted chemical valences.
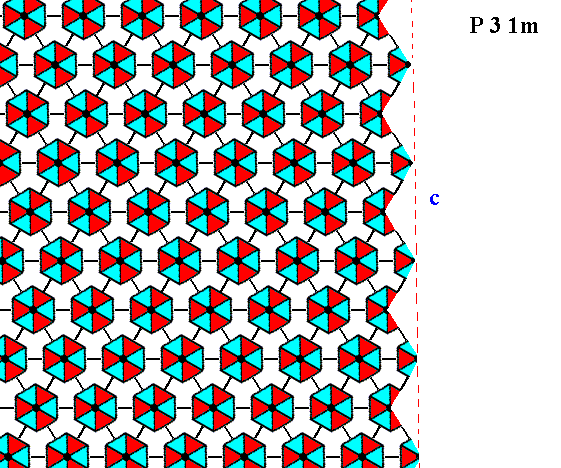
Figure 16. The same as Figure 15, but now with some coloration omitted in order to highlight the motifs. The face is indicated by c.
The atomic aspect presented to the growing environment by the face depicted in Figure 7c (which, together with its equivalents, is also given in the Figures 7d, 7e, and 7f), is constructed in the next Figures.

Figure 17. Indication -- not yet a full construction -- of the atomic aspect presented to the environment by the face specified above. The Class is 3m , and the Plane Group is P31m .
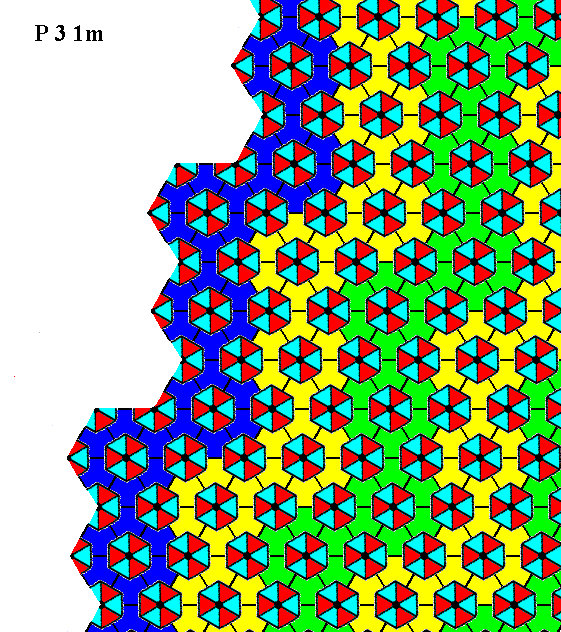
Figure 18. Atomic aspect presented to the environment by the face specified above.
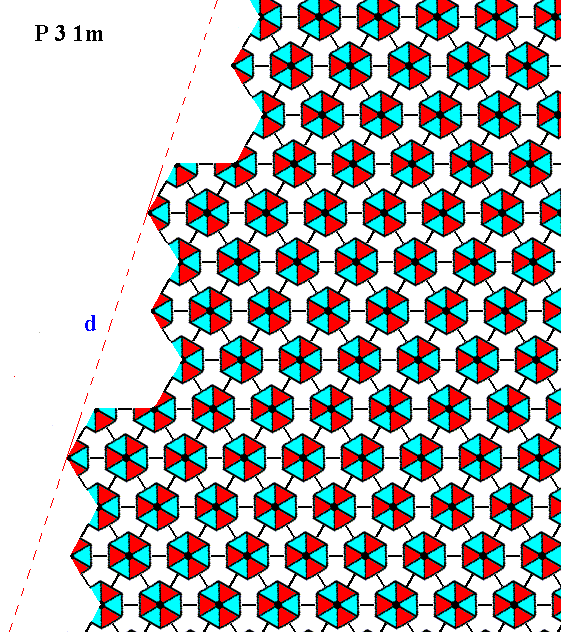
Figure 19. The same as Figure 18, but now with some coloration removed in order to highlight the motifs.
Incomplete motifs indicate unsatisfied or distorted chemical valences. The face is indicated by d.
This concludes our exposition of the atomic aspects connected with the Plane Group P31m, and with it our exposition of the Class 3m of the 2-D Hexagonal Crystal System.
In the next Part we will continue with the remaining Classes of the System, namely the Classes 6 and 6mm.
To continue, click HERE for Part Nineteen.
back to homepage