back to homepage
The symmetry of regular 2-D arrays of repeated motifs (continued)
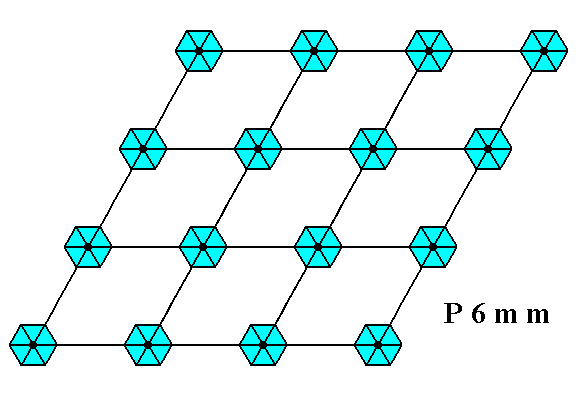
Placing two-dimensional motifs with 6mm symmetry into a (primitive) hexagonal net (2-D hexagonal lattice), yields a periodic pattern representing Plane Group P6mm. See Figure 1.

Figure 1. When motifs, having point symmetry 6mm (i.e. having a 6-fold rotation axis and two types of mirror lines), are inserted into a (primitive) hexagonal net, a pattern of repeated motifs will emerge that represents Plane Group P6mm.
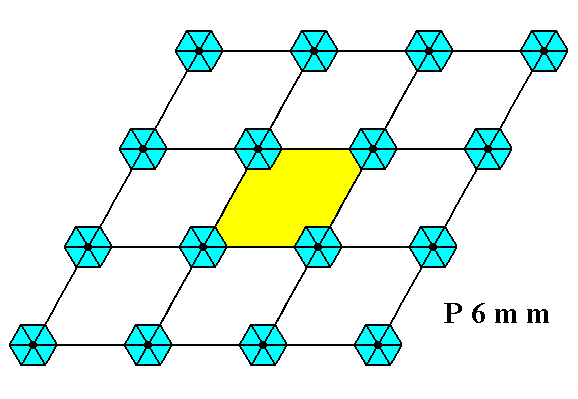
Figure 1a. A unit mesh is chosen (yellow). This unit mesh is primitive, and its point symmetry is 2mm.
If the pattern representing Plane Group P6mm is contracted such that all translations are eliminated, then we end up with a figure that has 6mm symmetry. It is the translation-free residue of that Plane Group, and as such represents the Point Group to which that Plane Group belongs. See Figure 1b.
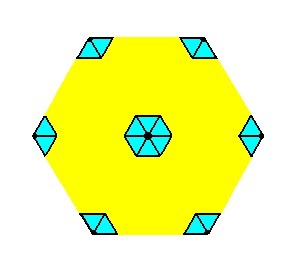
Figure 1b. The translation-free residue of the Plane Group P6mm.
The symmetry of this residue is 6mm, i.e. it has a 6-fold rotation axis going through its center and perpendicular to the plane of the drawing, three mirror lines, each connecting two opposite corners, and three mirror lines connecting the centers of opposite edges.
The translation-free residue is, in the present case, also the motif s.l., which means that as such it tiles the 2-D plane completely, as the next Figure shows.
Figure 1c. Tiling of the two-dimensional plane by the motif s.l. of the pattern of Figure 1.
The symmetries involved in patterns representing Plane Group P6mm are simple translations, glide lines, mirror lines, 6-fold, 3-fold and 2-fold rotation axes. Some of these symmetries are shown in the next Figures.
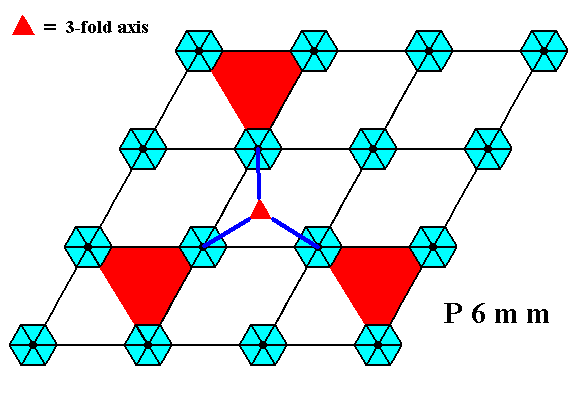
Figure 1d. A pattern representing Plane Group P6mm has 3-fold rotation axes.
One of them is shown.
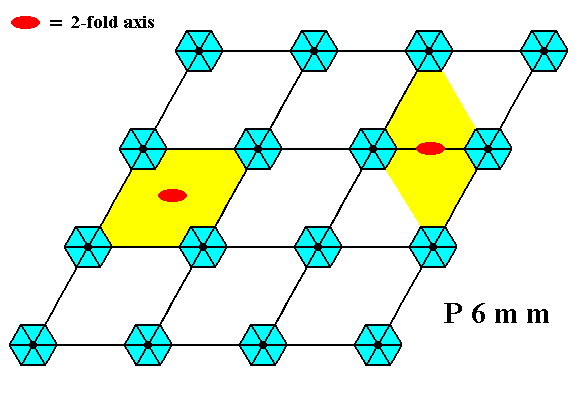
Figure 1e. A pattern representing Plane Group P6mm has 2-fold rotation axes.
Two of them are shown.
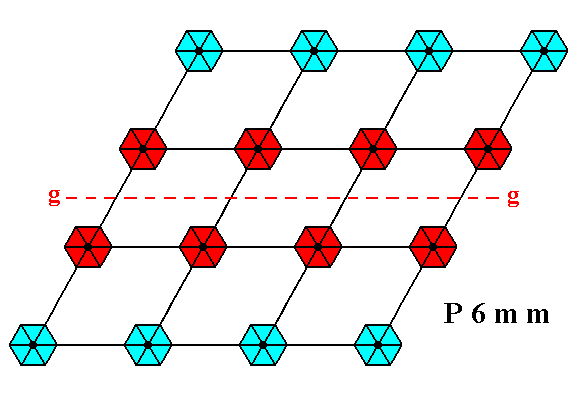
Figure 1f. A pattern representing Plane Group P6mm has glide lines.
One of them is shown.
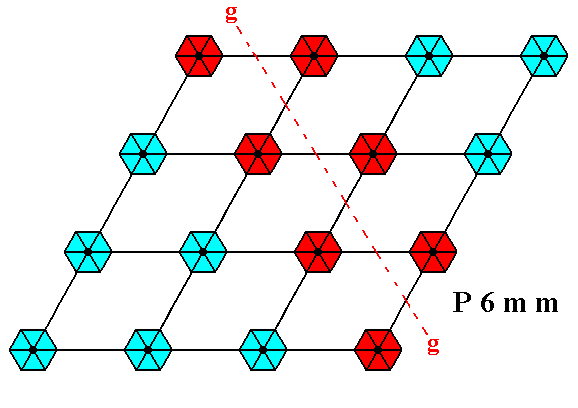
Figure 1g. A pattern representing Plane Group P6mm has glide lines.
Again, one of them is shown.
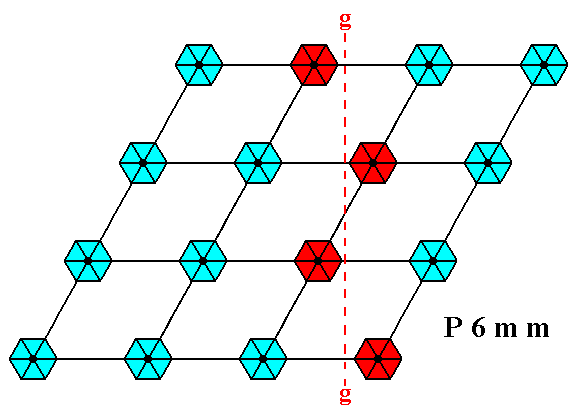
Figure 1h. A pattern representing Plane Group P6mm has glide lines.
Again, one of them is shown.
The total symmetry content of Plane Group P6mm is depicted in Figure 1i.
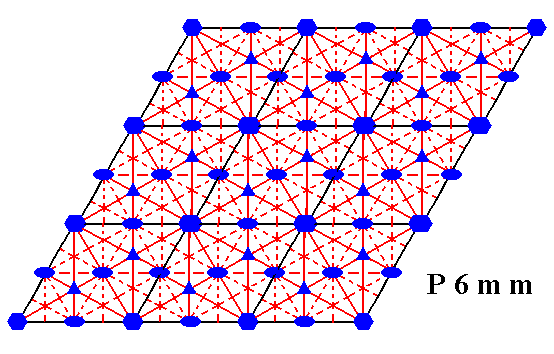
Figure 1i. Total symmetry content of the Plane Group P6mm.
All rotation axes are perpendicular to the plane of the drawing.
6-fold rotation axes are indicated by small blue solid hexagons.
3-fold rotation axes are indicated by small blue solid triangles.
2-fold rotation axes are indicated by small blue solid ellipses.
Glide lines are indicated by red dashed lines.
Mirror lines are indicated by solid lines (red and black).
(One should not worry about the small discrepancies at some places in the drawing.)
So we have found the (only) Plane Group (P6mm) belonging to Class (Point Group) 6mm of the 2-D Hexagonal Crystal System.
Next we will consider the Class 6.
Placing motifs with point symmetry 6, i.e. motifs having only a 6-fold rotation axis, into a hexagonal net, such that the motifs are associated with the lattice nodes, yields a repeating pattern representing Plane Group P6. See Figure 2.
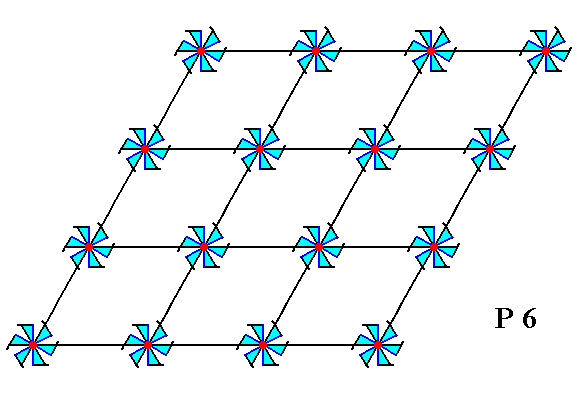
Figure 2. Inserting motifs with point symmetry 6 into a 2-D hexagonal lattice, yields a periodic pattern representing Plane Group P6.
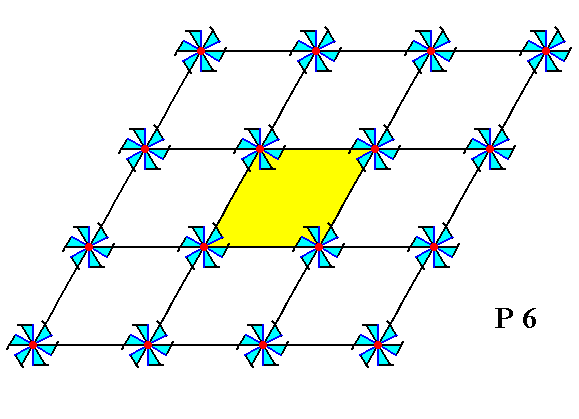
Figure 2a. A unit mesh is chosen (yellow). This unit mesh has a point symmetry 2, and is primitive.
If the pattern representing Plane Group P6 is contracted such that all translations are eliminated, then we end up with a figure that has 6 symmetry. It is the translation-free residue of that Plane Group, and as such represents the Point Group to which that Plane Group belongs. See Figure 2b.
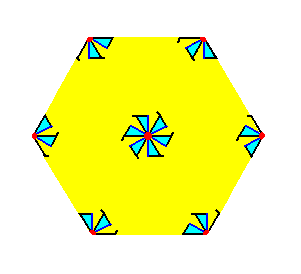
Figure 2b. The translation-free residue of the Plane Group P6.
The symmetry of this residue is 6, i.e. it has, as its only symmetry element, a 6-fold rotation axis going through its center and perpendicular to the plane of the drawing.
The translation-free residue is, in the present case, also the motif s.l., which means that as such it tiles the 2-D plane completely, just like the translation-free residue of the pattern of Figure 1.
A pattern representing Plane Group P6 has no mirror lines and also no glide lines. The distribution of rotation axes is, however, exactly the same as in Plane Group P6mm. See Figure 2c for the total symmetry content of Plane Group P6.
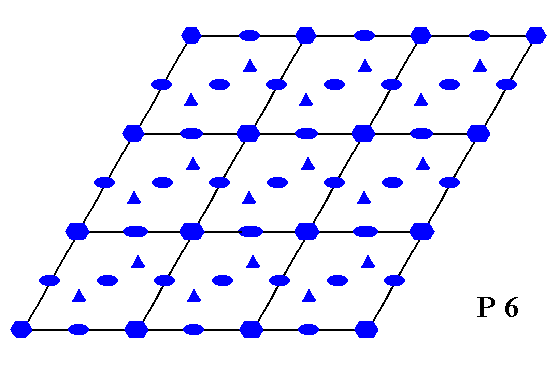
Figure 2c. Total symmetry content of Plane Group P6.
So we have found the (only) Plane Group (P6) belonging to Class (Point Group) 6 of the 2-D Hexagonal Crystal System.
Two distinct Plane Groups, P3m1 and P31m, belong to Point Group 3m. They have the same total symmetry content and shape, but the motifs differ in orientation with respect to the edges of the unit mesh. Let's start with Plane Group P3m1.
Placing motifs into a hexagonal net, but now motifs, having a point symmetry 3m -- meaning that each motif has a 3-fold rotation axis going through its center (and perpendicular to the plane of the drawing), and three equivalent mirror lines, such that their point of intersection coincides with the center of such a motif -- and oriented in the net such that their mirror lines do not coincide with the connecting lines of the net, yields a pattern (of repeated motifs) representing Plane Group P3m1. See Figure 3.
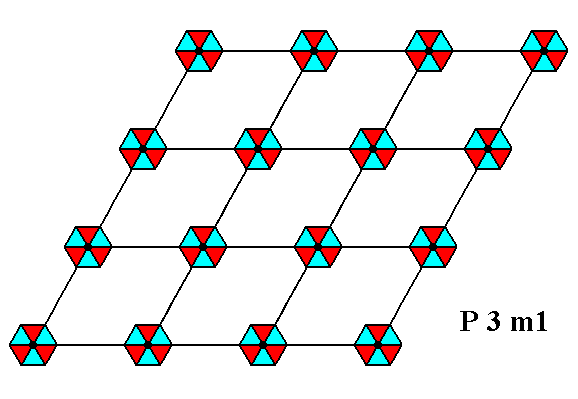
Figure 3. The insertion of motifs having 3m symmetry and oriented as described above, into a hexagonal net, leads to a periodic pattern representing Plane Group P3m1.
The symmetry of the motifs is indicated by their shape and by their coloration.
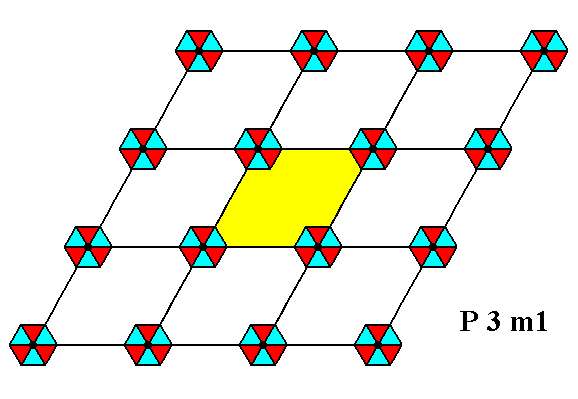
Figure 3a. A unit mesh is chosen (yellow). It is primitive, and its point symmetry is m , meaning that its only symmetry element is a mirror line.
If the pattern representing Plane Group P3m1 is contracted such that all translations are eliminated, then we end up with a figure that has 3m symmetry. It is the translation-free residue of that Plane Group, and as such represents the Point Group to which that Plane Group belongs. See Figure 3b.
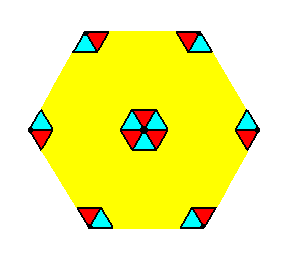
Figure 3b. The translation-free residue of the Plane Group P3m1.
The symmetry of this residue is 3m, i.e. it has a 3-fold rotation axis going through its center and perpendicular to the plane of the drawing, and three equivalent mirror lines.
The translation-free residue is, in the present case, also the motif s.l., which means that as such it tiles the 2-D plane completely, just like the translation-free residue of the pattern of Figure 1 (See (click) Figure 1c).
The symmetries involved in a pattern representing Plane Group P3m1 are 3-fold rotation axes, mirror lines and glide lines. See Figures 3c, 3d, 3e and 3f.
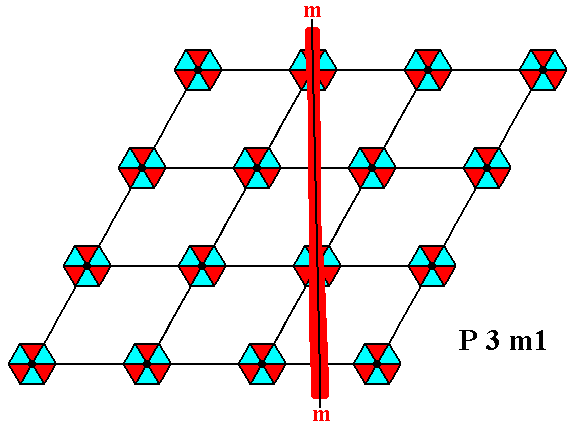
Figure 3c. A pattern representing Plane Group P3m1 has mirror lines. One of them is indicated.
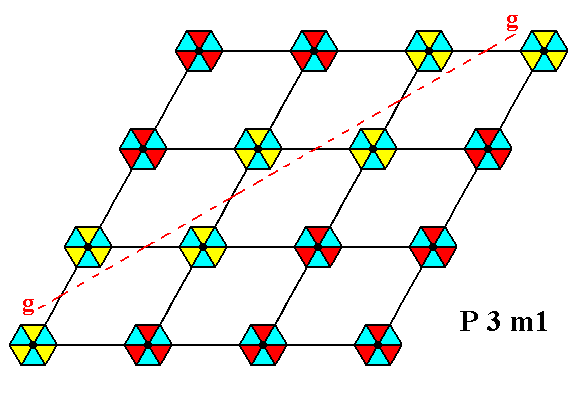
Figure 3d. A pattern representing Plane Group P3m1 has glide lines. One of them is indicated.
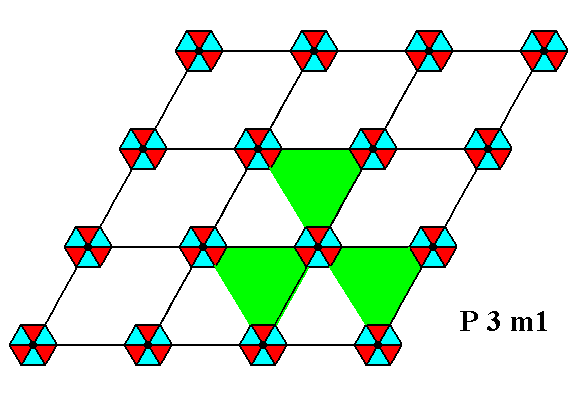
Figure 3e. A pattern representing Plane Group P3m1 has 3-fold rotation axes perpendicular to the plane of the drawing. One of them is indicated.
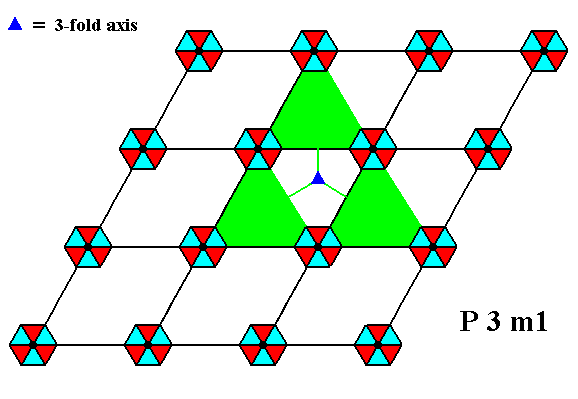
Figure 3f. A pattern representing Plane Group P3m1 has 3-fold rotation axes perpendicular to the plane of the drawing. Again one of them is indicated (small blue triangle).
The total symmetry content of the Plane Group P3m1 is depicted in the next Figure.
Figure 3g. Total symmetry content of the Plane Group P3m1.
3-fold axes are indicated by small solid blue triangles.
Glide lines are indicated by dashed red lines.
Mirror lines are indicated by solid red lines.
For clarity we depict this same total symmetry content, but now referring only to one mesh of the net :
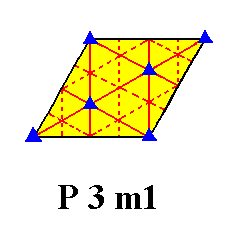
Figure 3h. Total symmetry content of Plane Group P3m1, depicted for one mesh of the net. Only the red solid lines are mirror lines.
The second, and last, Plane Group belonging to the Class 3m will be discussed in the next Part.
To continue, click HERE for Part Six.
back to homepage