

back to homepage
Introduction
In previous documents of this website we have concentrated on the external (i.e. macroscopically visible) symmetry features of crystals. We have derived the thirty-two Crystal Classes based on these features (See the document on Derivation (Parts I -- VI)), and we have derived all the possible Forms -- A Form is a set of equivalent crystal faces consistent with the symmetry content of the Class to which that Form belongs, i.e. this set makes up a figure having the symmetry of the Class -- of each Crystal Class (See the introductory document on Crystal Morphology, and all the documents on the (six) Crystal Systems, beginning with the Isometric Crystal System). A real crystal can be represented by a single such Form provided that the latter is a closed Form (i.e. when it encloses a part of space completely). A real crystal can also be represented by a combination of Forms -- but only a combination of Forms belonging to the same Crystal Class, i.e. having the same symmetry content -- which means that individual crystals often show many faces. Such a combination can involve closed as well as open Forms, as long as the result is a closed configuration of faces. These combinations, or single closed Forms, determine the final (intrinsic) shape of a crystal individual, and we want to know -- i.e. not only to describe -- why crystals of a certain substance exhibit certain definite combinations of Forms, and why some Forms tend to dominate over other Forms in one and the same combination. This has to do with the different rates of growth of the different crystal faces (and, consequently, of the different Forms). We know that these growth rates are dependent on the chemical composition of the crystal and on its internal ordering. Chemical composition and internal ordering imply the existence of different aspects of the crystal surface to the growing environment, i.e. possible different faces can present different aspects to the growing environment. We can call the chemical composition + internal ordering the internal structure of the crystal.
How do we know about the existence in crystals of internal structure? Why couldn't all matter be just a structureless jelly?
There are two discoveries that led to this idea of matter having some sort of fine structure (Recall that most solid mattter is crystalline).
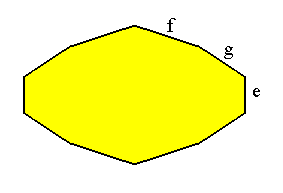
Figure A1. Cross section of crystal, showing the faces e, g and f. The symmetry of the crystal indicates that we will find these three faces, with their angles between them, four times around the crystal.
We can measure the angle between e and g, and between e and f (and then we also know the angle between f and g).
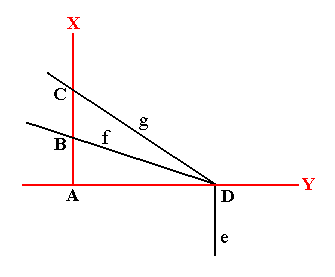
Figure A2. The faces f and g intersect the line X at the points B and C, while face e is parallel to line X.
Lines X and Y are perpendicular to each other.
When we measure the lengths of AB and of AC we will find that AC is exactly twice as long as AB. The existence of this simple relation between the interfacial angles suggests that these angles can be constructed by regularly stacking one and the same type of buildingblock that has sides in the same proportion as (the proportion of) AD to AC. See Figure A3.
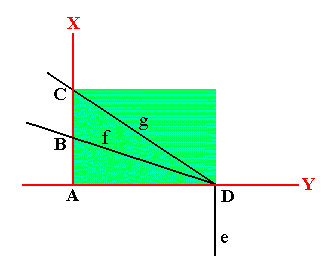
Figure A3. A building block (green) can be stacked in a regular fashion to construct the angles between the faces e, f and g, and by implication the whole crystal can be build from a regular stacking of that same building block.
The next Figure shows how the regular stacking of building blocks with sides having the same proportion as AD : AC supports the three angles and consequently the three faces e, f and g.
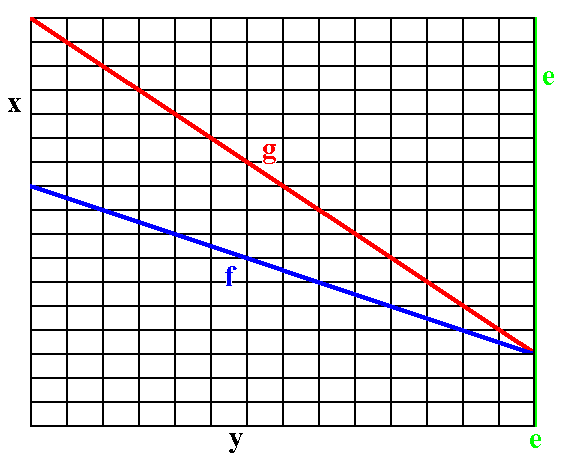
Figure A4. The faces e (green), f (blue) and g (red) can be constructed by the regular stacking of building blocks, each of them having the lengths of its sides in the same proportion as the lengths of AD and AC in Figure A3.
The next two Figures show how the faces g and f are formed by the stacking of the building blocks. Of course those building blocks are imagined to be of microscopical dimensions, causing the faces to be smooth macroscopically.
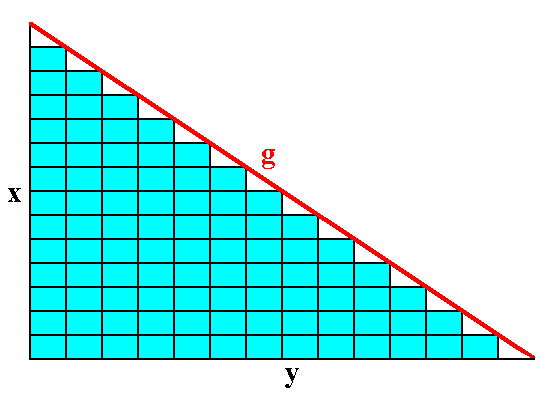
Figure A5. The face g can be constructed by the stacking of the building blocks.
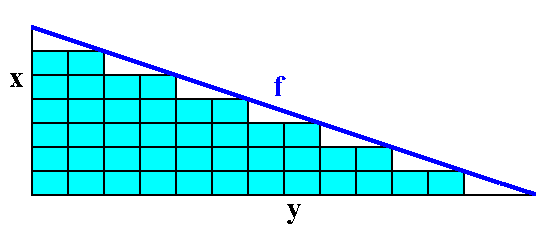
Figure A6. The face f can be constructed by the stacking of the building blocks.
The face e can of course be constructed by the same stacking of those building blocks : It can be traced out along a vertical series of the shorter side of them (See Figure A4).
We can now form a crystal (section) consisting of three (sorts of) faces making the same angles with each other as the faces e, g and f considered above. See Figure A7.
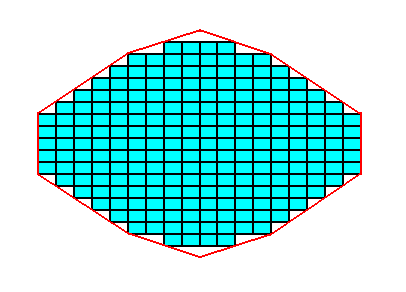
Figure A7. A section of a crystal is constructed from building blocks having the same ratio of their sides as the ones constructed and used above.
What we have found here for two dimensions (namely for a section through a crystal) can easily be exended to a three-dimensional case.
In the same way we can proceed with crystals of other substances. And indeed, one has never found one for which a suitable building block could not be chosen. A crystal turns out to be made from the regular stacking of a building block (without turning it while stacking) having certain proportions of the length of its edges. Many crystals exhibit a great wealth of faces, but always a single shape of building block can account for all the faces. All the relations such as that of AC to AB in Figure A2 turn out to be simple : The ratios of the corresponding lengths (also) in all other cases are simple fractions. Any face can be made by stepping back just a few blocks after piling up just a few rows. Of course only the shape of such building blocks is considered here. In fact only their contents matters. This contents is an atom, ion or a small group formed from them (generally we can call it a motif or motif cluster), and this contents is regularly repeated in three dimensions. To visualize the repetition of such an atom or group of atoms is to imagine a regular box or cell in which they are placed. This cell (building block), and its contents, is then repeated in a regular fashion resulting in the crystal.
So a crystal is a homogeneous solid possessing, long range, three-dimensional internal order. Such order is the result of the repetition of a motif ( These are chemical units, for instance Iron atoms) by regular translations (i.e. shifts along straight lines) in three dimensions. The 3-dimensional pattern is said to be homogeneous if the angles and distances from one motif to surrounding motifs in one location of the pattern are the same in all parts of the pattern.
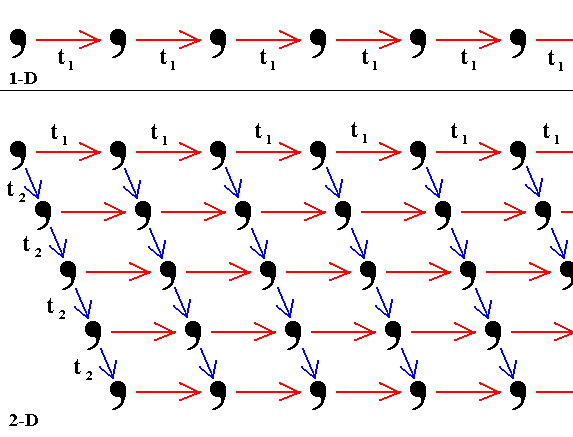
Figure 1.
Top image : Translation by a vector t1 of a motif (represented by a comma), over and over again, results in an infinite one-dimensional periodic pattern.
Bottom image : Translation of this one-dimensional periodic pattern over and over again by the vector t2 results in an infinite two-dimensional periodic pattern.
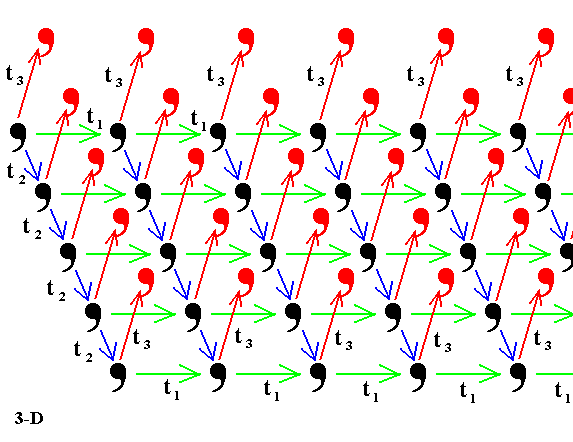
Figure 2. When a two-dimensional periodic pattern is translated by a vector t3 not lying in its plane, over and over again (in the Figure only one such translation is shown), an infinite three-dimensional periodic array results (For reasons of clarity the added motifs are colored red).
It is often convenient to ignore the actual shape of the motifs in a pattern and to concentrate only on the geometry of the repetitions in space. If the motifs are replaced by points, we have a regularly pattern of points that is referred to as a lattice
A lattice is, therefore, an imaginary pattern of points (or nodes) in which every point (node) has an environment that is identical to that of any other point (node) in the pattern. A lattice has no specific origin (a 'beginning'), as it can be shifted parallel to itself.
In order to fully understand the three-dimensional lattices on which the structure of crystals is based, and (to understand) the assignment of motifs to these 3-D lattices (i.e. the replacement of their points (nodes) by motifs, having a certain shape), let us first develop two-dimensional lattices, and see how they can be provided with two-dimensional motifs, generating in this way two-dimensional imaginary crystals. When all this is done we'll turn our attention again to real, i.e. three-dimensional, crystals. The reason for this approach is the following :
Because we are not going to tackle the problem of understanding the structure of three-dimensional crystals by means of a rigorous mathematical approach in terms of symmetry theory (in Mathematics this will involve the Theory of Groups), but by means of a more or less morphological approach -- this, in order to be able to make a smooth transition to the understanding of the structure of Organisms -- it is absolutely necessary first to consider the structure of two-dimensional crystals. They will provide us with most of the basics for an understanding of the structure of three-dimensional crystals. In fact what we're going to undertake is a complete two-dimensional crystallography (along morphological lines), and this will take twenty of the Parts on the internal structure of crystals (The rest of the present Part, and Part II -- XX). Only after these Parts we will direct our attention to three-dimensional crystals, i.e. to real crystals.
Remark : We've just said that we will not rigorously derive the internal structure of three-dimensional crystals. In fact, however, we will let the reader choose among both possibilities : the mathematical, i.e. group theoretic approach and the morphological approach. The latter approach is, in a way, less appropriate for dealing with the understanding of the internal structure of three-dimensional crystals, because drawings intended to illustrate this structure will become messy and unclear (This in contradistinction to drawings depicting the internal structure of two-dimensional (imaginary) crystals). So with respect to three-dimensional crystals, we are in fact forced to follow the other approach, the group theoretic approach. We have done so in the sequel to this website, which technically is a second website, accessible by the following link : Continuation of this Series (This link can also be found at the bottom of the left frame).
This mathematical approach starts with a series of documents that introduces Group Theory, with extra emphasis on the symmetry groups of two- and three-dimensional geometric Figures and also of two-dimensional periodic patterns (which can represent the internal structure of two-dimensional (imaginary) crystals). After that we use group theory to create a systematic exposition of all the symmetries of three-dimensional crystals (including their point symmetries -- point groups -- as well as their total symmetry, i.e. including their translational symmetries). In this whole approach, although being mathematical, we will not aspire to present all this in full mathematical rigor, but nevertheless with enough rigor to serve our purposes.
But, because we can understand that not every reader is willing to study the fairly long series of documents on group theory and its application to Crystallography (and to the study of the basic stereometric forms of organisms -- Promorphology, also laid down on the second website), we will do our best to make it nevertheless possible for those readers to gain an understanding of the internal structure of three-dimensional crystals, without studying group theory. For such an understanding the present and following documents on the internal structure of two-dimensional crystals is of paramount importance. If these are studied carefully, then one certainly obtains some insight into the three-dimensional case without studying group theory.
The present and following documents are about two-dimensional crystals. Such crystals involve precisely 10 point groups and 17 plane groups. So, in a way, groups are involved anyway, but not so much in a group theoretic context. We could say that the two-dimensional patterns, involved in two-dimensional crystals, are representations of the corresponding groups (which are the main mathematical entities in group theory), and these representations are examined analytically, which means that the mentioned patterns are as such given, and what we do is to examine the symmetries inherent in those patterns.
In the mentioned group theoretic approach those patterns will be (moreover) studied from a synthetic point of view, which means that such a pattern, and with it the corresponding group, will be generated by one or more basic motifs (representing symmetry transformations and therefore representing group elements) from some one initial motif (representing the identity element of the relevant group). This synthetic group theoretic approach will yield much insight in those patterns and paves the way for an understanding of three-dimensional patterns as we see them in real crystals.
Two-dimensional lattices (Plane Lattices)
Intuitive derivation of the five Plane Lattices (nets).
Crystals are of a translative periodic nature. So their internal structure must have this translative character, i.e. this structure must be based upon a lattice.
Likewise their 2-D analogues. Thus a 2-D lattice not only should tile the 2-D space exhaustively (i.e. without left-over spaces), it must also be translative : The 'tiles' must be repeated periodically in two directions, implying that the sides of the tiles must be two by two parallel.
There are five, and only five, possible unique types of plane lattices, or nets (See Figures below). These types are distinguished from each other by the equality or non-equality of the sides of the individual repeated unit (unit mesh), which could serve to be a building block of a particular lattice, and by the angle gamma obtaining between the two non-parallel translation directions, a and b of such a net. This angle gamma can either be special, namely 900, 1200 (or 600), or such that cos (gamma) = a / 2b (The latter angle is such that a rectangular net is produced that is centered, i.e. having also a lattice point in the center of each rectangle),
or be general, i.e. the angle gamma is neither 900, nor 600, nor 1200 nor such that
cos (gamma) = a / 2b (An angle of 450 implies angles of 900, so it does not need to be considered).
Equal sides imply rhomb-shaped tiles with angles of 1200 (or 600), or square tiles with angles of 900.
Unequal sides imply rectangular tiles, or tiles having the shape of a parallelogram. This parallelogram is either such that cos (gamma) = a / 2b, or a parallelogram with general angles (not 900, not 600, not 1200).
Where the tile is a rhombus we have a hexagonal net : There the smallest repeated unit is a rhombus. A larger repeated unit is a (centered) hexagon. We will see that -- concerning the hexagonal net -- this hexagon can be chosen as the preferred building block.
These five nets include four fundamentally different shapes :
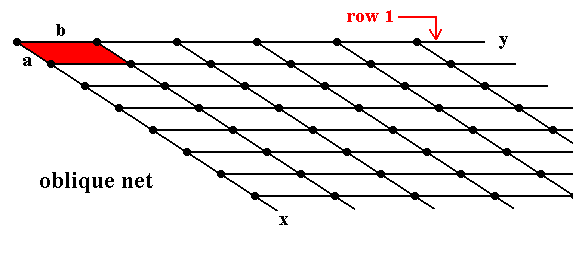
Figure 3. Oblique Net (Clinonet).
a is not equal to b.
gamma is not 900.
Row 1 (the upper row of nodes) is (in its entirety) indefinitely repeated by translations along direction x with translation distance a .
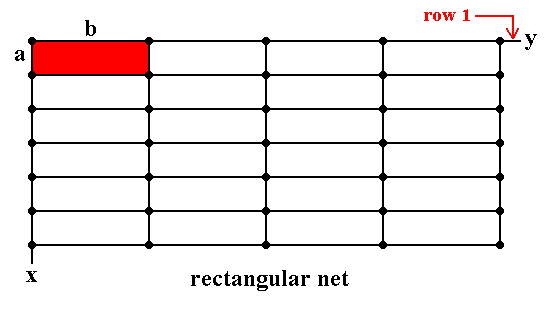
Figure 4. Rectangular Net (Orthonet).
a is not equal to b.
gamma is 900.
Row 1 (the upper row of nodes) is (in its entirety) indefinitely repeated by translations along direction x with translation distance a .
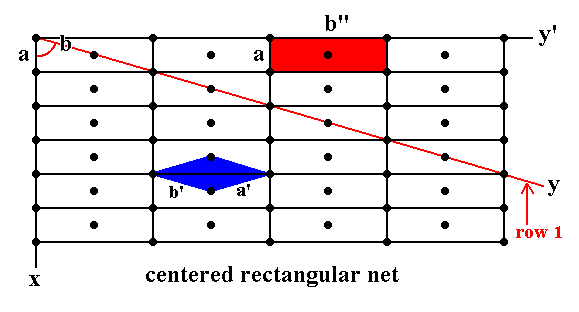
Figure 5. Centered Rectangular Net (centered Orthonet) (= Diamond Net).
a is not equal to b ( b is measured from the 'origin' of the net along the y direction until the first node).
gamma ( i.e. the angle between the x direction and the y direction) is such that
cos (gamma) = a / 2b.
Row 1 (the nodes along the red line) is (in its entirety) indefinitely repeated by translations along direction x with translation distance a. A centered unit mesh choice is given in red.
Another choice of unit mesh is given in blue. This is a primitive mesh with a' = b', gamma* ( i.e. the obtuse angle between a' and b' ) is not equal to 900, 600 or 1200. Because of the possibility of this (diamond shaped) unit mesh choice, the net is also called Diamond Net.
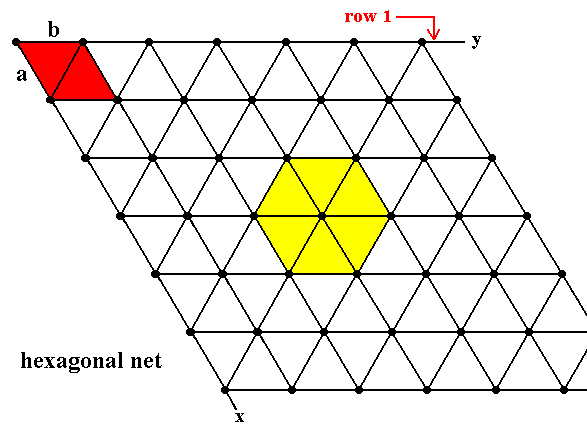
Figure 6. Hexagonal Net (Hexanet).
a is equal to b.
The angle gamma between the x direction and the y direction is 600.
Row 1 is indefinitely repeated by translations along direction x with translation distance a . The smallest unit mesh choice is indicated in red (it is a rhombus).
Another (larger, and centered) unit mesh choice is indicated in yellow.
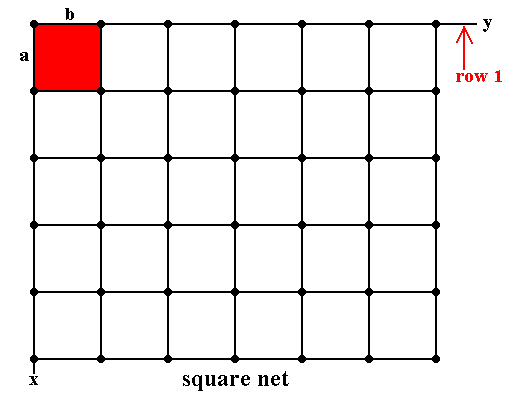
Figure 7. Square Net (Tetranet).
a = b, gamma = 900.
Row 1 is indefinitely repeated by translations along direction x with translation distance a . The unit mesh choice is indicated in red.
If we place motifs in such a net, such that each motif is associated with a lattice node -- note that the environment of a motif s.str. also belongs to the motif (s.l.) -- then we get
Derivation of the 10 two-dimensional Crystal Classes (2-D Point Groups)
In Part One of the series of documents on The Derivation of the 32 Crystal Classes (Section Derivation of the possible rotational symmetries in Crystals) we proved that in any periodic array the only rotational symmetries that can occur are 1, 2, 3, 4 and 6. In two dimensions horizontal rotation axes, as well as inversion, are not possible. Mirrors -- mirror lines -- are of course possible. From these data we can now derive all the possible 2-D Crystal Classes (Planar Point Groups). This means that we are going to derive all possible combinations of the symmetry elements 1, 2, 3, 4, 6 and m. The symmetry elements may each be taken individually or may be combined to produce all the two-dimensional Point Groups.
So from the outset we have already the following 2-D Point Groups (= 2-D Crystal Classes) :
1, 2, 3, 4 and 6.
Addition of a mirror line to the symmetry content of Class 1 yields Class m (Which is equivalent to 1m). See Figure 8.
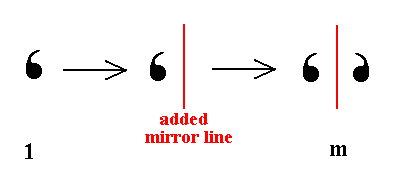
Figure 8. Derivation of the Class m from Class 1 by adding a mirror line.
Addition of a mirror line to the symmetry content of Class 2 yields Class 2mm. See Figure 9.
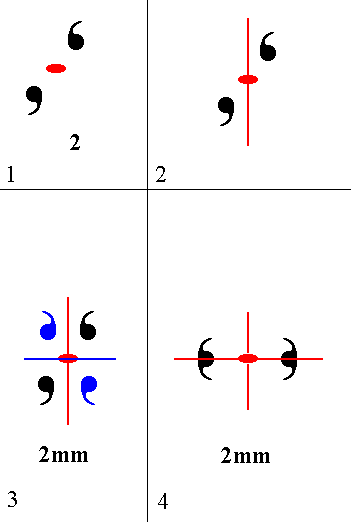 |
Figure 9.
Derivation of Class 2mm from Class 2. (1). Motif pattern consistent with Class 2. The 2-fold rotation axis, perpendicular to the plane of the drawing (in fact it is a 2-fold rotation point, because we have to do with a 2-D pattern), is indicated by a small solid red ellipse. (2). Addition of a mirror line to the symmetry content of Class 2. This mirror line is indicated by a red solid line. (3). The added mirror line generates two more motifs as indicated. The resulting motif pattern implies a second mirror plane, indicated by a blue solid line. The symmetry configuration is now that of Class 2mm, and is equivalent -- with respect to symmetry -- to the pattern of (4). (4). 2mm symmetry pattern, equivalent to that depicted in (3). |
Addition of a mirror line to the symmetry content of Class 3 yields Class 3m. See Figure 10.
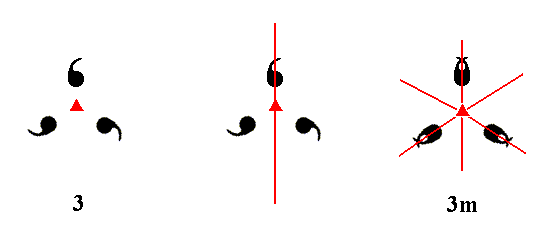
Figure 10. A mirror line added to the symmetry content of Class 3 duplicates the motifs as indicated. The resulting motif pattern implies two more mirror lines, and as such is consistent with the symmetry of Class 3m. The 3-fold rotation axis, perpendicular to the plane of the drawing, is indicated by a small red solid triangle.
Addition of a mirror line to the symmetry content of Class 4 yields Class 4mm. See Figure 11.
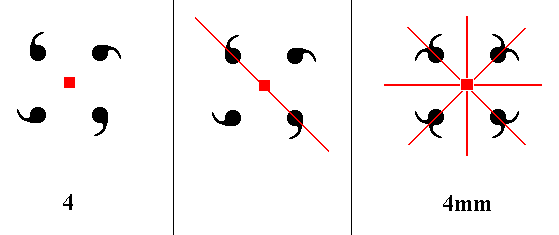
Figure 11. A mirror line added to the symmetry content of Class 4 will be duplicated by the 4-fold rotation axis resulting in a second mirror line perpendicular to the added mirror line. These two mirror lines will duplicate the motifs as indicated. The resulting motif pattern now implies two more mirror lines precisely between the added and the implied mirror lines. The symmetry configuration is now consistent with that of Class 4mm. The 4-fold-rotation axis, perpendicular to the plane of the drawing, is indicated by a small red solid square.
Addition of a mirror line to the symmetry content of Class 6 yields Class 6mm. See Figure 12.
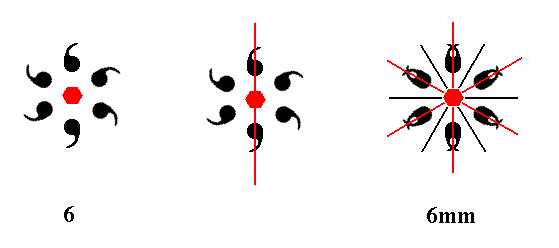
Figure 12. A mirror line added to the symmetry content of Class 6 will be multiplied by the 6-fold rotation axis resulting in three mirror lines making angles of 600 with each other. These three mirror lines will duplicate the motifs as indicated. The emerging motif pattern implies yet three more mirror lines bisecting the angles of the first three mirror lines. The resulting symmetry configuration is now consistent with that of Class 6mm. The 6-fold axis, perpendicular to the plane of the drawing, is indicated by a small red solid hexagon.
The next Figure depicts the 10 derived planar symmetry patterns, representing the ten 2-D Point Groups and at the same time the ten 2-D Crystal Classes.
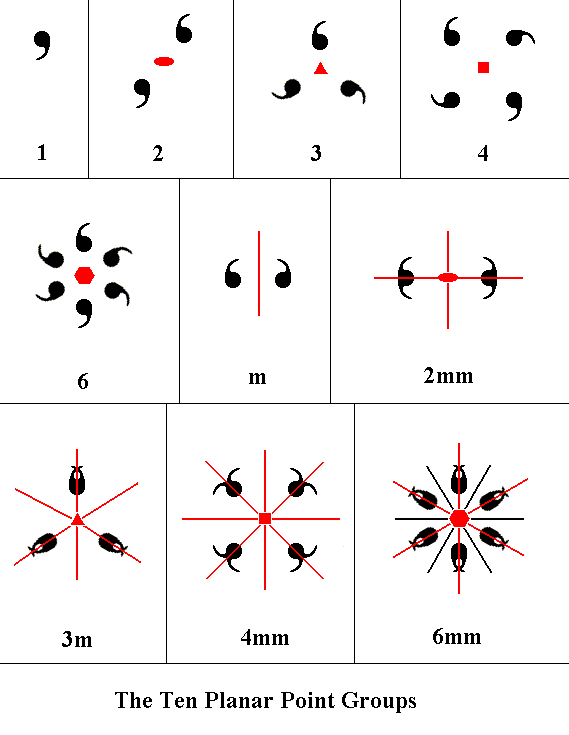
Figure 13. The ten Planar Point Groups represented by motif patterns. The symmetry content of each pattern is indicated by graphical symbols ( line, solid ellipse, solid triangle, solid square and solid hexagon ), and the Hermann-Maugin symbols for each of the ten Classes are given. In the latter symbols "mm" in 2mm, 4mm and 6mm, means that there are two different types of mirror lines present, i.e. the mirror lines present fall into two non-equivalent categories. This in contradistinction to the Class 3m, where all three mirror lines are equivalent.
The symmetry of 2-D regular arrays of repeated motifs
As has been said, we're now going to place these planar motifs in the 2-D Nets given above, i.e. we're now going to consider not just the ten planar motifs (represented by a pattern of commas), but regular periodic arrays of such motifs. In order to remain regular -- which here means periodic -- a particular 2-D lattice can only accomodate motifs having a point symmetry compatible with the point symmetry of that lattice. Let us take a closer look at the latter.
Figure 14 shows the point symmetry of each of the five two-dimensional lattices (nets). Note that a characterization in terms of point symmetry means that we only consider the symmetries around one point (For this point we have chosen a node of the net). At this point we see, for example, a 2-fold rotation axis (In 2-D patterns such an axis can only be perpendicular to the plane of the drawing). But it is clear that there are much more of such axes, going through other locations in the net. But, again, here we are considering only the point symmetry of the lattice, not its complete symmetry. In doing so we think of the lattice being extended indefinitely over the two-dimensional plane.
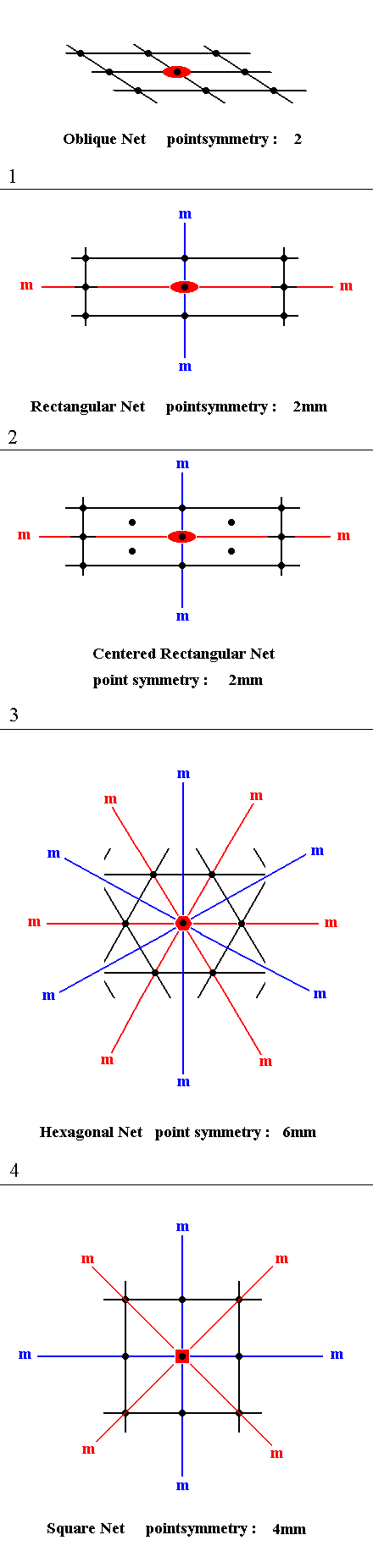 |
Figure 14.
Point symmetry of the five plane lattice types.
(1). Point symmetry of the (2). Point symmetry of the 2-D Rectangular Lattice type. (3). Point symmetry of the 2-D Centered Rectangular Lattice type. (4). Point symmetry of the 2-D Hexagonal Lattice type. (5). Point symmetry of the 2-D Square Lattice type. |
All the points (nodes) belonging to the same net are equivalent. This means that when we place motifs in such a net (2-D Lattice type) those nodes must remain equivalent. The motifs may not disturb their equivalence (If they did then the array would not be a lattice anymore). And, as has already been stated, the point symmetry of the motifs should be compatible with the point symmetry of the lattice (net). The symmetry elements of the motifs should be aligned with those of the lattice (net).
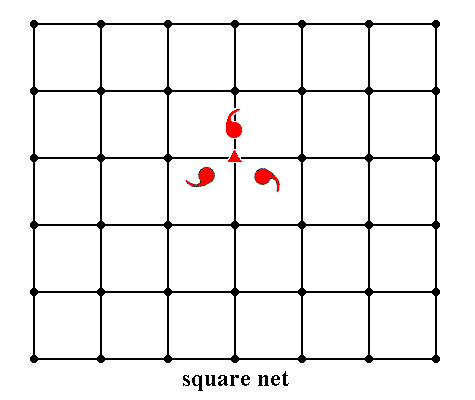
Figure 15. A motif (consisting of three motif units) with point symmetry 3 is inserted into a square lattice.
As can bee seen, the symmetry of the motif is destroyed by its insertion into the square lattice. Recall that when motifs s.str. are inserted into a lattice, to produce a regular array of them, the environment of each motif s.str. also belongs to the motif (s.l). The resulting motif s.l. has lost its 3-fold symmetry.
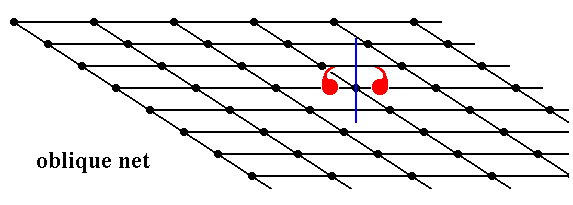
Figure 16. A motif (consisting of two motif units) with point symmetry m is inserted into an oblique lattice.
As can be seen the reflection symmetry of the motif s.str. is destroyed by its surroundings.
Motifs can, however, legitimately be inserted when they have a lower symmetry than the lattice if their symmetry elements are aligned with the corresponding symmetry elements of the lattice (net). The pattern will then express the motif's lesser degree of symmetry. This situation is a two-dimensional analogue to hemihedric or tetartohedric in three-dimensional crystals. In the next Figures we will give examples of compatibility of the motifs with the lattice in which they are placed (Also here, for reasons of clarity, only one node of the net is provided with a motif, while we should imagine that every node of the net is provided with a motif). The underlying points (nodes) only remain lattice points when they, together with their assigned motifs, are totally equivalent to each other. Only then we can speak of a periodic array of motifs, i.e. a pattern consisting of a translative repetition of motifs.
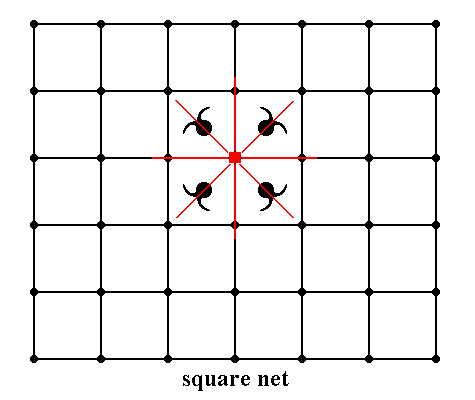
Figure 17. Insertion of a motif with point symmetry 4mm into a square lattice.
The symmetries of motif and lattice are completely compatible. The periodic
array of motifs will be formed when each lattice node is provided with that motif..
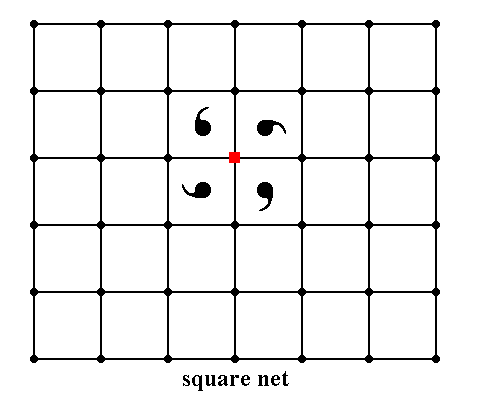
Figure 18. Insertion of a motif with point symmetry 4 into a square lattice.
Although the symmetry of the motif is lower than that of the lattice, the symmetries of motif and lattice are completely compatible (i.e. the symmetry of the motif is not destroyed by its surroundings (the lattice)). The resultant symmetry of the array of motifs -- when every node is provided with that motif -- expresses the motif's lower symmetry, by the absence of mirror lines.
If we take into account the presence of compatible motifs in the lattice, then we have a periodic array of those motifs, and then new symmetries -- other than just point symmetries -- come into play. These are :
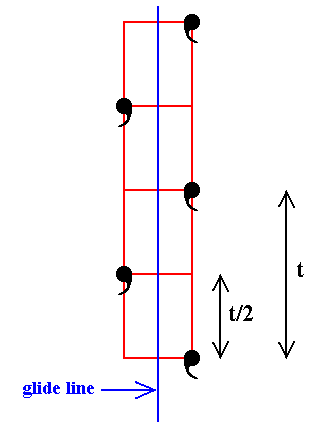 |
Figure 19. The operation of a glide line performed on a motif. The initial motif is translated by the vector t/2 parallel to the glide line, immediately followed by a reflection with respect to that glide line. The shortest translational distance between motifs in the direction of the glide line is t. |
So if -- with respect to periodic patterns -- we take into account
To continue, click HERE for Part Two.
back to homepage