

back to homepage
The symmetry of regular 2-D arrays of repeated motifs (continued)
Rectangular Net and Centered Rectangular Net.
The highest symmetrical motif that the Rectangular Net (and also the Centered Rectangular Net) can accommodate for is a motif with the same point symmetry as that of the net (lattice). The Rectangular Net as well as the Centered Rectangular Net has point symmetry 2mm. So the highest symmetrical motif, that can be placed in it, will have that same point symmetry. It then represents the highest symmetrical Class of the 2-D Rectangular Crystal System, the Class 2mm. The next Figure depicts an example of such a motif with 2mm symmetry.
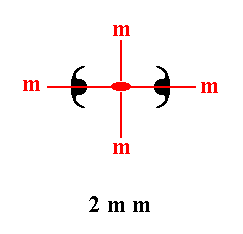
Figure 1. Two motif units (black), together forming a motif with point symmetry 2mm.
Red solid lines signify mirror lines.
The small red solid ellipse signifies a 2-fold rotation axis perpendicular to the plane of the drawing. The two mirror lines are not equivalent.
Also the motif in the next Figure has 2mm symmetry.
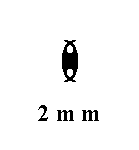
Figure 2. A motif with 2mm symmetry.
This Class (2mm) can be based on several different internal structures, which means that more than one Plane Group is possible to support it. Such a Plane Group represents the total symmetry content (point symmetry as well as translational symmetry) of the pattern of repeated motifs.
The Rectangular Net and the Centered Rectangular Net, can also accommodate for motifs having a lower symmetry than the net itself, provided their symmetry elements are aligned with the corresponding symmetry elements of the net. Only one such lower symmetry is possible, namely m. It represents the lowest symmetrical Class (planar Point Group), m, of the 2-D Rectangular Crystal System. So this System has two Classes, 2mm and m.
The Class m can be based on three possible internal structures. So it can be supported by one of three possible Plane Groups, and these are :
In what follows we will first investigate the Plane Groups associated with the Point Group 2mm.
When we insert motifs with 2mm symmetry into a primitive Rectangular Net (primitive Rectangular 2-D Lattice), we can get the following pattern (See Figure 3) :
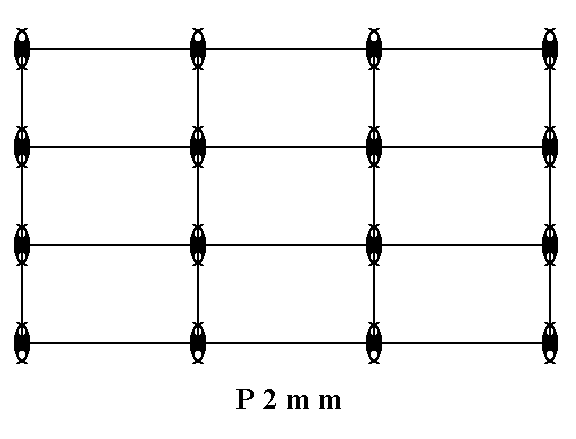
Figure 3. Placing motifs with 2mm point symmetry in a primitive rectangular 2-D lattice creates a periodic pattern of these motifs representing the Plane Group P2mm.
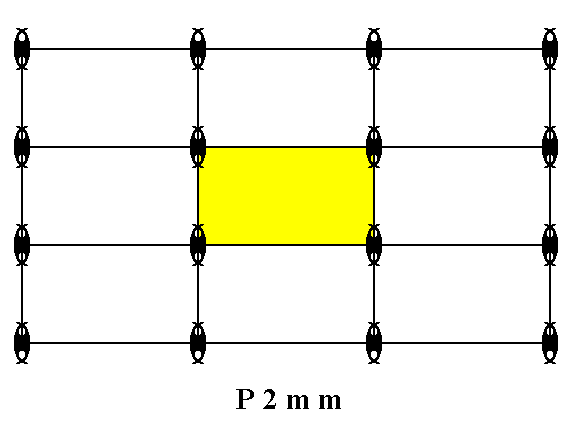
Figure 3a. A unit mesh choice is given in yellow. Its point symmetry is 2mm , and it is a primitive mesh ( P ) .
If we eliminate all translations, and thus telescope the pattern into itself, we end up with the motif depicted in the next Figure.

Figure 3b. Removing all translations from the pattern representing Plane Group P2mm (Figure 3) gives, in the present case, the motif s.str. and the motif s.l. ( The motif s.l. is the motif in the usual sense + its proper surroundings -- here given in blue).
This motif has point symmetry 2mm, and represents as such the point symmetry associated with the pattern of Figure 3, or in other words, it is the pattern's translation-free residue.
As can be seen from the pattern in Figure 3, the symmetry of the Plane Group P2mm consists of simple translations, 2-fold rotation axes and mirror lines.
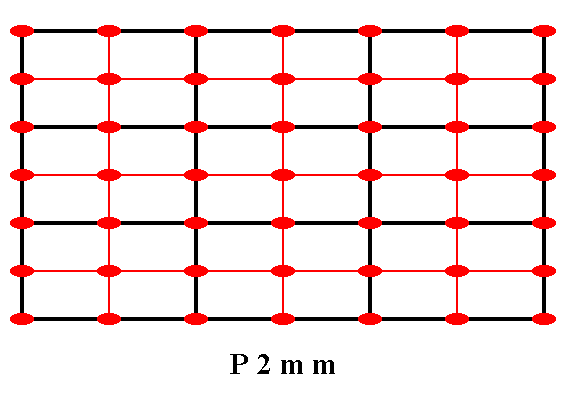
Figure 3c. The total symmetry content of the Plane Group P2mm.
Solid lines (black and red) indicate mirror lines.
Small red solid ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
So we now have the first Plane Group on which the Class 2mm can be based.
The (primitive) Rectangular Net can also accommodate for motifs having a lesser degree of point symmetry, provided that their symmetry elements are aligned with the corresponding symmetry elements of the net. Such a motif can either have a point symmetry of 2, i.e. having a 2-fold rotation axis as its only symmetry element, or have a point symmetry of m , i.e. having a mirror line as its only symmetry element. We'll start with the latter type of motif.
Two such motifs are placed in a mesh of a primitive rectangular net as follows :
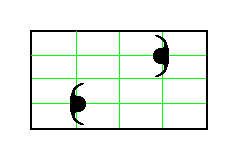
Figure 4. Two motifs, each having point symmetry m , are placed in a mesh of a primitive rectangular lattice, as indicated.
The next Figure depicts a regular periodic pattern of motifs, that have a symmetry m, resulting in the Plane Group P2mg.
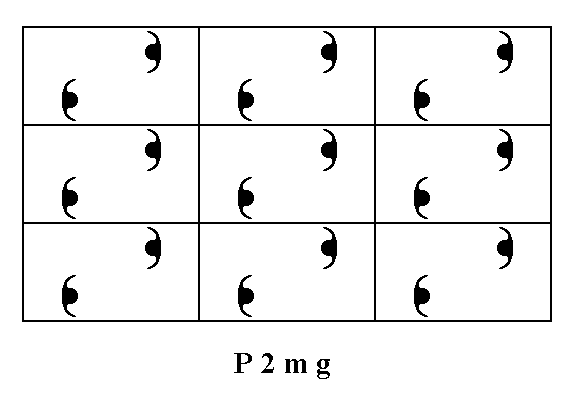
Figure 4a. If we place two motifs, having a symmertry of m , in each mesh of the primitive net, as indicated in Figure 4, then we will obtain a periodic pattern of motifs representing the Plane Group P2mg.
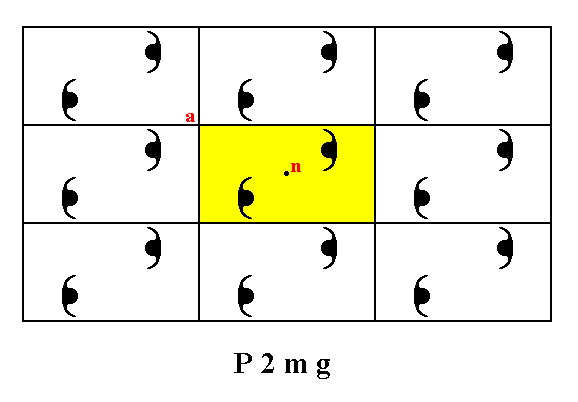
Figure 4b. For the pattern of Figure 4a a unit mesh is chosen ( yellow). This unit mesh has point symmetry 2, and is primitive (P).
Point n is not equivalent to point a, because the orientations of the motifs bottom-left and top-right to them are different. So indeed the unit mesh is primitive
The next Figure gives the motif s.str. and the motif s.l. of the pattern of Figure 4a. The motif s.l. is repeated indefinitely across the two-dimensional plane.
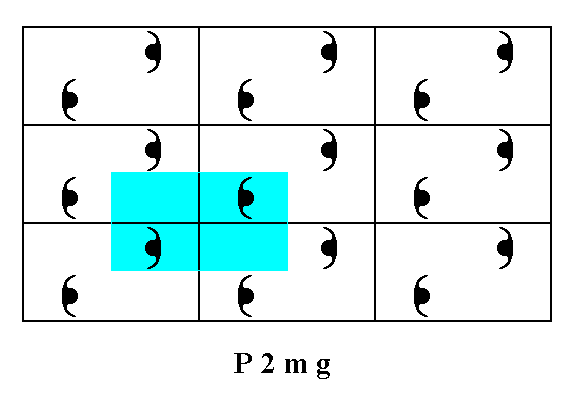
Figure 4c. The motif s.str. (black) and the motif s.l. (black + blue) of the pattern representing Plane Group P2mg. It is indefinitely repeated along the directions of the
2-D lattice.
To determine the translation-free residue (i.e. to determine the point group symmetry) of the pattern representing the Plane Group P2mg, we contract the whole structure together till all translations are zero. The figure (shape, pattern) we end up with is depicted in the next Figure.

Figure 4d. Eliminating all translations yields a figure that has a point symmetry 2mm , which represents the translation-free residue of the Plane Group P2mg.
In the pattern, representing the Plane Group P2mg we can detect 2-fold rotation axes, mirror lines and glide lines.
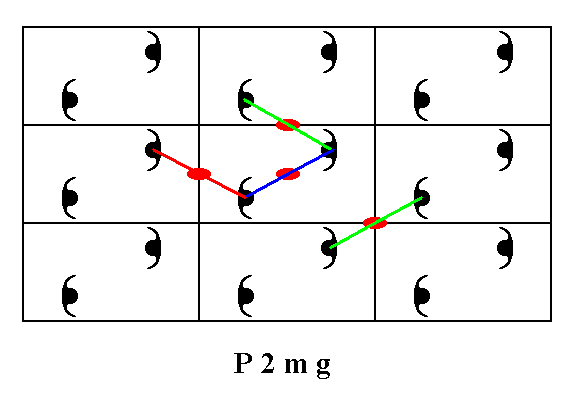
Figure 4e. Some of the 2-fold rotation axes, belonging to the symmetry content of the Plane Group P2mg, are indicated. The colored lines serve to show that there indeed are 2-fold rotation axes perpendicular to the plane of the drawing.
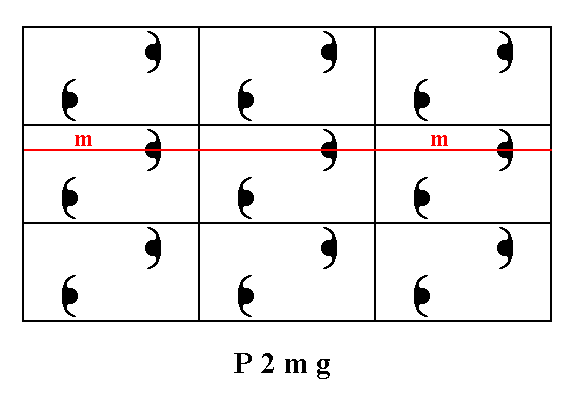
Figure 4f. The pattern representing Plane Group P2mg has mirror lines parallel to the y direction. One of them is depicted.
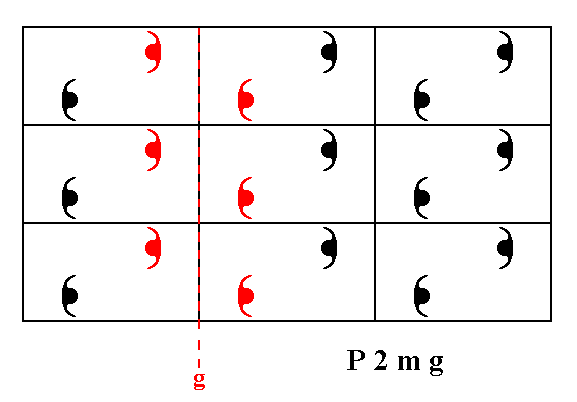
Figure 4g. The pattern representing Plane Group P2mg has glide lines parallel to the x direction. One of them is depicted.
The total symmetry content of Plane Group P2mg is given in the next Figure.
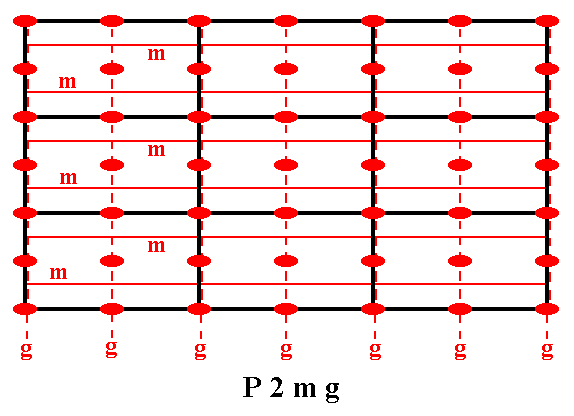
Figure 4h. Total symmetry content of the Plane Group P2mg.
Solid red lines indicate mirror lines.
Small solid red ellipses indicate 2-fold rotation axes perpendicular to the plane of the drawing.
The glide lines are all parallel to the x direction, some going through the mid-line of the rectangles, others coinciding with their sides. They are indicated by red dashed lines.
So now we have determined the second possible Plane Group on which the Class 2mm can be based.
The primitive Rectangular Net can also accommodate motifs possessing only 2-fold rotational symmetry, i.e. motifs having a point symmetry 2. Figure 5 shows a regular array of such motifs, based on a primitive rectangular net. The pattern represents the Plane Group P2gg.
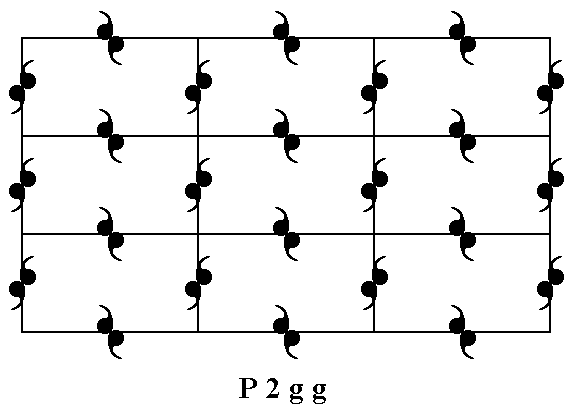
Figure 5. Motifs possessing only a 2 symmetry can be accommodated in a primitive 2-D rectangular lattice, resulting in a periodic structure.
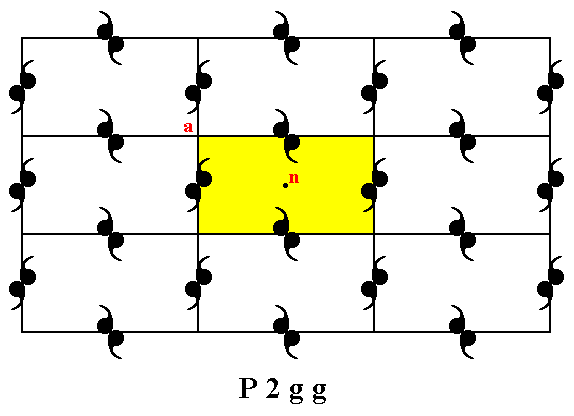
Figure 5a. A unit mesh choice (yellow). This unit mesh is primitive and has a point symmetry of 2.
Point n is not equivalent to point a, because the orientations of the motifs left and right to them are different. So indeed the unit mesh is primitive.
As can be seen in the patterns of the above Figures the "motifs" are not the units that are repeated over and over in the net. In fact they are just motif units, and indeed two such units, that are symmetric with respect to each other, are repeated.
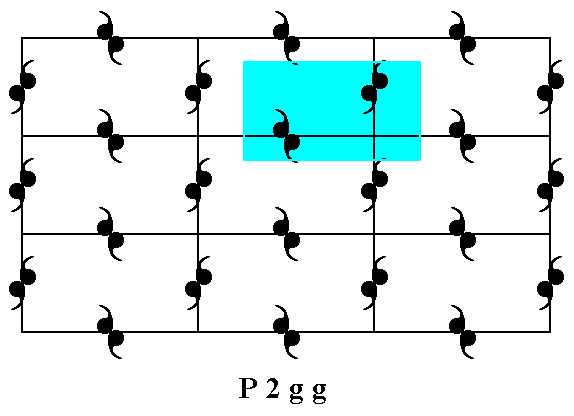
Figure 5b. The motif s.str. (black) and the motif s.l. (black + blue) in the pattern representing Plane Group P2gg.
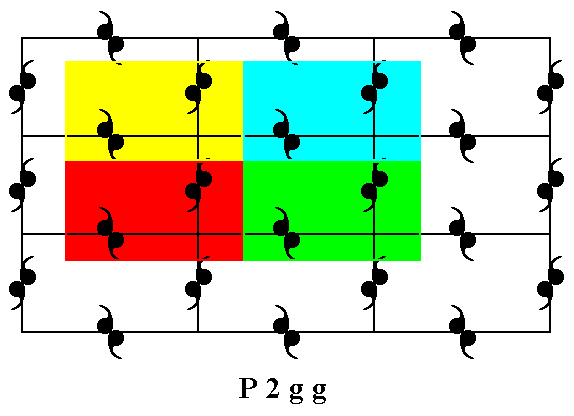
Figure 5c. The motif s.l. is indeed repeated over and over again (four repeats are indicated), and tiles the entire 2-D plane.
If all translations in the pattern representing Plane Group P2gg are eliminated (by telescoping the structure into itself), then a figure will emerge that has 2mm symmetry. This shows that the Point Group associated with the Plane Group P2gg, i.e. the translation-free residue of that Plane Group, is 2mm, representing the Crystal Class based on this Plane Group. See Figure 5d.

Figure. 5d. The translation-free residue of the Plane Group P2gg is its Point Group. As can be seen, the figure (shape), representing this translation-free residue, has 2mm symmetry.
The pattern representing Plane Group P2gg has 2-fold rotation axes at the nodes of the lattice, at the centers of the edges of the meshes, as well as in the center of each mesh. See Figure 5e.
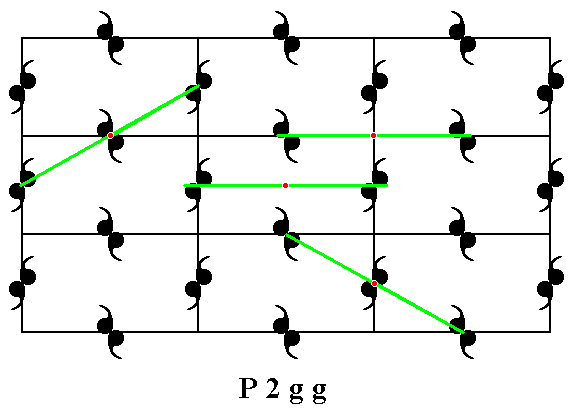
Figure 5e. The center of each mesh, as well as the centers of the edges of each mesh, and also the nodes of the net, contain a 2-fold rotation axis (indicated by a red point) perpendicular to the plane of the drawing. Some examples of these axes (clarified by means of green lines) are indicated.
The pattern representing Plane Group P2gg also has two types of glide lines, namely parallel to the x direction and parallel to the y direction. See Figures 5f and 5fa.
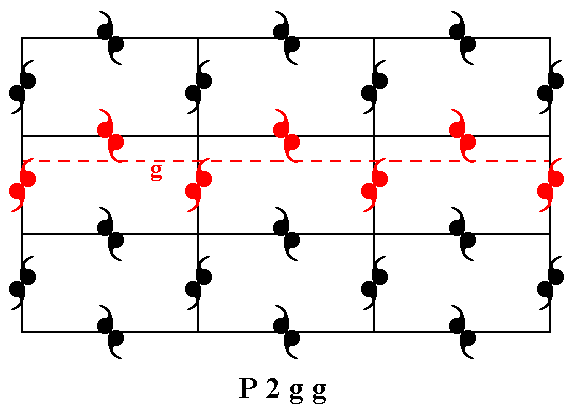
Figure 5f. The pattern representing Plane Group P2gg has glide lines parallel to the y direction. One of them is indicated.
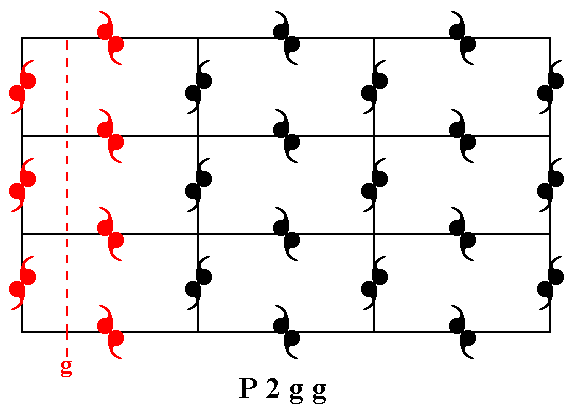
Figure 5fa. The pattern representing Plane Group P2gg has glide lines parallel to the x direction. One of them is indicated.
The total symmetry content of the Plane Group P2gg is given in the next Figure.
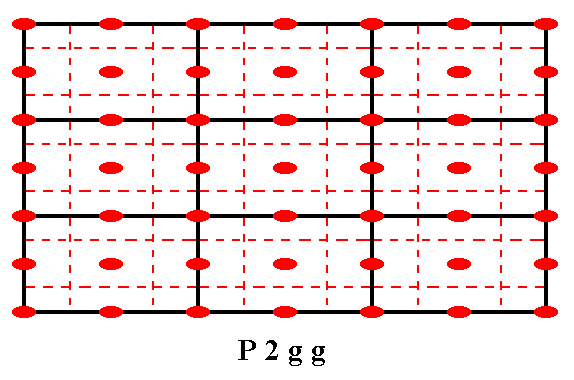
Figure 5g. The total symmetry content of the Plane Group P2gg.
2-fold rotation axes perpendicular to the plane of the drawing are indicated by small solid red ellipses.
Glide lines are indicated by dashed red lines.
Mirror lines are absent.
So now we have determined the third possible Plane Group on which the Class 2mm can be based. These are all the possibilities with respect to placing motifs in the primitive Rectangular Net.
In the centered Rectangular Net we can place motifs with 2mm symmetry to obtain yet another Plane Group associated with the Point Group 2mm. Placing the other possible motifs in the centered Rectangular Net does not yield new and different Plane Groups anymore.
In the next Part we will continue our investigation of periodic planar patterns, and place motifs with 2mm symmetry in a centered rectangular net.
To continue, click HERE for Part Four.
back to homepage