back to homepage
back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six
back to Part Seven
back to Part Eight
This Class can be derived from the Forms of the Trigonal Hemihedric Division (= Ditrigonal-dipyramidal Class) by applying hemimorphy to those Forms. This means that in the Forms of the Trigonal Hemihedric Division we suppress the equatorial mirror plane (that contains the horizontal crystallographic axes). The mirror planes that remain are the three vertical mirror planes that bisect the angles between the horizontal crystallographic axes. The result is that faces at the top of a crystal belong to different Forms of this Class than those at the underside of the crystal. The symmetry elements of this Class are :
Trigonal Bipyramid
Trigonal Hemihedric Type II Hexagonal Bipyramid
Ditrigonal Bipyramid
Trigonal Prism
Trigonal Hemihedric Type II Hexagonal Prism
Ditrigonal Prism
Trigonal Hemihedric Basic Pinacoid
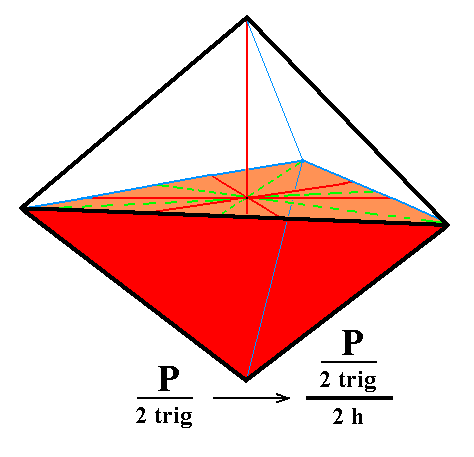
From the trigonal hemihedric trigonal bipyramid can be derived the trigonal monopyramid when we subject it to hemimorphy. The bipyramid decays in two independent halves -- monopyramids -- an upper and a lower one. See Figure 1. Both monopyramids are open Forms, which here means that such a pyramid is not closed by a basal (horizontal) face, it just consists of three faces. In figure 1a one such monopyramid is shown.
The symbol "2 h" in the Naumann expression means that hemimorphy is applied to the trigonal hemihedric trigonal bipyramid.
 |
Figure 1. Derivation of two possible Trigonal Monopyramids from the trigonal hemihedric Trigonal Bipyramid, by suppression of the equatorial mirror plane, expressed by the suppression of either the lower faces (indicated as red) or the upper faces (indicated as white). |
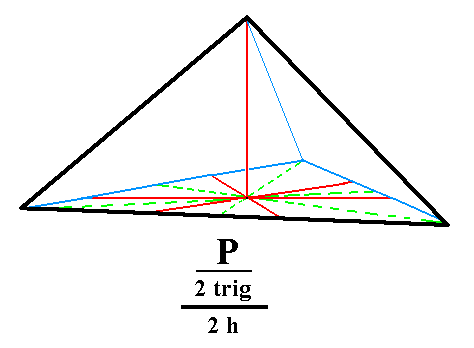 |
Figure 1a. The Trigonal Monopyramid derived from the white faces of the bipyramid of Figure 1. |
From the trigonal hemihedric type II hexagonal bipyramid can be derived two type II hexagonal monopyramids. These also are open Forms. See Figure 2 and 2a.
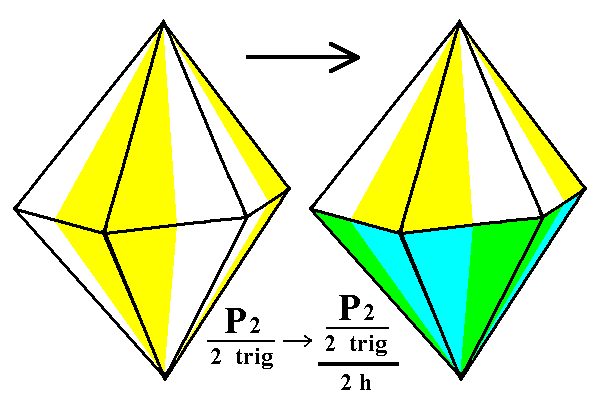
Figure 2. Derivation of the hemimorphous trigonal hemihedric Type II Hexagonal Monopyramid from the trigonal hemihedric Type II Hexagonal Bipyramid.
The colors symbolize the symmetries involved.
Two independent Monopyramids are possible depending on the suppression of either the yellow/white faces (= upper faces) or of the green/blue faces (= lower faces). The latter possibility is depicted in Figure 2a.
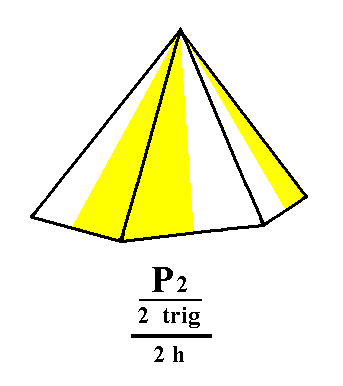 |
Figure 2a. The hemimorphous trigonal hemihedric Type II Hexagonal Monopyramid derived from the yellow/white faces of the right bipyramid of Figure 2. |
From the ditrigonal bipyramid can be derived the ditrigonal monopyramid by applying hemimorphy to it. See Figure 3.
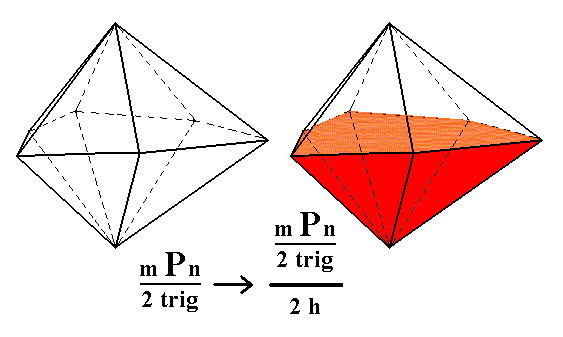
Figure 3. Derivation of hemimorphous Ditrigonal Monopyramids from a Ditrigonal Bipyramid.
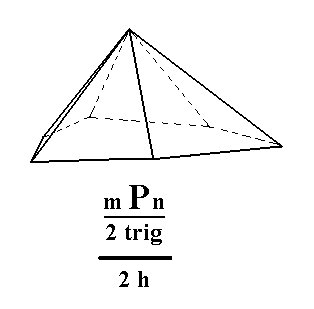 |
Figure 3a. The hemimorphous Ditrigonal Monopyramid derived from the white faces of the right bipyramid of Figure 3. |
From the trigonal prism can be derived a hemimorphous Trigonal Prism, which has the same external shape but lacks equatorial symmetry. See Figure 4.
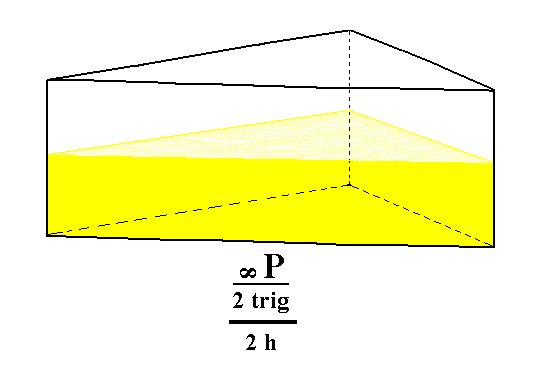
Figure 4. The hemimorphous Trigonal Prism.
From the trigonal hemihedric type II hexagonal prism can be derived a hemimorphous (trigonal hemihedric) type II hexagonal prism. It has the same shape. The suppression of the equatorial mirror plane does not lead to a loss of faces. See Figure 5.
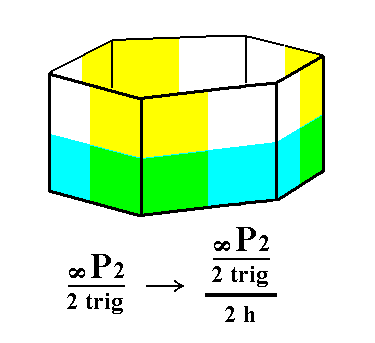 |
Figure 5. The hemimorphous (trigonal hemihedric) Type II Hexagonal Prism derived from the trigonal hemihedric type II Hexagonal Prism. |
From the ditrigonal prism we can derive the hemimorphous ditrigonal prism. Its shape remains the same, because the suppresion of the equatorial mirror plane does not cause a loss of faces. See Figure 6.
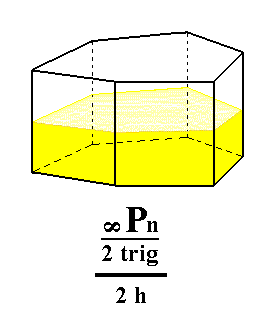 |
Figure 6. Derivation of the hemimorphous (trigonal hemihedric) Ditrigonal Prism from the trigonal hemihedric Ditrigonal Prism. |
From the trigonal hemihedric basic pinacoid we can derive the pedion. The latter is a single horizontal face : by suppressing the equatorial mirror plane of the basic pinacoid we get in fact two such faces, i.e. two independent horizontal faces, an upper one and a lower one. Such a pedion can close a monopyramid by forming its base. Two such pedions (an upper and a lower one) could close a prism. See Figure 7, 7a and 7b.
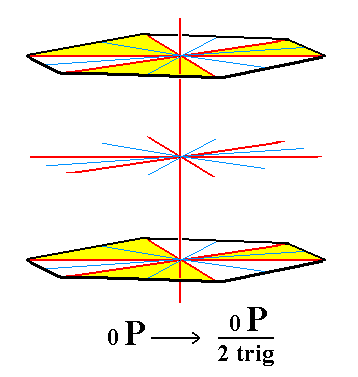 |
Figure 7. The trigonal hemihedric Basic Pinacoid (derived from the holohedric Basic Pinacoid) will be subjected to hemimorphy, resulting in two Pedions (Monohedrons) which are depicted in the next two Figures. The system of four crystallographic axes is indicated (red lines). |
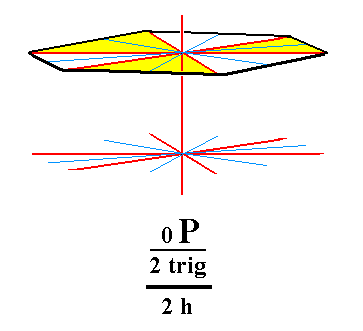 |
Figure 7a. Upper Pedion, derived from the trigonal hemihedric Basic Pinacoid, by suppression of the equatorial mirror plane, expressed by the removal of the lower face. |
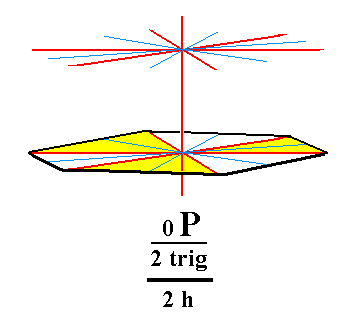 |
Figure 7b. Lower Pedion, derived from the trigonal hemihedric Basic Pinacoid, by suppression of the equatorial mirror plane, expressed by the removal of the upper face. |
This concludes our derivation of all the Forms of the Ditrigonal-pyramidal Crystal Class by means of the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Ditrigonal-pyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
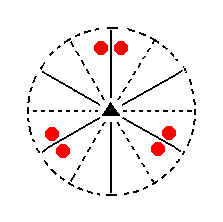 |
Figure 8. Stereogram of the symmetry elements of the Ditrigonal-pyramidal Crystal Class, and of all the faces of the most general Form. |
The face a : ~a : -a : c generates a trigonal monopyramid when subjected to the symmetry elements of the present Class : The action of the 3-fold rotation axis multiplies the face by three. Then the mirror plane symmetry is already implied (i.e. it does not add any new faces anymore). See Figure 9.
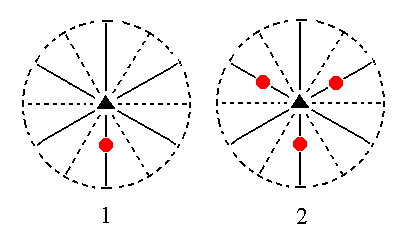 |
Figure 9. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Stereogram of the generated Trigonal Monopyramid. |
The face 2a : 2a : -a : c generates a hemimorphous (trigonal hemihedric) Type II hexagonal monopyramid when subjected to the symmetry elements of the present Class : The action of the 3-fold rotation axis multiplies this face by three. Each of these faces is then duplicated by a nearby mirror plane. See Figure 10.
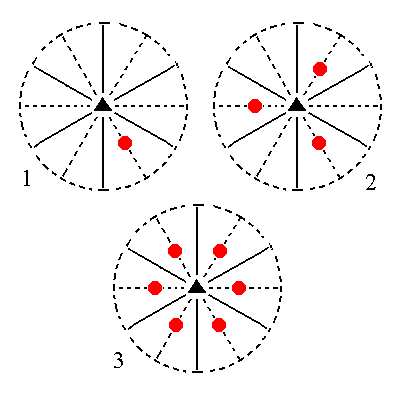 |
Figure 10. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Multiplication by three in virtue of the action of the 3-fold rotation axis. (3). Duplication of each face in virtue of the mirror planes. |
The face [3/2]a : 3a : -a : c is a definite face. Here we consider its general version, namely the face [s/(s-1)]a : sa : -a : c. It has a general position within the stereographic projection, and generates a ditrigonal monopyramid when subjected to the symmetry elements of the present Class : The nearby mirror plane duplicates this face, and the resulting face pair is multiplied by three in virtue of the 3-fold rotation axis.
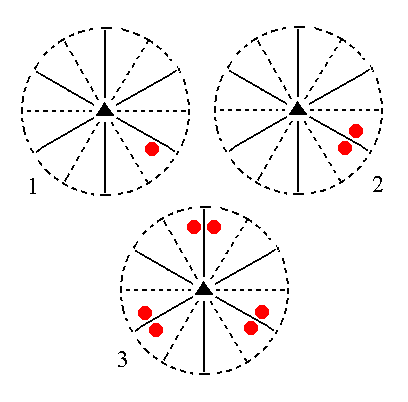 |
Figure 11. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Duplication of the face in virtue of the nearby mirror plane, resulting in a face pair. (3). Multiplication of this face pair by three in virtue of the action of the 3-fold rotation axis, resulting in a Ditrigonal Monopyramid. |
The face [3/2]a : 3a : -a : ~c is a definite one. Here we consider its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. Its orientation is vertical. It will generate a ditrigonal prism when subjected to the symmetry elements of the present Class : The nearby mirror plane will duplicate this face, resulting in a face pair. Then the 3-fold rotation axis will multiply this face pair by three resulting in six vertical faces, the ditrigonal prism. See Figure 12.
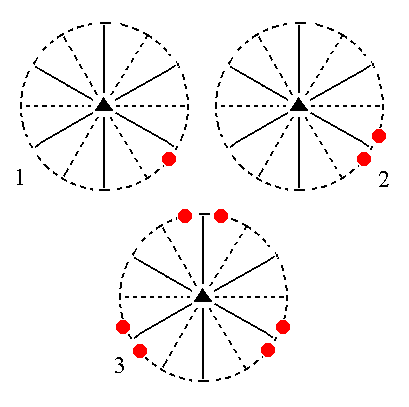 |
Figure 12. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Duplication of the face in virtue of the nearby mirror plane, resulting in a vertical face pair. (3). Multiplication of this face pair by three in virtue of the action of the 3-fold rotation axis, resulting in a Ditrigonal Prism. |
The face a : ~a : -a : ~c is also vertical. It generates a trigonal prism when subjected to the symmetry elements of the present Class : The 3-fold rotation axis triples the face, and then the other symmetries of the Class (the mirror planes) are already implied. The result is three vertical faces, the trigonal prism. See Figure 13.
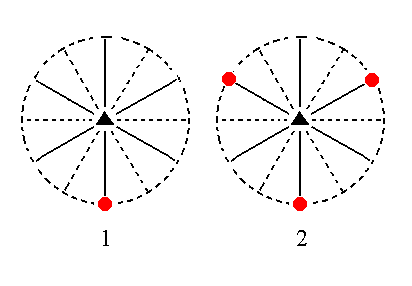 |
Figure 13. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Multiplication of this face by three in virtue of the action of the 3-fold rotation axis, resulting in a Trigonal Prism. |
The face 2a : 2a : -a : ~c is also vertical. It generates a hemimorphic trigonal hemihedric type II hexagonal prism when subjected to the symmetry elements of the present Class : The mirror plane to the left of it duplicates this face, and the resulting vertical face pair is multiplied three times in virtue of the 3-fold rotation axis. So now we have 6 vertical faces making up the hexagonal prism. See Figure 14.
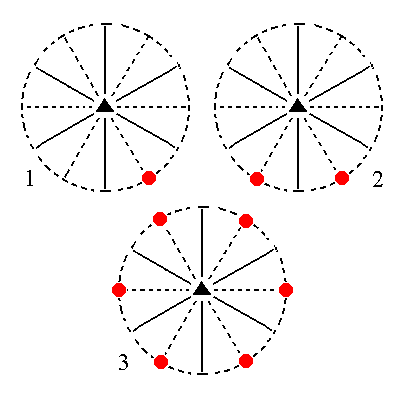 |
Figure 14. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. (2). Duplication of this face by the action of a mirror plane. (3). Multiplication of the resulting face pair by three in virtue of the action of the 3-fold rotation axis, resulting in a Hexagonal Prism. |
The face ~a : ~a : ~a : c is horizontal. Neither the 3-fold rotation axis, nor the mirror planes have any effect on it (i.e. they do not generate new faces), so this Form consists just of the one face we started with and is caled a pedion. See Figure 15.
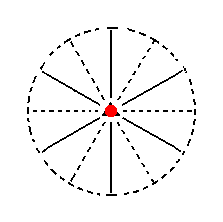 |
Figure 15. Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Ditrigonal-pyramidal Crystal Class. When we subject it to the symmetry elements of the present Class no new faces are generated, so we end up with a Pedion. |
This concludes our exposition of the Ditrigonal-pyramidal Crystal Class.
To continue, click HERE for Part Ten (Class 6* ).