The Hexagonal Crystal System (Part Ten)
back to homepage

back to Part One
back to Part Two
back to Part Three
back to Part Four
back to Part Five
back to Part Six
back to Part Seven
back to Part Eight
back to Part Nine

The Trigonal-bipyramidal Class
(= Trigonal Tetartohedric Division)   6*

This Class can be derived from the Forms of the Trigonal Hemihedric Division (= Ditrigonal-dipyramidal Class) by applying pyramidal hemihedric to those Forms. So these Forms are derived from the holohedric Forms by first applying trigonal hemihedric (Described in Part Eight) and then, to the result, pyramidal hemihedric (Described in Part Three. Such a two-fold application of hemihedrics is called a tetartohedric. The present derivation means that in the Forms of the Trigonal Hemihedric Division we suppress the rest of the vertical mirror planes. The only mirror plane that remains is the equatorial mirror plane. The symmetry elements of this Class are : In the Hermann-Maugin symbol for the symmetry of this Class the 3-fold rotation axis is given as a 6-fold roto-inversion axis (6*). This roto-inversion axis is however equivalent to a 3-fold rotation axis with a mirror plane perpendicular to it. This means that 6* = 3/m.

Derivation of the Forms of the Trigonal-bipyramidal Class
(= Trigonal Tetartohedric)

MEROHEDRIC APPROACH.
The Forms of this Class will be found when we subject the Forms of the Trigonal Hemihedric Division to pyramidal hemihedric, which means that we suppress all their left-over vertical mirror planes.
Recall that the Forms of the Trigonal Hemihedric Division were the following :

Trigonal Bipyramid
Trigonal Hemihedric Type II Hexagonal Bipyramid
Ditrigonal Bipyramid
Trigonal Prism
Trigonal Hemihedric Type II Hexagonal Prism
Ditrigonal Prism
Trigonal Hemihedric Basic Pinacoid

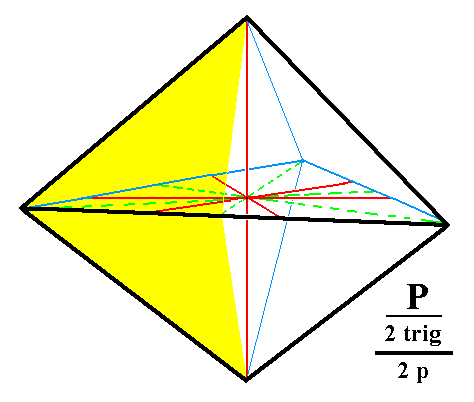
From the trigonal hemihedric trigonal bipyramid can be derived a trigonal tetartohedric type I trigonal bipyramid when pyramidal hemihedric is applied to it. No change in external shape is involved as is illustrated for two faces of the trigonal bipyramid in Figure 1 :   The suppression of the mirror plane does not effect a loss of faces.

Figure 1. The (trigonal hemihedric) Trigonal Bipyramid does not change its external shape when subjected to pyramidal hemihedric, as is shown for two of it's faces. These faces will remain present (i.e. the removal of either the white areas or the yellow areas does not lead to a loss of faces, because the orientation of the remaining parts is the same as that of the removed parts). Precisely the same holds for the other faces of the bipyramid.
The subsymbol "2 trig" and the subsymbol "2 p" in the Naumann symbol stands for trigonal hemihedric and pyramidal hemihedric respectively.
When we, as we in fact did here, apply, to the holohedric Forms, first trigonal hemihedric (= suppression of the vertical mirror planes that go through the horizontal crystallographic axes), and then subject the result to pyramidal hemihedric (= suppression of all vertical mirror planes) -- in other words, if we apply, to the holohedric Forms, trigonal tetartohedric -- we effectively suppress all vertical mirror planes. But this seems to be exactly the same as just applying pyramidal hemihedric. Nevertheless the respective results are not identical :
Applying pyramidal hemihedric to the holohedric protopyramid yields a pyramidal hemihedric hexagonal bipyramid (See Figure 1 in Part Three).
On the other hand, applying trigonal hemihedric to the holohedric protopyramid yields a trigonal bipyramid (See Figure 1a, 1b and 1c in Part Eight), and when we then apply pyramidal hemihedric to the latter it remains a trigonal bipyramid (but with lower symmetry than the trigonal hemihedric trigonal bipyramid).
So in the first case we get a hexagonal bipyramid, while in the second case we get a trigonal bipyramid, proving that trigonal tetartohedric (= first trigonal hemihedric and then pyramidal hemihedric) is not equivalent to (just) pyramidal hemihedric, although in both cases all six vertical mirror planes are suppressed and the equatorial mirror plane retained.
From the trigonal hemihedric type II hexagonal bipyramid we can derive the trigonal tetartohedric type II trigonal bipyramid when we apply pyramidal hemihedric to it. See Figures 2, 2a, 2b and 2c.

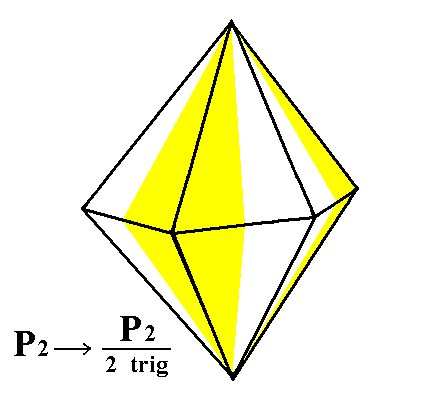  Figure 2. The trigonal hemihedric Type II Hexagonal Bipyramid, derived from the holohedric Deuteropyramid. From this trigonal hemihedric Bipyramid will be derived the Tetartohedric Bipyramid.
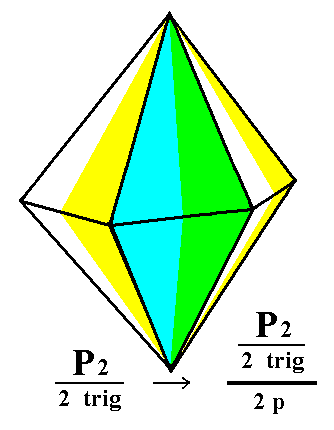  Figure 2a. Derivation of the trigonal tetartohedric Type II Trigonal Bipyramid by means of appying pyramidal hemihedric to the trigonal hemihedric Type II Hexagonal Bipyramid.
The pyramidal hemihedric is expressed by establishing two color categories of faces, namely (1) yellow/white faces, and (2) green/blue faces. By suppressing either category-1 faces or category-2 faces we obtain two possible Trigonal Bipyramids.

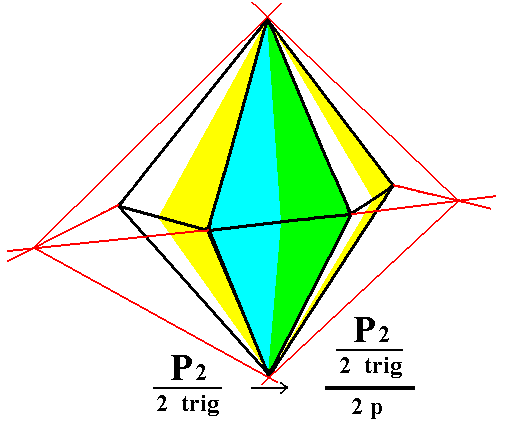
Figure 2b. Construction of a trigonal tetartohedric Type II Trigonal Bipyramid by means of suppressing the category-1 faces (yellow/white faces) and allowing the category-2 faces (green/blue faces) to extend till they meet.
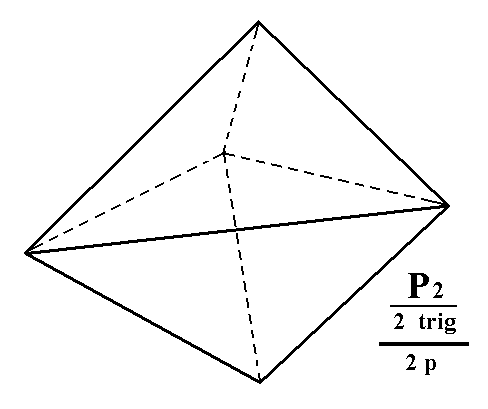  Figure 2c. The trigonal tetartohedric Type II Trigonal Bipyramid as a result of the construction in Figure 2b.
From the ditrigonal bipyramid the trigonal tetartohedric type III trigonal bipyramid can be derived when we apply pyramidal hemihedric to it (which is equivalent to applying trigonal tetartohedric to the holohedric dihexagonal bipyramid). As can be seen in the next Figure, half the faces are suppressed, so the ditrigonal bipyramid becomes a trigonal bipyramid.
See Figure 3, 3a, 3b and 3c.

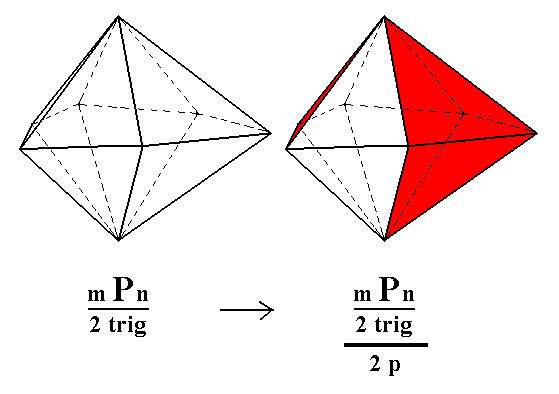
Figure 3. (1) Trigonal hemihedric Ditrigonal Bipyramid. (2). Derivation of two possible trigonal tetartohedric Type III Trigonal Bipyramids, showed by the coloring of its faces (for reasons of clarity only the directly visible faces are considered (and correspondingly colored).

To illustrate the above derivation still further, let's look at what happens to the equatorial plane -- Figure 3a -- of the ditrigonal bipyramid when it is subjected to pyramidal hemihedric resulting in a triangle, the equatorial plane of the trigonal bipyramid (in the present case it is a type III trigonal bipyramid).

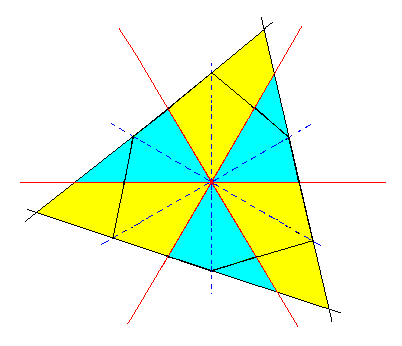  Figure 3a. Derivation of the equatorial plane of the trigonal tetartohedric Type III Trigonal Bipyramid. This plane has the shape of an equilateral triangle.
The above picture of the equatorial plane we already know, in the form of horizontal sections, from Part Seven, in which the rhombohedric tetartohedric Division (Class) is being considered. Although we find horizontal sections with the same symmetry in both Classes, those Classes differ with respect to the equatorial mirror plane, being absent in the rhombohedric tetartohedric Class (Division), the symmetry of which is 3*, and present in the Class under consideration, the symmetry of which is 6*, which is equivalent to 3/m.

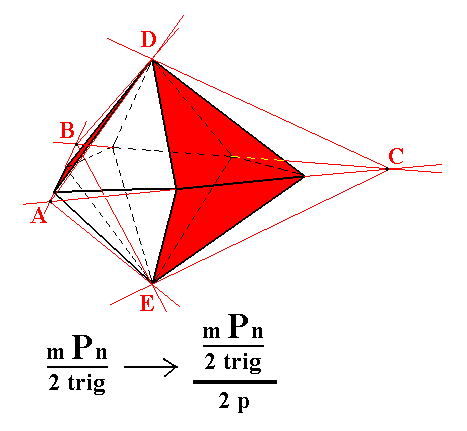
Figure 3b. Construction of a Trigonal Bipyramid ABCDE from a Ditrigonal Bipyramid, by alternately suppressing faces and allowing to extend the others.

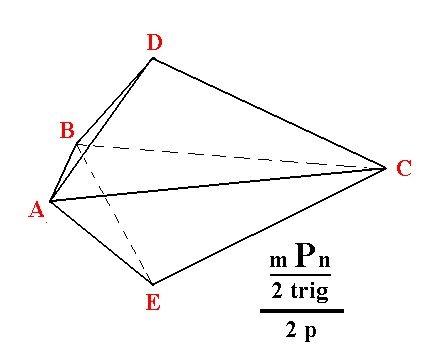  Figure 3c. Result of the construction -- in Figure 3b -- of a Trigonal Tetartohedric Type III Trigonal Bipyramid.
From the trigonal prism we can derive the trigonal tetartohedric type I trigonal prism when we subject it to pyramidal hemihedric. As can be seen in the next Figure, the external shape does not change, but of course the symmetry is lowered.

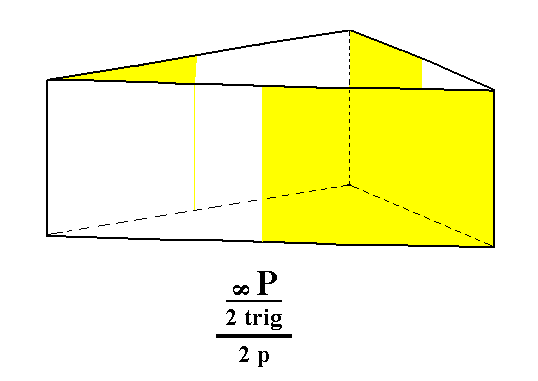
Figure 4. The trigonal hemihedric Trigonal Prism does not change its shape when subjected to pyramidal hemihedric. So the resulting trigonal tetartohedric Form is (still) a Trigonal Prism.
From the trigonal hemihedric type II hexagonal prism we can derive the trigonal tetartohedric type II trigonal prism. As can be seen in the next Figure, there is a halving of the number of faces involved, which here implies a transformation of a hexagonal prism into a trigonal prism.

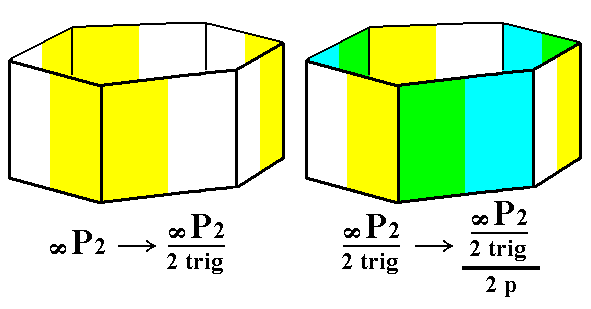
Figure 5. Derivation of the trigonal tetartohedric Type II Trigonal Prism from the trigonal hemihedric Type II Hexagonal Prism. Two such prisms can be derived depending on which category of faces -- the yellow/white or the green/blue faces -- will be suppressed (and the others allowed to extend till they meet). For one such trigonal prism, see Figure 5a and 5b.

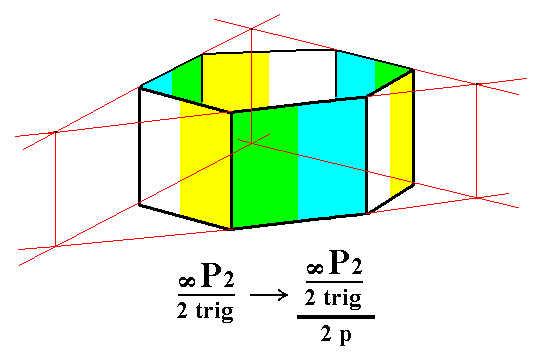
Figure 5a. Construction of a trigonal tetartohedric Type II Trigonal Prism from the green/blue faces of the prism of the right image of Figure 5.

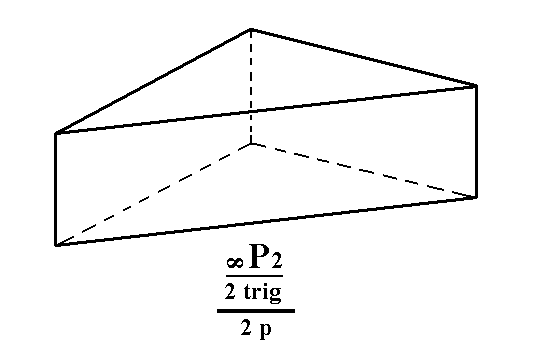
Figure 5b. Result of the construction -- in Figure 5a -- of a trigonal tetartohedric Type II Trigonal Prism.
From the ditrigonal prism we can derive a trigonal tetartohedric type III trigonal prism when we apply pyramidal hemihedric to it. In Figure 6 we can see that the result is a halving of the number of faces, so from a ditrigonal prism a trigonal prism is generated.

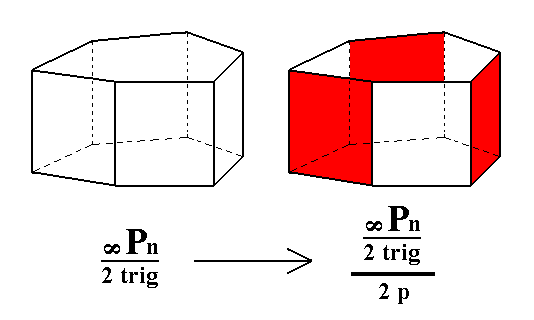
Figure 6. Derivation of the trigonal tetartohedric Type III Trigonal Prism from the trigonal hemihedric Ditrigonal Prism. Two such prisms can be derived depending on which faces are suppressed -- the ones marked red, or the ones marked white -- (and the others allowed to extend till they meet).

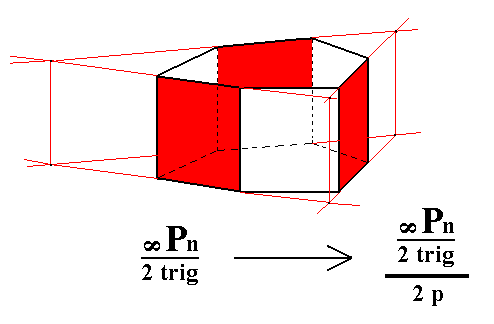
Figure 6a. Construction of a trigonal tetartohedric Type III Trigonal Prism from the red faces of the Ditrigonal Prism in the right image of Figure 6.
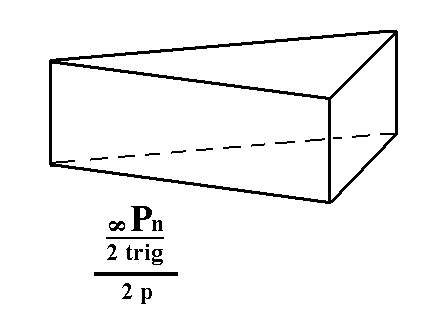  Figure 6b. Result of the construction -- in Figure 6a -- of a trigonal tetartohedric Type III Trigonal Prism.
From the trigonal hemihedric basic pinacoid we can derive the trigonal tetartohedric basic pinacoid. Removal of the remaining vertical mirror planes (= executing pyramidal hemihedric) does not have any effect concerning the shape. So the new Form is still one consisting of two horizontal parallel faces, and thus a basic pinacoid, but its symmetry is lowered accordingly. See Figures 7 and 7a.

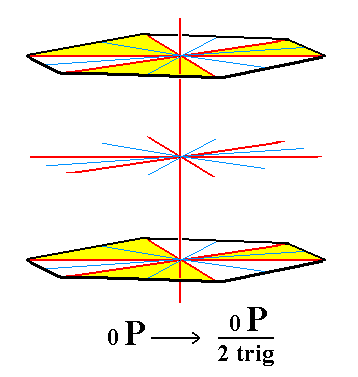  Figure 7. The trigonal hemihedric Basic Pinacoid, from which the trigonal tetartohedric Basic Pinacoid will be derived (Figure 7a).
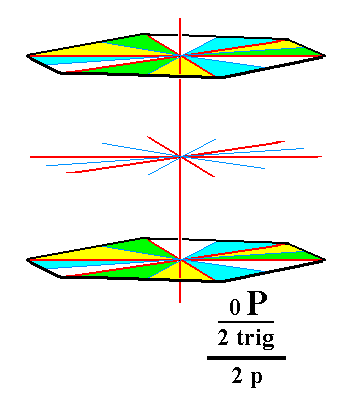  Figure 7a. The trigonal tetartohedric Basic Pinacoid.
This concludes our derivation of all the Forms of the Trigonal-bipyramidal Crystal Class, by means of the merohedric approach.
All these Forms can enter in combinations with each other in real crystals.
FACIAL APPROACH

We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Trigonal-bipyramidal Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :

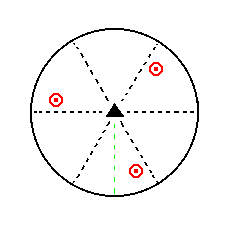The stereographic projection of the symmetry elements of this Class is given in Figure 8.

  Figure 8. Stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class, and of all the faces of the most general Form.
The face a : ~a : -a : c generates a type I trigonal bipyramid when subjected to the symmetry elements of the present Class :   The face is tripled in virtue of the 3-fold rotation axis. The three resulting faces are then reflected in the horizontal mirror plane, giving the trigonal bipyramid. See Figure 9.

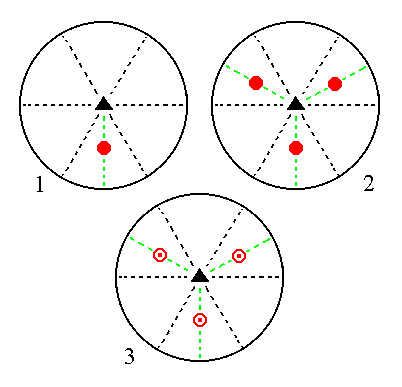  Figure 9.
(1). Position of the face a : ~a : -a : c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis.
(3). Reflection of each face in the horizontal mirror plane, resulting in three upper and three lower faces making up a trigonal bipyramid.
The face 2a : 2a : -a : c generates a type II trigonal bipyramid when subjected to the symmetry elements of the present Class :   The face is tripled in virtue of the 3-fold rotation axis. The three resulting faces are then reflected in the horizontal mirror plane yielding three upper faces and three lower faces making uo a trigonal bipyramid. See Figure 10.

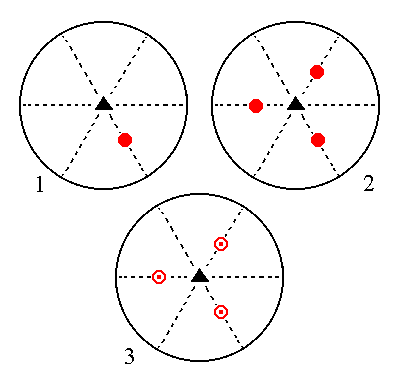  Figure 10.
(1). Position of the face 2a : 2a : -a : c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis.
(3). Reflection of each face in the horizontal mirror plane, resulting in three upper and three lower faces making up a trigonal bipyramid.
The face [3/2]a : 3a : -a : c is a definite face. Here we will consider a generalized version of it, namely the face [s/(s-1)]a : sa : -a : c. Its position in the stereographic projection is general. It will give a type III trigonal bipyramid when subjected to the symmetry elements of the present Class :   The face is tripled by the action of the 3-fold rotation axis. The three resulting faces are then reflected in the horizontal mirror plane, giving three upper and three lower faces making up a type III trigonal bipyramid. See Figure 11.

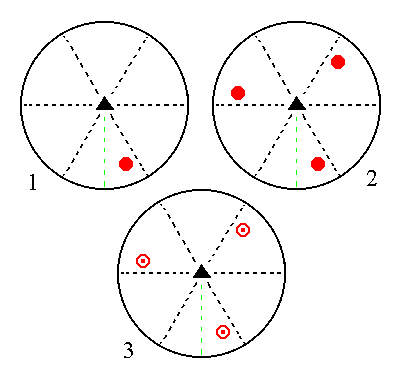  Figure 11.
(1). Position of the face [s/(s-1)]a : sa : -a : c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis.
(3). Reflection of each face in the horizontal mirror plane, resulting in three upper and three lower faces making up a trigonal bipyramid.
The face [3/2]a : 3a : -a : ~c is also a definite face. Here we will consider its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. It is a vertical face, and it generates a type III trigonal prism when subjected to the symmetry elements of the present Class : &nbp; The face will be tripled by the 3-fold rotation axis, yielding three vertical faces making up a trigonal prism. The action of the horizontal mirror plane will not give rise to any new faces because it is perpendicular to those faces. See Figure 12.

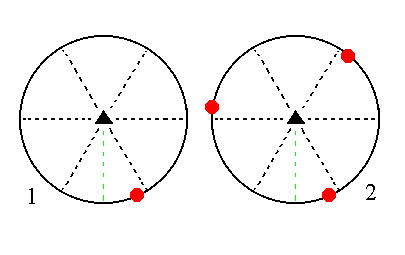  Figure 12.
(1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis, resulting in a trigonal prism.
The face a : ~a : -a : ~c is also vertical. It generates a type I trigonal prism when subjected to the symmetry elements of the present Class :   The face will be tripled by the action of the 3-fold rotation axis, resulting in three vertical faces, making up a trigonal prism. The action of the horizontal mirror plane will not generate any new faces. See Figure 13.

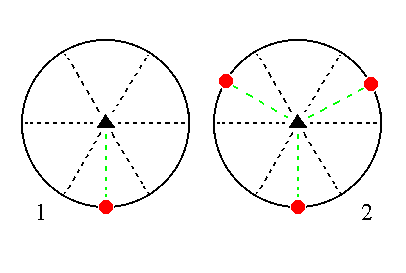  Figure 13.
(1). Position of the face a : ~a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis, resulting in a trigonal prism.
The face 2a : 2a : -a : ~c is also vertical. It generates a type II trigonal prism when subjected to the symmetry elements of the present Class :   The face is tripled by the action of the 3-fold rotation axis, resulting in a trigonal prism. The action of the horizontal mirror plane does not generate any new faces.
See Figure 14.

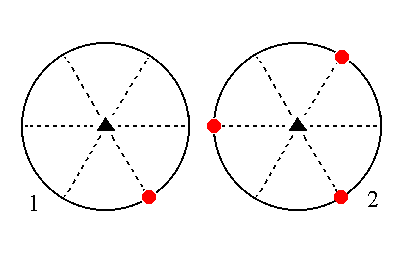  Figure 14.
(1). Position of the face 2a : 2a : -a : ~c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Tripling of the face by the action of the 3-fold rotation axis, resulting in a trigonal prism.
The face ~a : ~a : ~a : c, finally, is a horizontal face. It generates a basic pinacoid, i.e. a Form consisting of two horizontal parallel faces, when subjected to the symmetry elements of the present Class :   The action of the 3-fold rotation axis does not generate new faces, but the action of the horizontal mirror plane does. The result is two horizontal parallel faces, the basic pinacoid. See Figure 15.

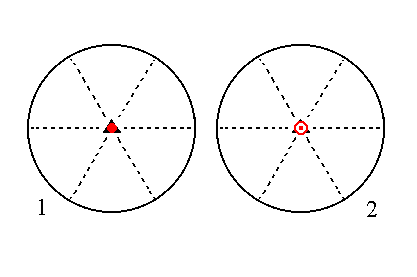  Figure 15.
(1). Position of the face ~a : ~a : ~a : c in the stereogram of the symmetry elements of the Trigonal-bipyramidal Crystal Class.
(2). Duplication of the face in virtue of the horizontal mirror plane, resulting in a Basic Pinacoid.
This concludes our exposition of the Trigonal-bipyramidal Crystal Class.
To continue, klick HERE for Part Eleven (Class 3 ).

back to homepage

back to Part One

back to Part Two

back to Part Three

back to Part Four

back to Part Five

back to Part Six

back to Part Seven

back to Part Eight

back to Part Nine

****************