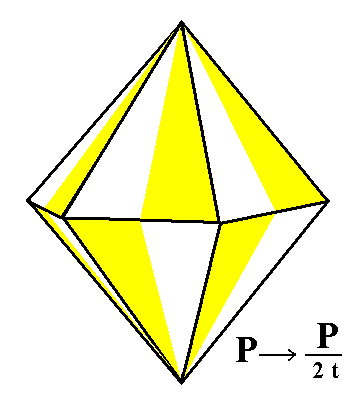
The "t" in the expression "2t" of the Naumann symbol means that a trapezohedric hemihedric is being applied.
Protopyramid (= hexagonal type I bipyramid)
Deuteropyramid (= hexagonal type II bipyramid)
Dihexagonal Bipyramid
Protoprism (= hexagonal type I prism)
Deuteroprism (= hexagonal type II prism)
Dihexagonal Prism
Basic Pinacoid
In this Class there are no mirror planes. But although in the Hexagonal-pyramidal Class (= hemimorphy of pyramidal hemihedric) also all mirror planes are absent, the resulting symmetry is different. This is because the derivation of the Forms of the present Class (from the holohedric Forms) goes by means of simultaneously dropping all mirror planes, while in the case of the derivation of the Forms of the Hexagonal-pyramidal Class this occurs in two steps : First all the vertical mirror planes are dropped, and then the resulting Form is subjected to the suppression of its horizontal mirror plane.
The holohedric hexagonal protopyramid does not change its external shape when subjected to the trapezohedric hemihedric, i.e. when all its mirror planes are suppressed simultaneously. So the result is a trapezohedric hemihedric type I hexagonal bipyramid. See Figure 1.
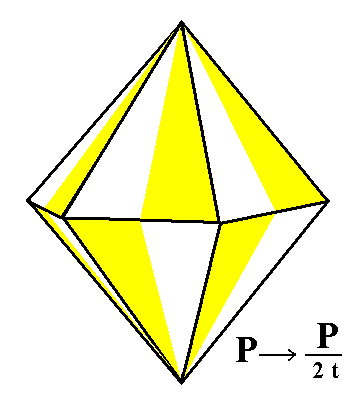 |
Figure 1. The holohedric Protopyramid looses all its mirror planes simultaneously. But, as can be seen in this Figure, this will not lead to the suppression of any face, so the external shape of the generated Form is the same as that of the corresponding holohedric Form, but the symmetry is lowered. The "t" in the expression "2t" of the Naumann symbol means that a trapezohedric hemihedric is being applied. |
The holohedric hexagonal deuteropyramid also does not change its external shape when subjected to this type of hemihedric. The resulting Form is a trapezohedric hemihedric type II hexagonal bipyramid. See Figure 2.
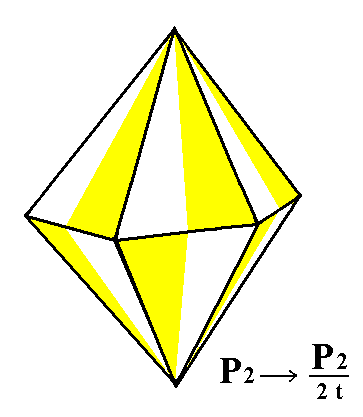 |
Figure 2. The holohedric Deuteropyramid looses all its mirror planes simultaneously. But, as can be seen in this Figure, this will not lead to the suppression of any face, so the external shape of the generated Form is the same as that of the corresponding holohedric Form, but the symmetry is lowered. The "t" in the expression "2t" of the Naumann symbol means that a trapezohedric hemihedric is being applied. |
The holohedric dihexagonal bipyramid does change its shape when it is subjected to the trapezohedric hemihedric. A hexagonal trapezohedron is formed, as can be seen in the next Figure.
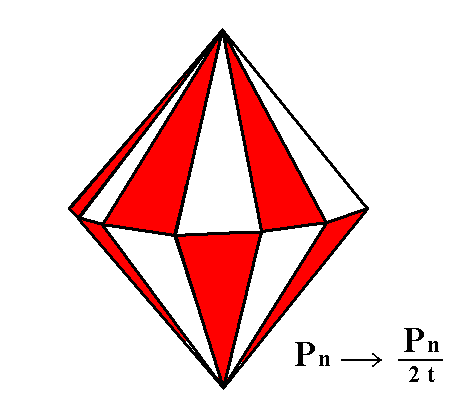
Figure 3. Suppression of all the mirror planes of the holohedric Dihexagonal Bipyramid effects suppression of alternate faces. When either the red or the white faces are suppressed and the other faces allowed to extend, two kinds of Hexagonal Trapezohedrons are formed. One of them is depicted in Figure 4.
The "t" in the expression "2t" of the Naumann symbol means that a trapezohedric hemihedric is being applied.
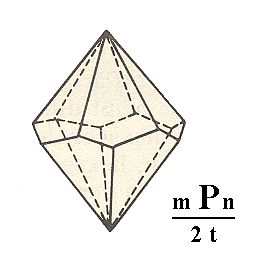 |
Figure 4. A Hexagonal Trapezohedron. The "m" in the Naumann symbol refers to the steepness of the faces. If m = 1 the c-intercept will have unit length. The "n" in the Naumann symbol refers to the general orientation of the faces with respect to the three horizontal crystallographic axes. The "t" in the expression "2t" of the Naumann symbol means that a trapezohedric hemihedric is being applied. |
Let's elaborate a little more on the generation of the hexagonal trapezohedron from the holohedric dihexagonal bipyramid in terms of horizontal sections, i.e. sections parallel to the plane containing the three horizontal crystallographic axes a1, a2 and a3. Every horizontal section through the dihexagonal bipyramid (except when going through one or the other of their tips) is a dihexagon, i.e. a plane twelve-sided figure of which all the sides are of equal length, and their angles alternately the same (that's why it is not a completely regular 12-sided figure). In the next figure we depict such a dihexagon and see what happens when all mirror planes (here in fact mirror lines) perpendicular to (the plane of) this dihexagon are removed. The result will be a regular hexagon.
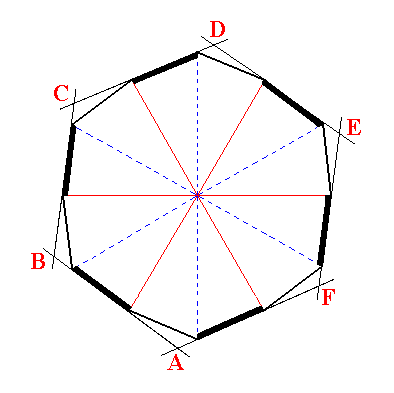 |
Figure 5. Generation of a regular hexagon (ABCDEF) from a dihexagon by dropping all mirror lines that divide the figure in symmetrical halves. |
If we consider the construction in Figure 5 as taking place somewhere above the plane of the horizontal crystallographic axes (as it is in the hexagonal trapezohedron), then we can imagine that the same construction should be expected with a corresponding section below that plane. But, because also the equatorial mirror plane is suppressed, the second construction should not be a mirror image of the first. Therefore the second construction should involve the alternates of the sides that were involved in the first construction. Only then those two constructions are not reflections of each other in the equatorial plane anymore. See Figure 6.
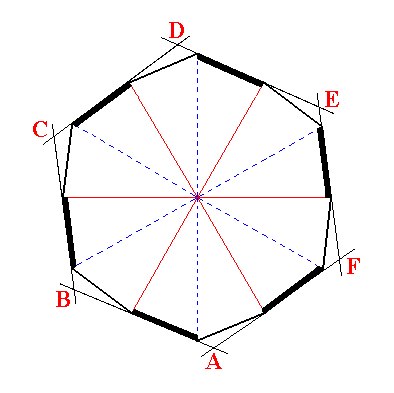 |
Figure 6. Generation of a regular hexagon (ABCDEF) from a dihexagon by dropping all mirror lines that divide the figure in symmetrical halves. |
So in the hexagonal trapezohedron we can expect two kinds of horizontal hexagonal sections. The sides of these hexagonal sections correspond to faces of the trapezohedron, and if we let those faces extend then their mutual intersections determine their shapes.
In the next Figure we will depict a superposition of the constructions of the two types of hexagons (which differ only in their being 300 rotated with respect to each other), hexagons that both simultaneaously figure in one and the same trapezohedron.
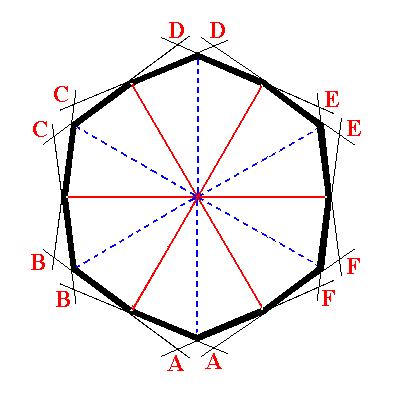 |
Figure 7. Superposition of the two constructions of regular hexagons. |
So we have two hexagons only differing in orientation by a 300 rotation. One such a hexagon represents a horizontal section through the trapezohedron somewhere above the plane which contains the horizontal crystallographic axes, the other represents such a section below that plane at a distance from it which is the same, but in the other direction, as that of the first section.
The first section (hexagon) represents the six 'nothern' faces of the trapezohedron.
The other section (hexagon) represents the six 'southern' faces of the trapezohedron.
See Figure 8.
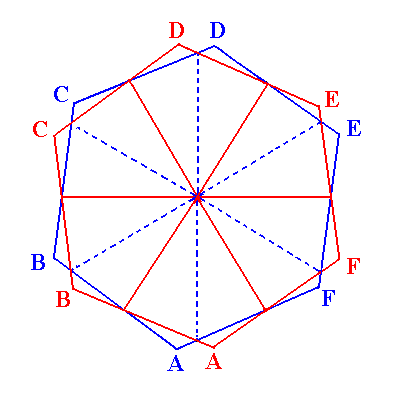 |
Figure 8. The two regular hexagons resulting from the superposition. |
When these faces are allowed to extend they will meet as indicated in Figure 4, forming the hexagonal trapezohedron.
From the holohedric hexagonal protoprism we can derive the trapezohedric hemihedric type I hexagonal prism by applying trapezohedric hemihedric to it. The prism does not change its external shape, as can be seen in Figure 9, but looses symmetry, because all the mirror planes are suppressed.
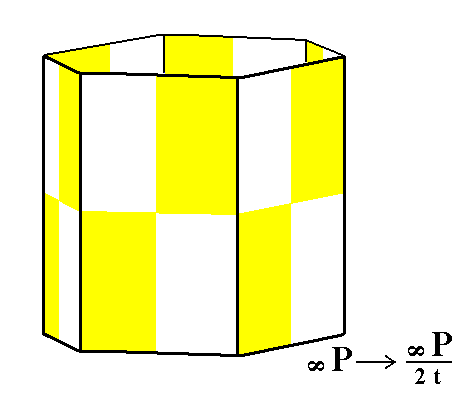
Figure 9. Derivation of the trapezohedric hemihedric Type I Hexagonal Prism from the holohedric Hexagonal Protoprism by suppression of all the mirror planes.
From the holohedric hexagonal deuteroprism is derived the trapezohedric hemihedric type II hexagonal prism by applying the trapezohedric hemihedric to it. As can be seen from Figure 10 the external shape remains unchanged, but the symmetry is lowered.
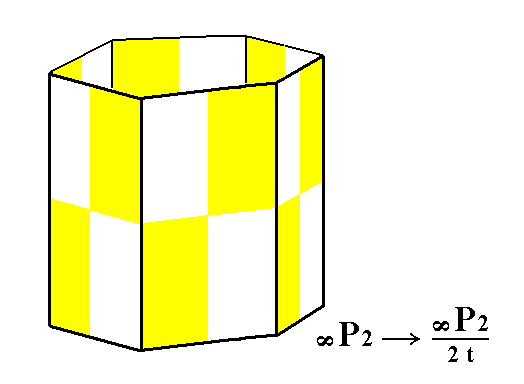
Figure 10. Derivation of the trapezohedric hemihedric Type II Hexagonal Prism from the holohedric Hexagonal Deuteroprism by suppression of all the mirror planes.
From the holohedric dihexagonal prism is derived the trapezohedric hemihedric dihexagonal prism by applying the trapezohedric hemihedric to it. As can be seen from Figure 11 its shape remains unchanged, but the symmetry is lowered.
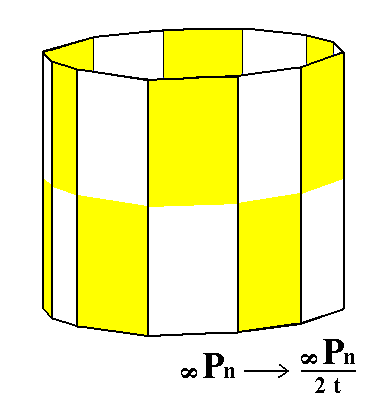
Figure 11. Derivation of the trapezohedric hemihedric Dihexagonal Prism from the holohedric Dihexagonal Prism.
From the holohedric basic pinacoid is derived the trapezohedric hemihedric basic pinacoid. So also in this case the new Form assumes the same shape but its symmetry is lowered.
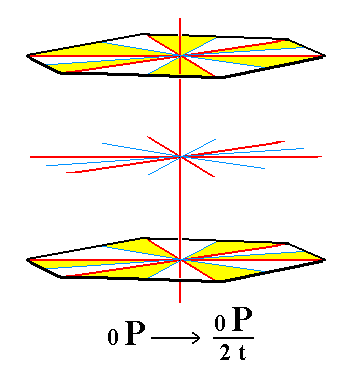 |
Figure 12. To obtain a trapezohedric hemihedric Basic Pinacoid we must (as for obtaining any trapezohedric hemihedric Form) drop all mirror planes of the corresponding holohedric Form. The suppression of all the vertical mirror planes is expressed by the colored areas of each face. The suppression of the equatorial mirror plane is expressed by the fact that each yellow area of the upper face has a white area directly below it on the lower face, and each white area a yellow one. |
This concludes our derivations of all the Forms of the Hexagonal-trapezohedric Crystal Class.
All these Forms can combine in real crystals.
FACIAL APPROACH
We will now derive those same Forms by subjecting the basic faces (compatible with the Hexagonal Crystal System) one by one to the symmetry operations of the present Class (the Hexagonal-trapezohedric Crystal Class).
In Part One we found the following seven basic faces compatible with the Hexagonal Crystal System :
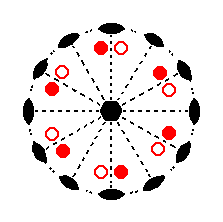 |
Figure 13. Stereogram of the symmetry elements of the Hexagonal-trapezohedric Crystal Class, and of all the faces of the most general Form. The periphery of the stereogram (i.e. the circle bordering the plane of projection) is dashed, meaning that there is no equatorial mirror plane. The same is the case with respect to all vertical mirror planes. So the 2-fold axes (symbolized by small solid ellipses) do not lie in any mirror plane, nor are they perpendicular to any of them, because there aren't any mirror planes. |
The face a : ~a : -a : c will give rise to a trapezohedric hemihedric type I hexagonal bipyramid when subjected to the symmetry elements of this Class : First the face will be multiplied six times by virtue of the 6-fold rotation axis. The result will be a type I hexagonal monopyramid. Further, to each of these six faces, when subjected to the 2-fold rotation axis that goes right through it, will be added a counterface intersecting the c axis at its opposite end, opposite when compared with the c intercept of the face that was initially subjected to such a rotation. See Figure 14.
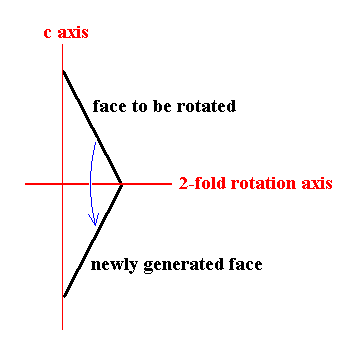 |
Figure 14. 2-fold rotation (i.e. rotation of 1800 about the axis) of a face intersecting the c axis. A second face is generated, intersecting the c axis in the opposite direction. |
This 2-fold rotation should not be confused with a reflection (mirror plane) as the next Figure illustrates.
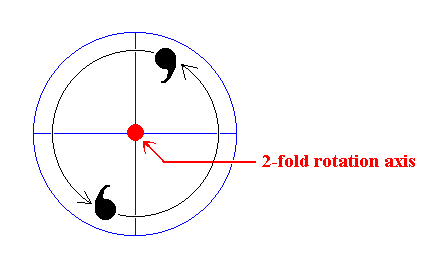
Figure 15. 2-fold rotation of a motif generates a second motif (resulting in the fact that the set, now consisting of two motifs, has 2-fold rotational symmetry).
As can be seen such a rotation does not generate reflectional symmetry, i.e. the motifs are not related to each other by a mirror plane.
So each of the six faces will be associated with a counterface by virtue of the 2-fold rotation axes. The result will be a type I hexagonal bipyramid.
The position of the initial face and the generation of the corresponding Form is depicted stereographically in Figure 16.
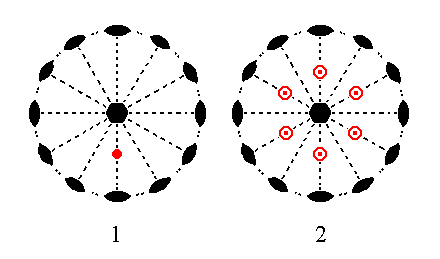
Figure 16. (1). Position of the face a : ~a : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the trapezohedric hemihedric Type I Hexagonal Bipyramid.
The face 2a : 2a : -a : c generates a trapezohedric hemihedric type II hexagonal bipyramid when it is subjected to the symmetry elements of this Class. The face will be multiplied six times in virtue of the 6-fold rotation axis. Each of the six resulting faces will be duplicated resulting in an upper and a lower face as was the case above. The result is a type II hexagonal bipyramid. See Figure 17.
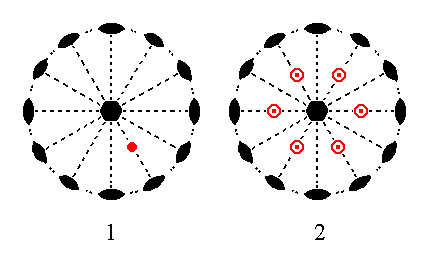
Figure 17. (1). Position of the face 2a : 2a : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the trapezohedric hemihedric Type II Hexagonal Bipyramid.
The face [3/2]a : 3a : -a : c is a definite face. It will give rise to one of the possible general Forms, i.e. a Form generated from a face -- like our just mentioned definite face -- that does not have a special orientation with respect to any symmetry element or any crystallographic axis. We will however treat the generalized version of this face, namely the face [s/(s-1)]a : sa : -a : c. Its position and the generation of the corresponding Form is depicted stereographically in Figure 18.
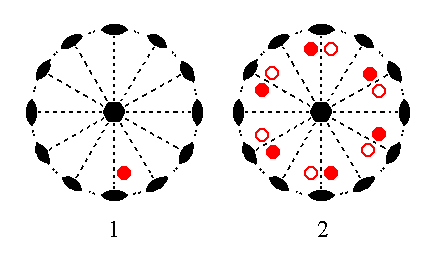
Figure 18. (1). Position of the face [s/(s-1)]a : sa : -a : c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Generation of the Hexagonal Trapezohedron in stereographic projection.
In producing this Form -- the hexagonal trapezohedron -- the face can be imagined first to be subjected to the action of its nearest 2-fold rotation axis. Because our face has a general (i.e. not a special) orientation with respect to that 2-fold axis (as it has to any axis) the new face generated by that axis will not end up precisely below the initial face as Figure 15 shows (in this Figure we look in the direction of this 2-fold rotation axis). The resulting face pair will of course have a 2-fold rotational symmetry, like for instance the letter S, but will not possess any mirror symmetry. The members of this face pair are a little bit displaced with respect to each other, i.e. the (generated) lower face does not lie precisely (and symmetrically) below the other. Next this face pair is multiplied six times around the c axis in virtue of the 6-fold rotation axis coinciding with it. The result is a hexagonal trapezohedron (See also Figure 4) .
The face [3/2]a : 3a : -a : ~c is like the previous face, except that it is vertical. We will treat its generalized version, namely the face [s/(s-1)]a : sa : -a : ~c. The action of the nearest 2-fold rotation axis will also in this case generate a second face. But because this face, and also the initial face, is vertical there is no differentiation into upper and lower faces. The initial face extends downwards, and the newly generated face extends upwards. So we end up with a vertical face pair. This face pair is then multiplied six times around the c axis in virtue of the 6-fold rotation axis coinciding with it. The result is a trapezohedric hemihedric dihexagonal prism. The position of this face and the generation of the corresponding Form is depicted stereographically in Figure 19.
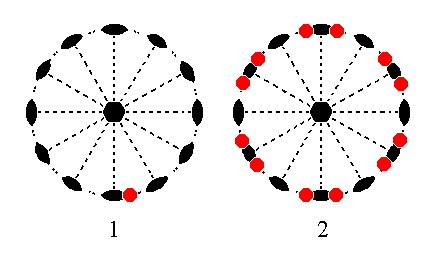
Figure 19. (1). Position of the face [s/(s-1)]a : sa : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the generated trapezohedric hemihedric Dihexagonal Prism.
The face a : ~a : -a : ~c is also vertical, but with a special orientation with respect to the crystallographic axes : It is parallel to the a2 axis. When we subject this face to its nearest 2-fold rotation axis, namely the one going right through it, i.e. lying perpendicular to it, no new face is generated. So we'll end up with that same face. When this face is then subjected to the action of the 6-fold rotation axis it will be multiplied six times, and the result will be a trapezohedric hemihedric Type I hexagonal prism. See Figure 20.
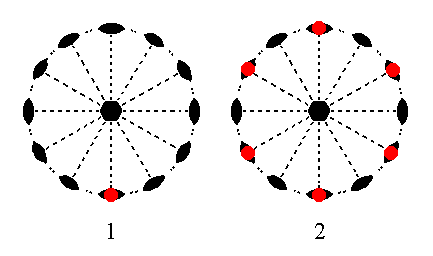
Figure 20. (1). Position of the face a : ~a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the trapezohedric hemihedric Type I Hexagonal Prism.
The face 2a : 2a : -a : ~c is also vertical. It is also special in its orientation with respect to the crystallographic axes : It cuts off equal pieces of two of them. Also here there is a 2-fold rotation axis perpendicular to it. So the action of this axis does not generate a new face. So also here we'll end up with that same face. When this face is then subjected to the action of the 6-fold rotation axis a trapezohedric hemihedric Type II hexagonal prism results. See Figure 21.
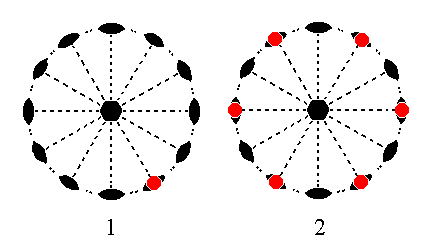
Figure 21. (1). Position of the face 2a : 2a : -a : ~c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the generated trapezohedric hemihedric Type II Hexagonal Prism.
Finally the face ~a : ~a : ~a : c is a horizontal face. The action of the 6-fold rotation axis does not produce new faces. But the action of any one of the horizontal 2-fold rotation axes (all lying in the equatorial plane) produces a second face parallel to the initial one. So we end up with a Form consisting of two horizontal parallel faces, a trapezohedric hemihedric basic pinacoid. See Figure 22.
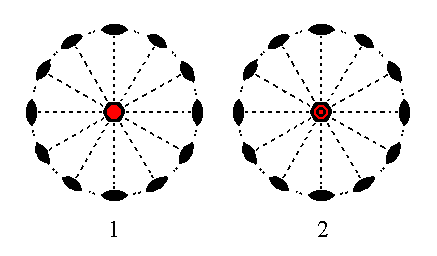
Figure 22. (1). Position of the face ~a : ~a : ~a : c in the stereographic projection of the symmetry elements of the Hexagonal-trapezohedric Crystal Class. (2). Stereogram of the generated Basic Pinacoid.
This concludes our exposition of the Hexagonal-trapezohedric Crystal Class.
To continue, klick HERE for Part Six (Class 3* 2/m).