
L-systems
back to homepage
Introduction
L-systems (Lindenmayer-systems) are Artificial Life systems (running on a computer) that generate -- like all untill now developed artificial life systems -- (only) some aspects of life.
In computer-based artificial life systems the general strategy is bottom-up programming. This means that the life functions must emerge from the interactions of elements (interacting and situated) at a low level (bottom). They must accordingly not be pre-programmed (top-down programming). Since it is effectively impossible to cover every conceivable situation in a top-down programming, top-down systems are forever running into combinations of events they don't know how to handle, so they are fragile and can easily grind down to a halt in a dither of indecision.
The same kind of bottom-up approach is applied to the graphical plants (or plantlike animals) of Lindenmayer. These plants are not drawn on the computerscreen, but grown. They start from a single stem, or some other simple morphological element, and build themselves up by applying a set of simple Rules. These Rules do not say anything about the final shape of the plant. The morphology of this final plant is just emerging from these Rules.
Description of L-systems
An L-system is a (computer) model for generating organic forms from a simple Rule Set and a simple initial form. In fact they are systems for manipulating symbol strings, resulting in certain complex symbol strings. The latter are then translated into strings of drawing commands, and the drawing commands are then consecutively executed, resulting in computer screen images.
Just like a CA (See the Essay on CA's ) or a RBN (See the Essay on RBN's ) an L-system is abstract. It is abstract also after interpretation of the symbols in terms of drawing commands (see below), because the resulting drawing on the computer screen can have no intrinsic interpretation, connecting it to the Real World.
Let me explain this.
Although L-systems (finally) generate recognizable (plantlike) images on the computer screen (while CA's and RBN's generally do not), those images never are, and never were, intrinsically, i.e. causally connected with real-world patterns. This in contradistinction to natural signs, namely concepts of real-world patterns. The formation of those concepts is ultimately caused by those real-world patterns. So they admit of an intrinsic interpretation in terms of real-world patterns.
The 'plants' of L-systems only have an 'after the event (has already taken place)' connection with real plants, i.e. just an extrinsic connection.
So also an L-system is an Ideal system and as such belonging to the Ideal Sphere of Being [ However, taken just in itself, but together with its interpretation (by the drawing commands) resulting in the morphology on the computer screen -- to which the formal system is geared -- it could be interpreted as a Totality-generating system. The generated Totality (i.e. a Being) only exists within the computer environment but is nonetheless real, because it is, in its computer screen interpretation (i.e. after the execution of the drawing commands), associated with material structures (the hardware of the display system of the computer). We should however realize that the connection of the (generated) pattern (i.e. of this particular pattern as such) with the computer display hardware is not of an intrinsic nature. It is like a song that is recorded on a CD, where the CD is the material substrate of the song.].
L-systems, despite their non-intrinsic interpretation in terms of the world outside the computer, can -- like CA's and RBN's -- give us much insight into the workings of Real dynamical systems.
An L-system (Lindenmayer-system, called after its discoverer) is a formal grammar by means of which symbol strings can be generated, just like we can form English sentences by means of the English Grammar (= rules for using the English language).
An L-system starts with the specification of a few constants, and then posits an initial string, for example AB. Such a start string is here called an Axiom.
Then one or more transformation rules are specified (these represent the grammar-type), by which letters (and/or other signs like #, &, ?, % etc.) can be substituted, for example A becomes AB, or by which letters etc. are removed, for example ACD becomes AD (i.e. C will be removed wherever it is encountered). In this way all kinds of transformation rules can be invented. Let me give some more examples :
- C becomes ADDW
- D becomes RRT
- R becomes A
- K becomes KSSD
- G becomes GGG
To the Axiom the whole list of specified rules (the rule set) will be applied. We then obtain a new symbol string. Then the same rule set will be again applied to that new symbol string. We then obtain yet another symbol string on which again the same rule set will be applied, et cetera. We can decide for ourselves how long we will continue this procedure.
Just like the CA's and RBN's, L-systems are recursive systems. In this way a, sometimes long -- often consisting of more then 1000000 symbols (letters and, depending on the type of system, other symbols) -- symbol string is produced. This string we call the Product string.
Then the symbols-of-this-string-together-with-their-sequence-(=relative positions)-in that-string are being interpreted as so called Turtle Commands, i.e. drawing commands. Consequently a drawing is generated. So an information-preserving transformation takes place FROM the computed Product string TO a drawing on the computer screen. What becomes visible are all kinds of plant-like or arthropod-like forms, sometimes very realistic.
L-systems are used for simulations of macroscopic organic form-generation.
An example of a very simple L-system, without a transformation into drawing commands, is the following (adapted from David GREEN, on the Internet) :
Fibonacci L-system
- Symbols : A, B
- Start string (Axioma) : A
- (grammatical) Rule 1 : A must be replaced by B
- (grammatical) Rule 2 : B must be replaced by AB
The Transition Law consists of two rules, Rule 1 and Rule 2.
The initial string is A.
Each process step consists in applying both rules. But of course in cases where only one of them is in fact applicable, we only apply that one rule.
So when we start with having A, then Rule 2 is not applicable because there is no B (which should be replaced by AB, according to Rule 2), so only rule 1 will be applied.
However, if we read the rules as follows :
Rule 1 : A must be replaced by B, if A is present (And wherever A is present in the string, the rule should be applied).
Rule 2 : B must be replaced by AB, if B is present (And wherever B is present in the string, the rule should be applied),
then we can simply say that the whole set of rules, namely Rule 1 and Rule 2, is being applied.
In whatever process step (= application of Rule 1 and Rule 2) the individual members of this rule set should be applied only once :
Suppose that we have BAB, and apply the rule set to it. We first apply Rule 1, resulting in BBB.
Next we must (in order to complete the process step) apply Rule 2.
Rule 2 says that B must be replaced by AB (if B is present). Accordingly we must apply Rule 2 to the first and third B, but not to the second B.
So the result will be ABBAB (and not ABABAB).
The next process step will proceed along the same lines. Each process step consists, as has been said, of the application, first of Rule 1, then of Rule 2.
Now we have sufficient knowledge about how to use the rules.
When we are going to run this (Fibonacci) L-system (i.e. the mentioned prescription, algorithm, or grammar) we will obtain the following process states :
A (axioma)
B (rule 1)
A B (rule 2)
B A B (rule 1, rule 2)
A B B A B (rule 1, rule 2)
B A B A B B A B (rule 1, rule 2)
A B B A B B A B A B B A B (etc.)
B A B A B B A B A B B A B B A B A B B A B (etc.)
After having applied the set of rules seven times, we now have obtained the Product string, which reads :
B A B A B B A B A B B A B B A B A B B A B
We can prolong this process as long as we wish to, by continually applying the rule set to the preceding result.
When we now count the number of symbols in each string of the above series of results, then we have the famous Fibonacci-sequence :
1, 1, 2, 3, 5, 8, 13, 21, etc.
This number series starts with two ONES, and then each next number is found by addition of the two preceding numbers.
This number series plays an important role in the morphology of many plants.
Shrimp
In the following I show an example of a much more complex L-system, that generates a long Product string. This string will then be interpreted as a drawing command, and the subsequent drawing is given. The system is run within a program called L-system Parser/Mutator, available on the Internet. Let's see how things unfold :
L-System Parser/Mutator v4.0
---------------------------------------------------------
Copyright (C) : RenderStar Technology BV. 1992-1995
Release date : Dec 27 1995 (386+/DOS)
---------------------------------------------------------
Sizing memory
L-system file : .\ lsys00n.ls
Recursion depth: 12 (This means that the set of rules is applied 12 times consecutively to the last (previous) generated result)
Basic angle : 10
Thickness : 100
Axiom : [c|H]AP[CD][?(1.6)U]
Rule : U=F+(5)U
Rule : A=[?(1.4)F]F?(0.6)F?(1.7)
Rule : D=[+(5)F+(5);(0.1)DGI]
Rule : I=ccc>>>>>>>>>[Tcc++++F][Occ----F]
Rule : G=Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Z
Rule : P=FQ
Rule : Q=[cc^^^^^^^^^MN][cc&&&&&&&&&MN]
Rule : M=F+?(0.95)M
Rule : N=L--L
Rule : C=F[R][E]+(5)C
Rule : E=cZ!E
Rule : R=[cc^^^^^^^^^BL][cc&&&&&&&&&BL]
Rule : B=:F+!B
Rule : L=[cc{--z++z++z--|--z++z++z}]
Rule : H=[^^^S]%[^^^S]>>>H
Rule : S=Z!S
Rule : T=Z+^!:T
Rule : O=Z-^!:O
Size of string : 4068 chars
Production (product string) :
[c|[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!Z!S]%[^^^Z!Z!Z!Z!S]>>>[^^^Z!Z!Z!S]%[^^^Z!Z!Z!S]>>>[^^^Z!Z!S]%[^^^Z!Z!S]>>>[^^^Z!S]%[^^^Z!S]>>>[^^^S]%[^^^S]>>>H][?(1.4)F]F?(0.6)F?(1.7)F[cc^^^^^^^^^F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)M[cc{--z++z++z--|--z++z++z}]--[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)F+?(0.95)M[cc{--z++z++z--|--z++z++z}]--[cc{--z++z++z--|--z++z++z}]][F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!cZ!E]+(5)F[[cc^^^^^^^^^:F+!B[cc{--z++z++z--|--z++z++z}]][cc&&&&&&&&&:F+!B[cc{--z++z++z--|--z++z++z}]]][cZ!cZ!E]+(5)F[[cc^^^^^^^^^BL][cc&&&&&&&&&BL]][cZ!E]+(5)F[R][E]+(5)C[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)[+(5)F+(5);(0.1)DGI]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Tcc++++F][Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Tcc++++F][Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]Z?(0.9)Z?(0.8)Z?(0.7)Z?(0.7)Z?(0.7)Z?(0.5)Zccc>>>>>>>>>[Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Z+^!:Tcc++++F][Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Z-^!:Occ----F]]][?(1.6)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)F+(5)U]
Datafile : output.vol
Objects : 3582
End
The graphics (= drawing on the basis of the product string) resulting from running this system looks like this :
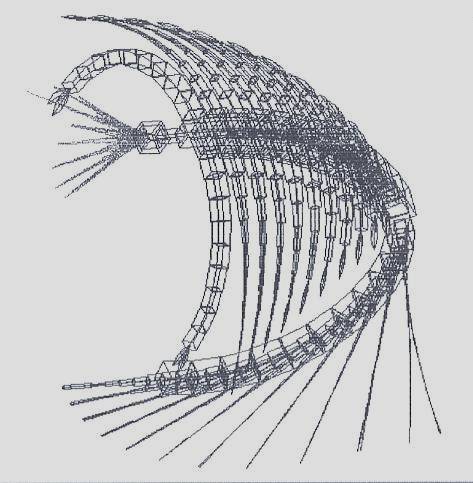
The image looks like a kind of Shrimp. In fact, when seen on the display utility of the L-parser, the image is 3-dimensional and in color. One can inspect it from any chosen direction.
To give a flavor of a sophisticated display of (another) arthropod-like creature, generated with the L-parser, click on the small image ( The image is taken from Laurens Lapré's Homepage about his L-parser, a sophisticated L-system program. )

Plant
Here's yet another example of an output of an L-system.
The image looks much like a plant.

The Dynamical Law in L-systems
L-systems can generate organic forms, and this (among others) by the fact that letting the system have a sufficient recursion depth (= number of times that the rule set is applied), structure-elements can be formed in which smaller copies of themselves can be built in, and IN those inbuilt structure-elements still smaller copies can be built in, etc.
Of course there is no direct parallel between L-systems and the organisms of which they can simulate their (outer) forms. The only thing L-systems show is that a simple linear symbol string ( linear, because we can think of the transformation-rules all written after each other) can code for a form [ in two or three dimensions -- the L-parser-shrimp-image above is in fact a three-dimensional image, seen from a certain angle], and this reminds us of DNA where we also see a linear string of instructions that can be read and executed. Much more correspondence than this does not however exist.
But it remains very remarkable that a small set of rules is in principle able to generate a very large and complex Product string, like we saw above.
It is, according to me, possible to interpret the posited constants + rule set as the Dynamical Law of the L-system, while the Axiom (the posited start string) can be interpreted as the initial state of the system. This Axiom is posited, and accordingly comes -- with respect to its configuration -- from outside the system.
The Recursion Depth is the number of iterations (number of times the rule set is applied) to which the Axiom is subjected. And that determines how long the system will run, and how many substructures will be built in within the final image.
So also in this type of model (of a dynamical system) one can clearly point to a Dynamical Law.
The Product string follows from the constants + Rule set + Axiom + Recursion depth, and consequently is less fundamental than the Dynamical Law.

The Garden of L. All of the plants were generated by L-systems and then rendered in three dimensions by computer-graphics techniques. The sky was created with a fractal algorithm.
( From LEVY, 1992, Artificial Life )
back to homepage
****************




