



Remark: In this Essay we will sometimes use powers of numbers. When a number is brought to the power of n, this means that that number must be multiplied n times with itself. When a particular power is indicated with a negative number, say -n, then that means also that the number must be multiplied with itself n times, but after this multiplication we must take the reciprocal value of the multiplication result. The resulting number is still positive (when the original number was positive). The convention adopted here on this webside for the notation of powers is the usual :
The number A to the n-th power is denoted as An.
A + 2X becomes 3X.
The kinetic equation, describing the variations of concentration of substance X, then looks like this :
dX / dt = kAX2.
This equation is accordingly not linear. Also without an autocatalytic step non-linearity of a kinetic equation could be the case, for example in the reaction :
2X becomes A
(See PRIGOGINE & STENGERS, 1989, p. 70), but that is barely sufficient for a possibility of generating macroscopic patterns.
Thus in the case of chemical reaction systems two conditions must be satisfied for them to be able to generate macroscopical structures :
What these systems are all about is the variation of concentration of one or more chemical substances participating in or produced by the reaction. We shall call the change in concentration of substance X in (the course of) time : dX / dt, and when this concentration remains constant (which would be the case when the system finds itself in a stationary state with respect to substance X), then dX / dt = 0 applies.
Let us first consider a simple chemical reaction ( different from the Brusselator, which we will consider hereafter and which is a model of a chain of reactions, one of which is an autocatalytic reaction step ) :
A + X becomes B + Y
This is a reaction equation.
Remark: The equation is in this case not specified. A real reaction equation could (for example) read as follows : NaCl + AgNO3 becomes AgCl + NaNO3.
(We shall confine ourselves to the reaction going to the right -- in most cases the reaction can proceed in the other direction as well, until equilibrium is reached. So in most cases we have to do with two reactions).
The reaction takes place by the collision of molecules. Only a small fraction of these collisions, for example 1/1000000, will result in a reaction and thus the production of B and Y from A and X. The reaction kinetics are described with differential equations which relate to the changes in concentrations, to be precise the rate of change of these concentrations. This rate of change is dependent on (i.e. proportional to) the concentration of the reacting substances. With respect to the above reaction equation the rate of change of the concentration of substance X, namely dX / dt, is thus proportional to the (arithmetical) product of the concentrations of A and X in the solution (i.e. the solution in which these substances find themselves, dissolved), and so we get :
dX / dt = -kAX
in which A and X now stand for the concentrations of substance A and of substance X, and in which k stands for the proportionality factor which relates to quantities as temperature and pressure and which provides a measure for the fraction of reactive collisions which do occur and which lead to the reaction
A + X becomes B + Y.
dX / dt = -kAX is a differential equation describing the kinetics of the reaction, and as such it is the Dynamical Law governing the reaction system.
Remark: In this case (and in likewise cases) this " dynamical law " is NOT the ultimate dynamical law, (ultimately) responsible for the formation of the macroscopic pattern (which we can loosely identify with a uniform thing, or Totality ). The ultimate law is located in the relevant properties of all the atoms that together build up the pattern, because we can consider the atoms as the ultimate constituents of the generated pattern, by reason of the fact that the atomic species do not change in such reactions, i.e. they are not changed into other species (See the Essay on the Determinations of a Substance, in the section on The Nature of the Elements ...). This ultimate dynamical law is identified with the Essence of the generated pattern.
But the equation
dX / dt = -kAX,
as given above, is a generic law. When A and X are specified we get a specific law, and only then it represents the dynamical law, i.e. the penultimate law, identifiable with the Essence of the generated pattern. The ultimate law resides on the level of atoms, as has been said.
k represents, in a way, the external conditions and co-determines the velocity of the reaction. We may stir the reaction mixture. When we don't do this, then we must take into account the diffusion rates of the substances involved.
A becomes X
2X + Y becomes 3X
B + X becomes Y + D
X becomes E
The second step is autocatalytic.
The product X, being produced from A and broken down to E is, via cross-catalysis, co-responsible for the production of Y.
X is being produced via a tri-molecular step from Y, but conversely Y is being formed in the reaction between X and a substance B.
In this reaction chain the focus of attention relates to the concentration dynamics of the (intermediary) substances X and Y. The concentration of A is held constant (because A is being consumed it must constantly be supplied to the system) and the behavior of the system is being investigated for increasing values of B (one value for each ' experiment '). Because of the supply of A and B (and removal of D and E) the system is held in a state of non-equilibrium. The initial and end products A, B and D, E are held constant during the reaction (i.e. during each individual ' experiment ') by means of the mentioned supply and removal, while the two intermediary components X and Y can have concentrations varying in time.
The kinetic equations for this system (corresponding to the above reaction equations) can (if we set the kinetic constants k, k', etc. equal to 1) be expressed in the form of a set of coupled differential equations which describe the changes in concentration of X and Y. They read :
dX / dt = A + (X2)Y - BX - X
dY / dt = BX - (X2)Y
This set of coupled equations thus represents the dynamical law governing the mentioned reaction system.
Because in the present case it concerns continuous variables (the concentrations of the participating substances) the dynamical law has the form of (a set of coupled) differential equations, in contrast with laws like Xn+1 = BXn, which describe a discrete process.
Remark: "Xn+1 = BXn" means the relation between successive states (process-stadia), always separated by a finite (in contrast with infinitely small) time interval : The state of X at time n+1 is B times the state of X at time n.
Differential equations relate to successive infinitely small increases or decreases (over infinitely small time intervals). When we want to deduce from these equations the behavior of the system, then all those infinitely small increases and/or decreases must be added together with the help of a technique called integration. Thus by integration of the dynamical law (in the present case the set of coupled differential equations) we find the behavior of the system.
Remark: The above is formulated in an epistemological way, i.e. relating to how to acquire knowledge (of the behavior). Ontologically [i.e. how things ARE, in themselves apart from being known] these equations -- as a dynamical law -- are 'existing' in a corresponding real dynamical system, but not necessarily in the mathematical form as presented by human investigators, whereby their correctness is of course presupposed, meaning that these formulated and mathematically expressed equations are equivalent to their ontological correlate.
When for example we want to know the concentrations of X and Y, prevailing in the Brusselator reaction system, when that system has evolved to a stationary state (= a state that does not change anymore), thus when dX / dt = dY / dt = 0 applies, then we substitute this value (the value 0) in the kinetic equations (the above differential equations), i.e. there we replace the expression dX / dt by 0, and dY / dt also by 0. Now we can solve the equations (integration) for X and Y and we so obtain : X = A, Y = B/A. These are accordingly the concentrations that prevail at a stationary state of the system.
If the identities of A, B, D, E, X and Y are explicitly determined, i.e. what substances are represented by A, B, etc., and then as such appear in the set of differential equations, then this set represents the specific dynamical law of the system in question. It then represents the Essence of the generated pattern (if such a pattern is indeed generated). With this the diffusion properties (expressed in diffusion coefficients) and also other relevant properties are directly implied and as such given ( The spontaneous faster or slower spatial expansion of some substance in a medium is called " diffusion " ). The diffusion itself also is a regular (= proceeding according to a law) phenomenon, it follows ' Fick's Law ', relating the concentration of a substance at a determined location in space with its change in time, for each substance present in the reaction mixture. The conversion factor in Fick's Law, which so relates, is the diffusion coefficient, which is a property of the chemical substance in question. All this accordingly appears in the equations when we completely specify A, B, D, E, X, and Y. Thus a term from Fick's Law has yet to be added to the dynamical law when we want to express the s p a t i a l events in the reaction mixture (See COVENEY & HIGHFIELD, 1995, Frontiers of Complexity, p. 163).
But let us first confine ourselves to a Brusselator reaction that is strongly stirred, in which we consequently do not have to account for (differences in) diffusion, and in which we accordingly confine ourselves to the generation of a macroscopical pattern in time, namely oscillation.
We then are finally able to formulate things in a way that serves our purposes (which is the search for the status of the dynamical law as Essence of the generated pattern -- the non-living dissipative structure, representing a uniform thing), whereby we imagine the Brusselator to be a real chemical system. In the following formulation the symbols A, B, etc. are thought to be completely specified in terms of the specific substances and their relevant properties. When we speak about "at a certain temperature and pressure", we mean : finding itself in a certain interval of temperature and pressure. Let's now formulate :
IF the (chemical) substance A and the substance B are present (in a solution), at a certain temperature and pressure, and if the (other, in addition to the latter) relevant external conditions result in (1) the substances being (and remaining) well mixed (for example by stirring), and (2) the concentrations of A and B remaining constant (effected by a compensating supply), and (3) the concentrations of the final reaction products (implied as D and E by the chemism of A and B) also remaining constant (effected by compensating removal), THEN the reaction chain
A becomes X
is implied,
dX / dt = A + (X2)Y - BX - X
(whereby the symbols A, B, X and Y denote the concentrations of these substances)
STARTS TO OPERATE, and the dynamical evolution of the system begins.
2X + Y becomes 3X
B + X becomes Y + D
X becomes E
AND THE DYNAMICAL LAW --- with respect to the concentration evolution of the intermediary substances X and Y (also implied by the chemism of A and B)---
dY / dt = BX - (X2)Y
This set of coupled differential equations -- the dynamical law -- is the Essence of every macroscopical pattern generated by the Brusselator as specified above. Such a macroscopical pattern can represent a non-living uniform thing, a non-living Totality (meaning an intrinsic totality of constituents, and thus forming an intrinsic unity).
The concentrations of A and B together form the initial condition (start stadium) of the dynamical system, and they imply a start concentration of X and Y as soon as the reaction has begun, and because the concentrations of A and B are held constant during a run of the reaction, the concentrations of X and Y are the actual (the 'real') starting state (initial condition) of the system.
Remark : The being, generated by the Brusselator is, of course, not (yet) a full-fledged being. It is a pattern, and as such a precursor of such a being. Dissipative systems, as discussed here, are a prelude to genuine beings, especially to organisms.
As long as the relation B > (1 + A2) -- with respect to the concentrations of A and B -- does NOT apply [" > " means : bigger than ] the system (the Brusselator ) will, under the conditions mentioned, evolve towards a stationary state, in which the concentrations of X and Y do not change anymore. In that case the relations
X = A and Y = B/A
hold. But, when we are now going to increase the concentration of B (in a second experiment) -- and that means that we push the system further from equilibrium -- then, when B > (1 + A2) applies, this stationary state will become unstable. Now, in case of the smallest perturbation the system will consequently leave the stationary state. It will end up in another dynamical regime. In the present case it will end up in a stable limit-cycle.This means that the concentrations of X and Y will start to oscillate in a regular way. Thus instead of remaining constant the concentrations of X and Y will swing with a constant period. When we imagine for a while that the substance X is blue and the substance Y red, then the system will first be, say, totally red, then totally blue, then totally red, etc.
That this ordering (this organization) would be the result of the activities of billions of molecules seems unbelievable -- it concerns after all just a model for a dissipative chemical reaction chain -- but such phenomena are indeed observed in real chemical reactions.
The phenomenon just described is a certain form of self-organization, in the present case a macroscopic pattern in time, namely an oscillation. Such a phenomenon is called a ' chemical clock '.
In addition to a pattern in time the system is also able to generate patterns in space, and in space and time. This happens when diffusion comes into play. The diffusion-reaction equations of the Brusselator reveal a baffling assortment of possible behaviors of the system. The diffusion of chemical substances finding themselves in a far from equilibrium condition can lead to new forms of instability. It is then possible that vibrations (oscillations) will occur in time as well as in space. These are waves in the concentrations of X and Y, periodically traversing the system (PRIGOGINE & STENGERS, 1986, p. 148). The condition of being far from equilibrium can also lead to the system going in the direction of a new stable stationary state with an inhomogenous distribution of X and Y in the Brusselator reaction.
Remark: Because the state is now stationary nothing changes in time. Patterns in space are formed.
It is possible to indicate a determined wavelength in the stationary concentration bumps which is directly proportional to the spatial extension of the system. With this the macroscopical character of the emergent order is clearly expressed. Somtimes even a polarity of the structure appears (a high concentration of X at one end of the container) when the system is subjected to a disturbance (Something like this happens in the development of an embryo from a homogenous cellmass : there appears a gradient)(See JANTSCH, 1980. PRIGOGINE & STENGERS, 1986). See next Figure.
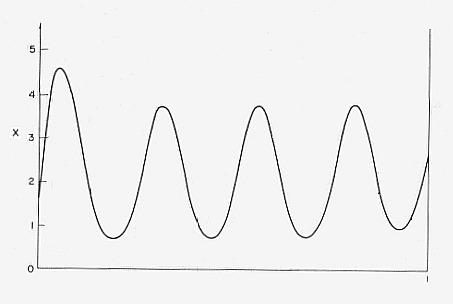
Figure 1. Formation of a stable dissipative structure far from equilibrium in the chemical reaction system " Brusselator ". The concentration of X was calculated under the following assumptions : A = 2, B = 4.6, DX = 0.0016, DY = 0.0080. ( DX and DY are the diffusion coefficients of substance X and Y respectively ). The higher concentration of X on the left side indicates spontaneous polarization. (The horizontal axis represents space in arbitrary units.)
( After Jantsch, 1980 )
If also the diffusion of the start-product A can no longer be ignored, dissipative structures can appear past a critical instability, whereby in this case the spatial organization (generated by the system) is limited to a determined volume (inside the system). Outside this volume the classical thermodynamical regime prevails. So in this case the Brusselator generates a pattern with intrinsic boundaries . See next Figure.
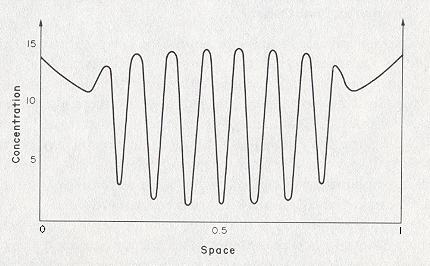
Figure 2. Formation of a localized dissipative structure in the chemical model reaction " Brusselator ". The concentration of X was calculated under the following assumptions : B = 26, DA = 0.197, DX = 0.00105, DY = 0.00526. ( DA , DX and DY are the diffusion coefficients of the substances A, X and Y respectively ). Outside the dissipative structure, the classical thermodynamic order reigns.
( After Jantsch, 1980 )
And here the size of the dynamical system is important with respect to the formation of dissipative structures (patterns). A system that is too small will always be dominated by boundary effects. Only above certain critical sizes the non-linearities will find a possibility to unfold their characteristics, and so bring with them novel structures (patterns), resulting in a certain autonomy of the system with respect to its environment. Not until then we can speak of the formation of a genuine Totality (distinguishing itself intrinsically from its environment, not until then it is an ' itself '). A dissipative structure (pattern) will only appear when a specific size is realized, but then there will be no difference in structure anymore between the case of the size (of the environment) being just sufficient and cases of much more larger sizes of the environment (except with respect to the 'life-span' of the system, being dependent on the environment with respect to 'food' in the form of free energy and a replenishment of reactants) (JANTSCH, 1980).
The Belousov-Zhabothinsky reaction itself is significantly more complicated than this idealized four-step process, but the basic principle remains the same. The reaction consists of two cyclic processes coupled together by the interconversion of one Cerium ion into another : Ce3+ and Ce4+. This interconversion can be monitored by the indicator Ferroin, which turns red in the presence of Ce3+ ions, and blue where Ce4+ ions dominate. The second of the two cyclic reactions just mentioned, is still not understood completely. The oscillations are caused by the alternating dominance of the two cyclic steps implying an alternation of the Cerium ions and thus an alternation of red and blue. The successive boost and inhibition of those reaction steps cause the chemical waves, visible as target patterns or spirals.
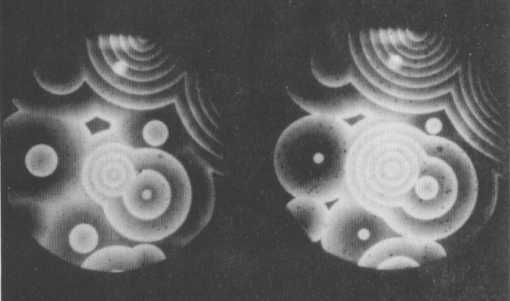
Figure 3. Target patterns formed by the Belousov-Zhabotinsky reaction
( After Coveney & Highfield, 1991, The Arrow of Time )
Chemical systems, related to the BZ-reaction, in which structures could form spontaneously in an autocatalytic system in which the reactant molecules diffuse at different speeds through the reaction medium -- are so-called reaction-diffusion systems (Also the BZ-reaction itself is such a system when the reaction is not stirred). In order to describe such systems I will quote a few passages from Philip BALL, 1994, Designing the Molecular World . Concerning reaction-diffusion systems he writes :
Specifically, if the faster-traveling reactants inhibit the reaction whereas the slower ones catalyze it, then within a certain range of diffusion rates of the reactants the system can transform suddenly from a uniform mixture into one in which the chemical composition varies in a regular manner from place to place. In effect, the system turns into a kind of crystal, with periodic structure -- but a very peculiar kind of crystal, because all the molecules within it are free to move around yet the patterned structure remains. In a normal crystal, this freedom of movement would destroy any periodicity.In general, autocatalytic reactions like the BZ-reaction tend to produce moving chemical waves, not stationary structures. These latter are seen for the first time in 1990 by Patrick de Kepper and colleagues from the University of Bordeau. Let's quote BALL again :
De Kepper's group studied a variant of the BZ-process, called the chlorite-iodide-malonic acid (CIMA) reaction, in which the reactants were mixed within a gel to slow down the diffusion rates so that stable patterns might form. The researchers used a starch-based indicator to reveal the changes in chemical composition throughout the system : the indicator turns either yellow or blue, depending on whether the concentration of the ion I3- [ an ion consisting of three iodine atoms in such a way that the net electrical charge is one negative unit (equivalent to the charge of an electron ], an intermediate species in the reaction, is high or low. They observed a few rows of yellow dots within a certain region of the otherwise blue gel, which they identified as Turing structures [ In the 1950's Turing had predicted such structures on theoretical grounds ]. Harry Swinney and Qi Ouyang of the University of Texas at Austin were later able to "grow" large patches of these Turing structures. At first the reaction produces radiating target patterns like those of the BZ-reaction, but over a period of an hour or so these patterns break up into regular hexagonal arrays of yellow dots which slowly come to rest [ See Figure 4 ]. By changing the temperature of the system, Ouyang and Swinney were able to transform their dot pattern into a stripe pattern -- this kind of transformation too had been predicted by Turing's theory.

Figure 4. Two-dimensional arrays of stationary Turing structures can be generated in the CIMA reaction under appropriate conditions of temperature and reactant concentration. A hexagonal pattern at one temperature (left image) changes to a stripe pattern at another (right image).
( After BALL, 1994, Designing the Molecular World )
The investigation of such self-organizing chemical systems is still going on. All these chemical systems, mainly variants of the BZ-reaction, strongly point in the direction of corresponding biochemical processes in Organisms, for example the aggregation patterns of the Slime Mold. This mold consists of amoebae (unicellular animals) living on the forest floor. When starved (i.e. finding themselves in unfavorable conditions) they aggregate into a multicellular body which can then move in search of a more favorable habitat. The aggregation is triggered by the release of the compound cyclic adenosine monophosphate (cAMP) from some of the amoebae (See Figure 5).
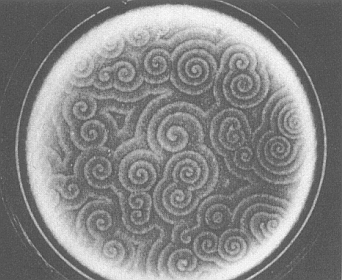
Figure 5. Spiral waves in colonies of the mold Dictyostelium discoideum. These patterns are created when the mold forms aggregates in response to some external ' stress', such as a lack of moisture or nutrients.
( After BALL, 1994 )
Also static patterns are observed in the natural world. For example in larvae of the fruit fly. In the early development the embryo evolves stripes which represent the evolving segments of the insect. This development is thought to be related to the concentration of a protein called Bicoid, which increases gradually from one end of the developing egg to the other. The concentration of the Bicoid protein provides a signal that switches on genes at different points along the body axis, dividing the embryo into a sequence of segments which will develop into different parts of the body (BALL, 1994). (See figure 6)

Figure 6. In the early stages of development, fruit fly larvae develop striped patterns. The regions of different shade represent parts of the embryo that will subsequently follow different developmental pathways. A gradual variation in the concentration of a morphogen called the bicoid protein from one end of the embryo to the other provides the chemical signal that stimulates this patterning.
(After BALL, 1994 )
In the just discussed development of the larva of the fruit fly we in fact saw the development of metamers or sequential parts. The potential metamers will develop partly into qualitatively the same or almost the same actual metamers, partly into qualitatively different metamers. So the final result is not just a linear repetition of identical structural elements, thus not something like a one-dimensional crystal, but is - what we earlier called - a tectological structure. And all this seems to be accomplished by certain dissipative subsystems (within the overall dissipative system that is represented by the whole developing organism in its environment). So the actions of such systems (including diffusion phenomena) can indeed account for the organism's
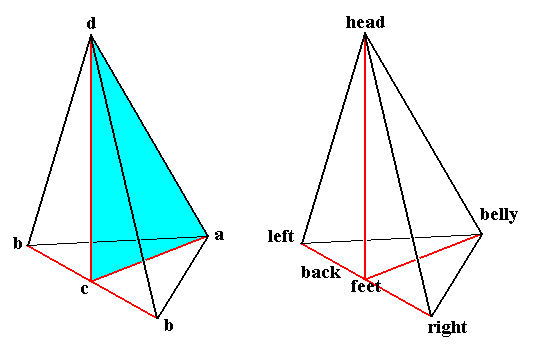
Figure 7. One half of a rhombic pyramid, as such indicating the axial relations of the Eudipleura (bilateral s.str. organisms).
The left image emphasizes the only mirror plane present. The right image names the poles of the three axes (the latter are indicated in red).
Many other organisms, like radiolarians, and medusae, or stages of them, like pollen grains and eggs, show different ideal stereometric forms, that can be represented geometrically by spheres, regular or irregular endospheric polyhedrons, or by ellipsoids, cones or by all kinds of pyramids, and hemipyramids.
So we see that, when studying non-living dissipative systems, we automatically end up at a contemplation of analogues in the organic world.
The patterns we see in reactions like the BZ-reaction can also be simulated in a computer by means of Cellular Automata (CA)(See Figure 8). These are simple, but of course abstract, dynamical systems governed by a certain rule by applying that rule again and again, i.e. the rule is recursively applied to its output (See for CA's the Essay on Cellular Automata).

Figure 8. CA-analogue of the BZ-reaction. The pattern (which is dynamic) is generated by the rule ZHABO.JC in the CA-simulator CELLAB of Rudy Rucker and John Walker.
Today's chemistry is as mathematical as you could like (some would say more so). But the " reductionist " approach to many-molecule systems, which tries to provide a description based on a few simple equations representing the interactions between molecules, becomes rapidly intractable as the numbers grow larger. The world therefore abounds with systems that have in the past been regarded as far too complex to permit any obvious means of realistic mathematical analysis. One of the astounding revelations of recent decades, however, is that complexity does not necessarily imply disorder, intractability or general messiness. Rather, it has become apparent that complexity can itself give rise to the abrupt manifestation of order, often in the form of patterns of startling richness that are a far cry indeed from the geometric sterility generally exhibited by simpler systems. The real surprise is that there may be nothing in the fundamental elements of the mathematical description to warn us that these structures might appear. A reductionist sees only the most prosaic of interactions between the system's individual components, but the " holist " who considers the system as a whole discovers within it an unguessed capacity for intricate organization.
Many of the patterns that arise out of complexity resemble the delicate and often beautiful " organic " forms of the natural world. Moreover, similar patterns may be found in systems that are ostensibly unrelated. There is a common thread, however : these systems tend to be undergoing processes of rapid or unstable transformation. This has lead to hopes for a unified description of pattern formation in systems that are far from attaining equilibrium.