(These links are only appropriate for readers who arrived directly on this particular page, i.e. not via the Homepage.)
At (9) in Figure 1 we stated that "a horizontal mirror plane is implied by the configuration of the motifs (i.e. the presence of lower motifs precisely below corresponding upper motifs) and by (i.e. combined with) their relation to the 2-fold axes".

Figure 1a.
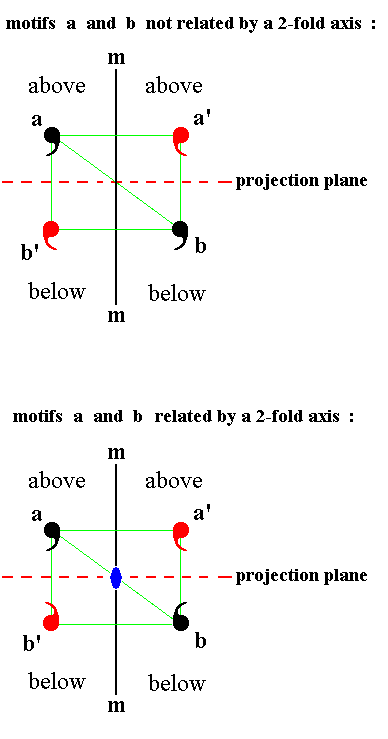
If we have a motif that lies right above a horizontal 2-fold rotation axis (this axis being perpendicular to the -- vertical -- n-fold axis, and lying in the projection plane), then the projection of the face pole representing it comes to lie right on the projection of that 2-fold rotation axis. Its rotational image comes to lie right below the 2-fold axis (and also right below the original motif), while its projection also comes to lie on the projection of the axis. The motif and its image are, however, not symmetrical with respect to the projection plane, in spite of the fact that in stereograms they together are depicted as a small centered circle whether symmetrical or not. See Figure 1b.
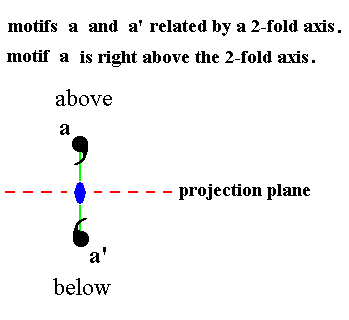 |
Figure 1b. Although a 2-fold rotation axis, lying in the projection plane and perpendicular to the plane of the drawing, can generate an image exactly below the initial motif, the two motifs, a and a', one above and one below the projection plane, are not necessarily symmetric with respect to the projection plane. The 2-fold rotation axis is indicated by a small blue solid ellipse. |
In our derivations (of the Crystal Classes) we do not have to do with situations like in Figure 1b, because the position of the motifs (represented by the projection of face poles) is always taken as a general position.
When we have, in a stereogram, two (projections of) upper face poles (Because they refer to real motifs, we often call them motifs too), at equal distances from the center of the projection plane and not lying on its perimeter, we depict that as two small solid red circles. If we add a 2-fold rotation axis lying in the projection plane, right between those (projections of the) two face poles, then two more face poles (respectively motifs) are generated, as can be seen in the next Figure.
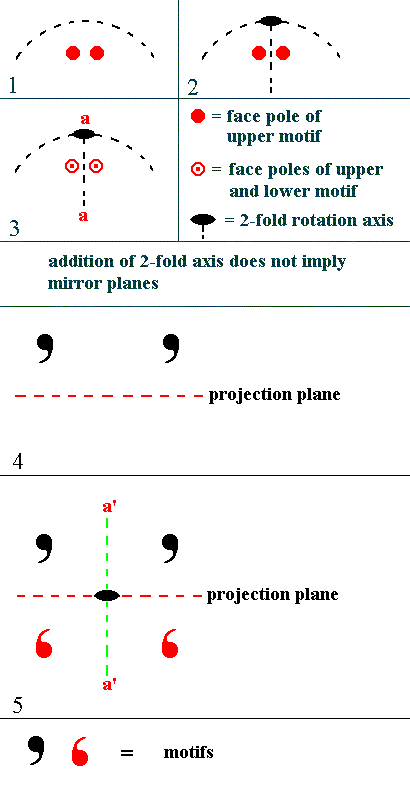
Figure 1c. Mirror planes not implied.
(1). Part of a stereogram showing (the projections of) two upper face poles at equal distances from the center of the projection plane.
(2). Addition of a 2-fold rotation axis lying in the plane of projection, and going right between the two projected face poles.
(3). The added 2-fold rotation axis generates two lower face poles lying right below the upper face poles. The total number of face poles is now four. There are, however, no mirror planes implied (neither a horizontal mirror plane, nor a vertical mirror plane (aa)), as the next images will show by means of real motifs.
(4). Two upper motifs (represented here by comma's), i.e. motifs whose projections first of all end up on the upper half of the projection sphere, from which they are then projected onto the projection plane, and then -- in stereograms -- depicted as small solid red circles. Now we are viewing not from the north pole of the projection sphere onto the projection plane, but from a direction perpendicular to that.
(5). A 2-fold rotation axis lying in the plane of projection is added. This axis generates two lower motifs. The total number of motifs is now four.
One can clearly see that no mirror planes are implied, neither a horizontal mirror plane (coinciding with the projection plane), nor a vertical mirror plane (a'a').
Implication of mirror planes
In (8) of Figure 1 (main document) we had the following situation (in the process of the derivation of G5 from D2) :
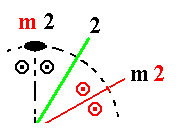
In (8) we stated that " the symmetry elements, now present, multiply the motifs resulting in a pattern as indicated."
In (9) we stated that " this motif pattern demands the presence of two more vertical mirror planes containing the 2-fold axes that had been indicated by the color green."
So the question is whether the resulting motifs are such that their configuration is symmetrical with respect to a plane, perpendicular to the projection plane and containing the 'green' 2-fold axis. As long as the motifs are referred to by (projections of) face poles, i.e. not by morphological figures (motifs) but just by points, dots or circles, a symmetry is, to be sure, suggested but not proven : Are the two sets of motifs (one set given in black, the other in red) symmetric with respect to the plane perpendicular to the projection plane and containing the green 2-fold axis? Indeed they are, as the next Figure illustrates. In this Figure we depict the same situation but now looking in a direction perpendicular to the direction of viewing in the case of stereograms. The dashed red line is the projection plane. We see the two sets of motifs (each containing four motifs, indicated by comma's) related to each other by a 2-fold axis, lying in the projection plane (and indicated by a larger solid ellipse provided with the numeral 2). A set of four motifs, as depicted here, can be interpreted as one symmetrical motif. And if such a symmetrical motif is rotated by 1800 about an axis lying in one of the mirror planes of the complex motif (here this mirror plane of the complex motif coincides with the plane of projection, the dashed red line), then we will obtain another such complex motif that is symmetrical with the original one with respect to a plane perpendicular to the projection plane and containing the 2-fold axis (= one of the green axes in the stereogams of Figure 1, that relates the two complex motifs with each other). This means that indeed the green 2-fold axis will be contained in a (vertical) mirror plane, and can then be denoted by the symbol m2. In the next Figure one can see that the two sets of motifs are not just symmetrical, they are congruent, which means that they are rotational images of each other. They are repeated six times, implying a vertical 6-fold rotation axis, and garanteeing that all the motifs, not only the ones just discussed, are symmetrically arranged with respect to the plane perpendicular to the projection plane and containing the green 2-fold axis. The same applies for the other green 2-fold axis and for the original (horizontal) 2-fold axis stretching from 9 o'clock to 3 o'clock in the stereograms. They can now be denoted by the symbol m2.
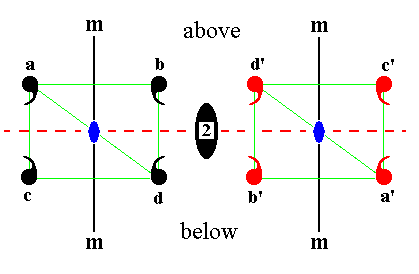
Figure 1d.
Effect of the 2-fold axis, indicated by a larger solid ellipse provided with the numeral 2, on a symmetrical complex motif.
a is mapped onto a', b onto b', c onto c' and d onto d'. The two resulting complex motifs, each consisting of four single motifs, are not only symmetrical, but also congruent.
The above case, just discussed, must, however, still be checked for the behavior of real motifs when viewed from above, i.e. with a viewing direction perpendicular to the projection plane (as we do in stereograms).
In Figure 1a we saw that two motifs, related to each other by a 2-fold axis and a mirror plane perpendicular to the projection plane, will be multiplied such that the resulting motif pattern is symmetric with respect to the plane of projection. When we look in the direction just indicated we then see two pairs of motifs, one lying exactly above the other (one above the plane of projection, the other below it). Another such double pair will be generated by the 'green' 2-fold rotation axis. We depict this situation in the next Figure, first by means of face poles, then by means of motifs (represented by those face poles). We want to know whether or not the original, and its image generated by that 2-fold axis, are symmetric with respect to the plane perpendicular to the plane of projection and containing the green 2-fold axis.
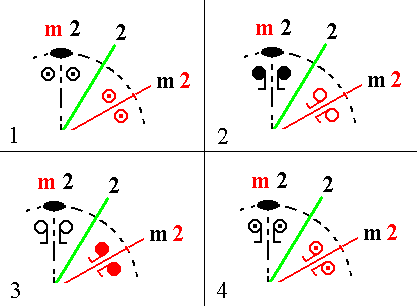
Figure 1e.
(1). Initial motif pair (double pair), represented by face poles, and its duplication by the 2-fold rotation axis (green).
(2). Two lower face poles, now given as (lower) motifs (open) are generated from the two upper face poles, now given as (upper) motifs (solid), by the action of the 'green' 2-fold rotation axis.
(3). Two upper face poles, now given as (upper) motifs (solid) are generated from the two lower face poles, now given as (lower) motifs (open), by the action of the 'green' 2-fold rotation axis.
(4). (2) and (3) combined.
In (4) of the above Figure we clearly see that the motif configuration is indeed symmetric with respect to the plane perpendicular to the projection plane and containing the green 2-fold rotation axis. Now we know for sure that a mirror plane is implied and that we accordingly can label (in Figure 1 of the main document) the green lines in the stereograms with the symbol m2.
(These links are only appropriate for readers who arrived directly on this particular page, i.e. not via the Homepage.)