
This supplementary approach should take into account items like boundaries, parts, inside, outside, discrete, disjoint, connectedness, continuous and contiguous.
It is especially important to consider the diverse relations between parts, resulting in the establisment of different kinds of boundaries, and consequently in (the establishment of) different kinds of wholes. Some boundaries are common boundaries and so do not exclusively belong to one part. Other boundaries are not common boundaries, for example the boundary between two billard balls which are in mutual contact with each other. In this case the boundary at which the balls are in contact, a boundary which is momentarily shared in common by the two balls, is not necessarily dependent for its existence on either ball. It can exist perfectly well even if one or the other is destroyed.
If we speak here of "necessarily dependent for its existence" then, in this context, this is not meant purely physical and causal (causal, with respect to efficient causes). It concerns the identity, the whatness, of the items in question, and we ask what is needed for them to be what they are. In this way, for example, a father depends upon a son or a daugther. Without them existing (or having existed) he is not a father at all. So a father is a complex entity, in this case an entity necessarily connected, in a special way, to one or more other entities discrete from him (i.e. from the human being in question).
Approaching Reality from this viewpoint of parts and boundaries will indeed represent a necessary supplementary consideration, which can be called the MEREOTOPOLOGICAL APPROACH to Ontology (i.e. to the theory of Being(-as-such)).
On expounding this approach I rely heavily on two articles, one by Barry SMITH, On Substances, Accidents and Universals : In Defence of a Constituent Ontology, in Philosophical Papers, 26 (1997), 105--127, and another by Barry SMITH & Berit BROGAARD, 2000, Sixteen Days : The Ontology of Fetal Development. Internet : http://wings.buffalo.edu/philosophy/faculty/smith/articles/embryontology.htm.
This mereotopological treatment first of all applies to the world as is captured by common sense, i.e. the mesoscopic world of more or less everyday objects. It does not address very large entities (like galaxies and galactic clusters, the structures of which should be understood in terms of gravity, but gravity is not yet fully understood), and, even less so, microscopic entities, especially quantum entities. Quantum entities demand a special treatment, which is carried out in the Essay on Metaphysics and Quantum Mechanics. This restriction in scope is not something to worry about very much because the mesoscopic Substances can be considered as the primary instances of Being, while quantum entities can be regarded as deficient beings, because they lack full determination.
While the dynamical systems approach incorporates the individual history of a Substance, i.e. the succession of system-states, a succession governed by a dynamical law, the mereotopological approach considers a Substance as a here-and-now entity, and consequently ignores any dynamics. Although some effort is undertaken to incorporate the time dimension into a mereotopological approach [ See HERE (Internet) for such an approach : Quantum Mereotopology, by Barry SMITH & Berit BROGAARD, 2000, inspired by a new interpretation of Quantum Mechanics ], I think the dynamical systems approach deals more adequately with the time dimension. So what we will pursue here -- as a supplementary approach -- is a here-and-now mereotopology. This mereotopology also pays hardly any attention to the important intrinsic / extrinsic relation, and to the kindred per se / per accidens relation, because these are not purely mereotopological relations. And most important, it does not concern PATTERN, and pattern-formation, especially it does not concern REPEATABLE patterns.
Mereotopology is accordingly an ontology based principally on here-and-now wholes, parts and boundaries, and their topological roles and relations.
When we apply this ontology to all kinds of (mesoscopic) objects we will notice that it fails to recognize Substances -- i.e. genuine Substances, as such conceptually developed throughout this website, namely genuine Totalities : It recognizes them, to be sure, but it also recognizes many non-Substances (non-genuine Totalities) -- namely aggregates -- as 'Substances'. Not until supplemented with the dynamical systems approach, it will yield the correct results, i.e. only then it recognizes, in an exclusive way, real Totalities, displaying a repeatable and intrinsic pattern (a pattern of parts).
However, on the other hand, it cannot be denied that the 'aggregates' recognized as 'Substances' by mereotopology alone, are not just any aggregate, but, in a way, wholes, be it wholes in a weakened sense.
For example mereotopology recognizes an arm, which is just cut off from a living human being (forgive me for such a macabre example), as a Substance. But in fact it cannot be a genuine Substance, because it does not represent a dynamical system, i.e. it cannot be interpreted as a state of a certain dynamical system. It lacks dynamic integrity. Moreover the arm, after it has been detached, directly starts to disintegrate, and so indicating its aggregate nature. Professor Barry Smith, an authority on mereotopological ontology, agrees with me on this point (personal communication). Nevertheless it is clear that such a (freshly) cut-off arm is not an aggregate just like that. In a sense (namely in the mereotopological sense) it is one subsisting whole, having its own connected outer boundary separating it from the rest of the world, especially from other such things. The same can be said of, say, a table (where the parts are attached to each other), and where the extrinsic nature (of the pattern 'table') is even more pronounced. But still a table is far from being just an aggregate, like, for instance, a heap of stones.
We will now assess more precisely what categories of subsistent discrete entities can be found in mesoscopic Reality, and which of those are recognized and distinguished by mereotopology all by itself. The latter can distinguish some major types of these entities on the basis of the nature of their external and internal boundaries, and consequently the (topological) nature of their parts. Mereotopology is accordingly a constituent ontology.
First of all we find subsistent continua (from a mesoscopic viewpoint), as exemplified by an individual crystal. Perhaps we'd better call such a crystal a near continuum.
A crystal can be considered as an intrinsic whole. As a continuum it does not have actual internal boundaries (or, it has them only weakly expressed, like planes of possible cleavage), so it has only potential parts, not actual parts.
Mereotopology, consequently, can recognize crystals (representing continua) as such, and can distinguish them from contigua, as (from) a second type of subsistent entity :
A multitude of individual crystals can form a more or less ordered contiguum, for instance windowpane frost, "beautiful patterns of frost, that rival the most delicate plumes and outdo the finest lace of hand or loom" (BENTLEY & HUMPHREYS, 1962, Snow Crystals, p. 20) (It could be that each 'plume' of a windowpane frost pattern is actually crystallographically continuous, resulting in such a (single) plume to be one crystal).
But such a frost is ordered (patterned) mainly by extrinsic causes. Its order is not precisely repeatable.
In other cases a multitude of crystals can form just an unordered jumble of individual crystals, cemented together, forming no apparent pattern whatsoever, like we see in the case of a granite pebble (See Figure 3). Also in this case the arrangement of the crystals has extrinsic causes.
Mereotopology can distinguish contigua from continua, but it cannot distinguish between an ordered and unordered contiguum.
The next type of discrete mesoscopic entities are individual organisms.
Unicellular organisms consist of discrete cell organelles, and multicellular organisms consist of contiguous cells, making up their body. So it seems evident that at least the multicellular organisms can be considered as contigua. They are ordered (organized) contigua, and this ordering (patterning) has intrinsic causes.
Mereotopology can recognize (multicellular) organisms as contigua, but cannot distinguish them from the other contigua, because it cannot distinguish between "intrinsically caused" and "extrinsically caused". It even cannot distinguish between ordered and unordered contigua.
"intrinsic", "extrinsic", "ordered", "unordered" and "caused" are not purely mereotopological concepts (at least not within the mereotopological framework laid down by SMITH, 1997).
A last type of mesoscopic discrete subsistent entities are artefacts.
Artefacts, like tables, airplanes and bureau lamps, are ordered (patterned) contigua, but the cause of their orderliness is extrinsic. They do not self-assembly.
Mereotopology can distinguish artefacts as more or less tight contigua from scattered wholes, and also from continua like crystals, but it cannot distinguish them from other ordered or unordered contigua.
Because mereotopology not only recognizes crystals and organisms as Substances, but also artefacts and other extrinsic contigua (if they possess an outer boundary, like a granite pebble has one), it employs the concept of Substance in a much broader sense than classical metaphysics (like we see for instance in the writings of Aristotle and of St Thomas Aquinas) does (See the Essays in the Classical Series of this website), and, especially, as seen in the approach we follow within the rest of this website, using the dynamical systems approach (See the Essays of the Non-classical Series of this website).
In order to express this broader sense of the concept we propose to use the term "Mereo-totality", while letting the term "Substance" serve to signify the genuine Substances only : intrinsically organized wholes.
The term "Mereo-totality" accordingly includes genuine Substances, it is true, but not exclusively genuine Substances.
It excludes, however, scattered wholes (genuine aggregates).
So the term "Mereo-totality" signifies either a (near) continuum, or a tight, intrinsically organized contiguum, or a more or less tight, extrinsically organized (or not at all organized) contiguum. In fact, the term "Mereo-totality" just stands for "thing" in the everyday sense.
To be a Mereo-totality, accordingly, is one of the conditions for something to be a genuine Substance, but it is not a sufficient condition : many Mereo-totalities will turn out not to be genuine Substances, as soon as we examine them further, using the dynamical systems approach.
However, because, as we shall see, (mesoscopic) Mereo-totalities can be exactly defined, they constitute real objects, i.e. objective (in contrast with subjective) things, nonetheless. And this is the reason why we will introduce Mereotopology (as developed by the authors mentioned) into this website, as a supplementary approach, in order to understand the concept of Substance more fully.
Until now we spoke about subsistent entities. But these do not come alone. They come with Accidents, i.e. they are represented directly by Determinations. Accidents are not subsistent entities. More specifically, Accidents are temporary determinations of a Substance. While Substances are continuants (they remain what they are, despite accidental changes), Accidents are occurrent entities (SMITH, 1997). Accidents and Substances are linked to each other not as parts to wholes but through the special relation of inherence. So the relation of an Accident to its Substance is not itself a mereotopological relation, but a special kind of dependence relation, linking two realms -- Substances and Accidents -- together. So a (mere) mereotopological interpretation of Reality must at least mention the non-mereotopological relation of inherence between Substance and Accident, if it wants to appreciate and express the division between continuants and occurrent entities.
Accordingly, mereotopology not only focuses on the various types of constituents of Substances, but on those of Accidents too, often in terms of constituents analogous to those found in the realm of Substances. A Mereo-totality is determined by a certain complete set of Accidents. Individual Accidents are not parts of the Mereo-totality, but are occurrent entities and thus having temporal parts. The individual Accidents are not parts of the Mereo-totality in which they inhere, because they are not transportable from one Mereo-totality to another. This, in turn, because an Accident cannot be detached from its Mereo-totality, i.e. from its carrier. It depends for its existence on that carrier.
An Accident is either non-relational or relational (SMITH, 1997).
An Accident is non-relational if it inheres in a single Mereo-totality, like a piece of iron being magnetic, or me having a headache. Such an individual Accident depends on the Mereo-totality in which it is inherent, and thereby forming a complex 'molecular' whole of greater or lesser duration : the concrete Mereo-totality.
An Accident is relational if it depends upon a plurality of Mereo-totalities and thereby joins the latter together into a (more) complex 'molecular' whole of greater or lesser duration : a temporary Mereo-totality cluster, where the glue is represented by the connecting Accident. So in the mereotopological approach we accept entities, like John-and-Mary who are connected with each other by their act of kissing, while in classical metaphysics along the lines of Aristotle and St Thomas -- and also in its updated version based on the dynamical systems approach -- we concentrate either on John (who happens to kiss Mary), or on Mary (who happens to be kissed by John). The question whether it is really necessary to accept entities like "John-and-Mary", or "John-is-kissing-Mary", I will not now decide upon. Important is, however, that Accidents are not parts of their Mereo-totalities. If they were, then relational Accidents could not be real, because one and the same individual entity cannot be a(n) (individual) part of two discrete individual entities (like John and Mary) at the same time.
In the mereotopological approach the notion of "individuum" (an individual) is taken in a much broader sense than in our dynamical systems approach (and also in classical metaphysics as conceived by Aristotle and St Thomas) : To be an individual, a this, is "roughly speaking, to be a full and genuine, one-off, part of the constantly changing order of Nature." (SMITH,1997). We could summarize this view by : An individual is equivalent to individual.
Non-individuals are such as vulpinity or redness, they are entities capable of being exemplified by or realized in a multiplicity of individuals at different places and times (SMITH, 1997). So a mereotopologically conceived individual does not necessarily precisely coincide with a Totality, or Mereo-totality for that matter. "This redness" accordingly is an individual in the mereotopological sense. In the sense of most other approaches it is only individual.
( See the Essays on Individuality :
The Principle of Individuation
What is an Individuum? Part I
What is an Individuum? Part II
What is an Individuum? Part III )
Further we shall, with SMITH, 1997, set that Mereo-totalities (including Substances) in the strict sense (i.e. as bearers of Accidents), and also Accidents, are, within the present approach, considered as in some respect homogeneous entities, which we (again with SMITH) call 'atoms'. These atoms can combine to form 'molecules'.
Another class of non-subsisting entities are "essential parts" (SMITH, 1997).
Subsistent entities and also their non-subsisting Accidents, cannot exist -- cannot be what they specifically are -- unless certain parts of them exist : their essential parts. So Jim cannot exist as such, unless (his) humanity (his human nature) exists. But, as is evident from the example, essential parts are not concrete parts : Sodium ions and Chlorine ions -- an ion is an electrically charged atom -- are necessary parts with respect to the constitution of a Salt crystal, but the identity (whatness) of that Salt crystal is not dependent on these particular Sodium and Chlorine ions here-and-now present in the crystal.
So essential parts are not subsistent entities.
In fact the notion of "essential parts" is not properly belonging to mereotopology, but must be dealt with by a Substance-Accident metaphysics.
A final class of non-subsistent entities are universals. But as we shall argue, universals, as universals, do not exist as real entities at all, but only as linguistic or logical entities : They, as universals, are terms, universal terms, signifying several real entities univocally.
The item to be defined will be connected to the definition by the sign " = ", which means : " if and only if ". The Definiendum ( = item to be defined ) is placed between brackets (...), so also the Definiens ( = the definition).
Definition 1
( X is disjoint from Y ) = ( X and Y have no parts in common )
Definition 2
(X is discrete from Y ) = ( X and Y are individuals which have no individual parts in common )
This redness of this stone, and that magnetizability of that piece of iron, are discrete, but they are also disjoint. They do not have any part whatsoever in common, which means that they do not have even universal parts in common except with respect to the highest universals, in this case Quality. This redness and that magnetizability are both qualities, it is true, but Quality, as a highest genus, is just a particular way of being, it is not a part. If there is a universal, that, with respect to the degree of generality, lies between redness and magnetizability on the one hand, and Quality on the other, then this redness and that magnetizability are not fully disjoint. So to be disjoint from each other can come in several degrees.
This magnetizability and this length of 1.50 centimeter are (more) strongly disjoint, because they belong to totally different categories (genera) of Being (respectively to Quality and to Quantity).
This Salt crystal and that Salt crystal are both individuals, and although they do have an essential part in common, namely their chemical composition, NaCl, they do not have individual parts in common, so they are discrete from each other.
In order to understand the relation between a Substance and its Accidents we must work out the notion of inherence. To capture at least part of what is involved in that notion we need the notion of specific dependence (SMITH, 1997) :
Definition 3
( X is specifically dependent on Y ) = ( [1] X is discrete from Y, and [2] X is necessarily such that it cannot exist unless Y exists. )
A special, and important case is : one-sided specific dependency :
Definition 4
( X is one-sidedly specifically dependent on Y ) = ( [1] X is discrete from Y, and [2] X is necessarily such that it cannot exist unless Y exists, but not vice versa )
Inherence in general is a case of one-sided specific dependence (SMITH leaves open the question whether there are examples of one-sided specific dependence which are not examples of inherence). In fact inherence is not a mereotopological relation : if Y can exist without X, in the sense that it can exist as separated from X, (which is then a mereotopological relation), then X can exist without Y, in the sense that it can exist as separated from Y. And this fails to meet the condition of inherence, so the inherence relation bears no relevance to any 'separation thought experiment'. That's why indeed an Accident is not a part. So mereotopology cannot cover the Mereototality-Accident relation all by itself. We need concepts that lie outside the domain of mereotopology.
In some respects the converse of specific dependence is the relation separability :
Definition 5
( X and Y are mutually separable ) = ( [1] X is not necesarily such that any part of Y exists, and [2] Y is not necessarily such that any part of X exists. )
For example a pair of stones X and Y, is mutually separable.
Definition 6
( X is a one-sidedly separable part of Y ) = ( [1] X is a proper part of Y, [2] some part of Y discrete from X is specifically dependent on X, [3] X is not specifically dependent on any part of Y discrete from X. )
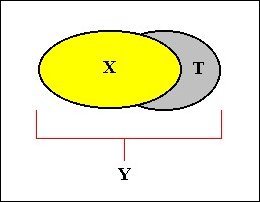
SMITH gives the following example : X is a human being, and Y is the sum of X together with some one of X's thought.
Let us denote "some part of Y discrete from X, that is specifically dependent on X" as T.
Then in this definition, [2] implies that T cannot be separated from X, and [3] implies that X can exist, separated from T. (See figure 1)
An individual human being X can exist separated from a thought T (he can have thought R instead), but that thought T cannot exist separately from that human being, or from any human being whatsoever. But in this example "separated" should not mean the result of an (actually executed) division, in this case a division of X + T into X and T, because X and T are not parts of X + T. The human being X cannot be separated from his thought T, neither can T be separated from the human being X. Or, in other words, while X is thinking T, he cannot be separated from T. When X is thinking T, T is not a part of Y, but a condition, or state, in which X finds itself : T is an Accident of X. And because T is just a condition (Accident) of X, T does not involve any boundary dependence (See below) in relation to X, and therefore X is not an actual or potential part (and consequently not a one-sidedly separable part) of Y. So it seems to me that Definition 6 (given as such by SMITH, 1997) contains an inconsistency, by associating part with specific dependence, which in this context implies inherence. And on the second page (as SMITH' article is presented on the Internet) SMITH states:
"Accidents and substances will then be linked not as parts to wholes, but through the special relation of inherence." And on p. 5 he says :
"Note that the relation of boundary dependence [See Definition 10] does not hold between an accident and its substantial carrier." ( The human being X is the carrier of his thought T ). This means that there is no boundary between X and T.
Despite the detected mutual inseparability of X and T, there must be some sort of asymmetry involved. Let us look for this asymmetry.
T is a here-and-now condition of X (We can interpret every Accident as a condition of its carrier).
Because T is a condition, T implies something of which it is a condition. This "something" could be any of the possible carriers of T, not necessarily X.
But the same holds for X :
X always implies a condition in which it should find itself. This condition could be any of the possible conditions, it needs not necessarily to be T.
We still haven't found the asymmetry, although "carrier" and "carried" seem to point to one.
To reveal the asymmetry, we need to involve the time dimension, and for this a dynamical systems approach seems to be appropriate.
In such an approach T is (a part of) a system state. At the next moment T is replaced by, say, T '. The whole succession of states, or, already a part of it, is equivalent to the dynamical system. This system itself can be considered to stay the same. Why? Because its dynamical law, governing this succession, can be considered to stay the same.
Some states of such a system could be partially determined by extrinsic causes. They are then perturbations of the system. But the next state that should appear after the perturbation is nonetheless determined by the same dynamical law, unless that law itself has changed as an effect of that perturbation (More details of this state of affairs can be found in the Essays of the Non-classical Series of this website. I shall not dwell on them here).
We've finally found the asymmetry : The system (represented by its dynamical law) stays the same, while its different states succeed one another.
So the phenomenon of inherence, for example the inherence of the thought T in a human being X, is much more subtle than something like " X, that is a one-sidedly separable part of Y, meaning that X is separable from T, but T is not separable from X ".
[1] of Definition 6 reads that X is a proper part of Y. This implies that T ( which is discrete from X ) is also a proper part of Y (also implied by [2]). But X and T should be conceived on different ontological levels. We cannot just add them arithmetically together, and say " X + T = Y ". Only if accompanied by the admittance of the ontologically non-equivalence of X and T, we can say " X + T = Y ".
I shall elaborate on this further, in the sequel.
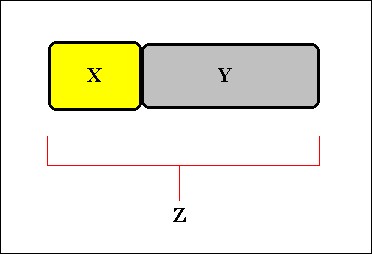
Definition 7
( X and Y form a partition of Z ) = ( [1] X and Y are parts of Z, [2] X and Y are discrete from each other, [3] no part of Z is discrete from both X and Y. )
A partition of Z into X and Y results in Z being a tight contiguum, consisting solely of X and Y. There is no common boundary between X and Y (See figure 2 ).
Definition 8
( X is atomic ) = ( [1] X is an individual, [2] X does not involve inherence, [3] there is no partition of X into mutually separable parts. )
For [2] SMITH sets : X has no one-sidedly separable parts. I have replaced this by : X does not involve inherence. This I have done to eliminate the incompatibility between part and specific dependence. A Mereo-totality (and also a Totality, a genuine Substance) can be what it is, and remain what it was, without this particular Accident A, it can have instead Accident A' from the same category (it can be blue instead of red, but it must have some color). So we can distinguish this Mereo-totality from those Accidents A and A' (and from all Accidents of that category for that matter) all together. When we apply this to all accidental categories, then we have the Mereo-totality proper. It is thereby not actually separated from its Accidents, but considered without those Accidents. We can do so, because a Mereo-totality is only generically dependent on its Accidents, i.e. it must bear a certain complete set of Accidents, but the members of this set do not need to be fixed once and for all. A Mereo-totality (and consequently also a genuine Substance) so conceived, i.e. as the carrier-only (carrier of Accidents), does indeed not involve any inherence relation (anymore).
In order to avoid misconceptions, let us state this more precisely : A Mereo-totality can never be (i.e. exist) without Accidents. These are always co-signified by the term "Mereo-totality" or by the term "Substance", but this co-signification is only implicit. When these terms are used in the explicit sense of "the carrier-only", then they, in their signification, explicitly leave out the Accidents. Later we will elaborate on this issue further.
Also an Accident can be considered (not be) without the Substance in which it inheres. However, because of a different reason, namely by (the possibility of) transforming it into a universal, like for instance redness.
Redness can be 'applied' to, i.e. instantiated by, many individual Mereo-totalities, each of those individuates redness. Hence "redness" is also just generically dependent on its carrier. So we can conceive of this redness (i.e. the "red" of this red thing) 'before' instantiation, and then we get redness. Redness so conceived, i.e. as an abstract term, does not involve any relation of inherence. By the term "red", a concrete term, this relation is co-signified, but only implicitly so, while the term "red thing" co-signifies this relation explicitly.
For [3], "there is no partition of X into mutually separable parts", we can say the following : [3] is ruling out aggregates, also tight contigua. It accordingly narrows the range of enities that can legitimately be called Mereo-totalities. On the first page of SMITH' article (1997) SMITH referred to human beings, oxen, logs of wood, icebergs, and planets as individual Substances. But icebergs and planets certainly display partitions into mutually separable parts. We can separate many parts from them without thereby involving common boundaries. So such things fail to be atomic, and therefore to be Mereo-totalities (and by consequence they fail to be Substances). All this because of not satisfying [3], not because they turn out to be only substantial -- See below -- (they aren't substantial either), but because they are aggregates.
But some types of aggregate (aggregates according to the dynamical systems approach) are such as to be recognized by mereotopology not as aggregates but still as Mereo-totalities, as we will see shortly.
But [3] of Definition 8 says more :
If we allow things like granite pebbles, and artefacts like tables and spaceships, and, especially multicellular organisms (which should be interpreted as (tight) contigua), as Mereo-totalities, then we admit such a Mereo-totality to possess a partition into mutually separable parts. And admitting them to be Mereo-totalities (and some of them even Substances) implies that they should be atomic (See Definitions 12 and 9), but then they contradict [3] of Definition 8.
Being atomic, such Mereo-totalities should be without such partitions. This means, that if we nonetheless consider them (with good reasons) to be Mereo-totalities, then Definition 12 must represent them as the carriers-only (of their Accidents), if we could prove that all such partitions are just accidental determinations. But it could also turn out that at least multicellular organisms are continuous, and thus having no such partitions. We shall return to these matters shortly.
Definition 9
( X is substantial ) = ( [1] X is atomic and [2] X is not specifically dependent on any other entity. )
If we now consider Darius' arm, still attached to his body, this arm satisfies being substantial, because it satisfies being atomic and is not specifically dependent on any other entity. It does not need any ontological bearer. It is atomic because it is not an aggregate in the mereotopological sense, because any attemted partition (any cut through this arm) involves common boundaries. Such a boundary is an individual part, and this individual part is a common part and so the parts resulting from the attempted partition are not discrete, and consequently they are not mutually separable (because, again, they have a common boundary, and such a boundary is dependent for its existence on both parts). So [3] of Definition 8 is satisfied. And because the arm is individual, and (if abstractly considered, i.e. considered as the carrier-(of Accidents)-only) does not involve inherence (NOTE 1), [1] and [2] of definition 8 are also satisfied. And because the arm satisfies [2] of Definition 9, the still-attached arm of Darius is substantial, i.e. it is a part of a Mereo-totality (and moreover of a genuine Substance). It is in short a substantial part. It is a part of the carrier-only.
But on actual separation of the arm from Darius' body the arm is not a part anymore and will have a complete boundary of its own. It has become mereotopologically independent, it is a Mereo-totality, i.e. a Substance (in its own right) in the mereotopological sense. But when we supplement this mereotopological treatment with considerations from the dynamical systems approach, then the detached arm is only a Mereo-totality, it is not a genuine Totality, and equivalently, not a genuine Substance within that supplemented approach.
Definition 10
( X is boundary dependent on Y ) = ( [1] X is a proper individual part of Y, and [2] X is necessarily such that either Y exists or there exists some part of Y properly including X, and [3] each individual part of X satisfies [2]. )
For example : X is the surface of an apple, and Y is the apple itself. With "surface" we do not here mean the skin or rind of the object, but the surface in a geometric sense. This surface is boundary dependent. It is a genuine mereotopological relation.
Definition 11
( X is a boundary ) = ( X is boundary dependent on some individual )
A boundary can be :
[ In fact Socrates' arm does correspond to a physical discontinuity, namely the joint between the relevant bones. It is clear therefore, that a Substance, like Socrates, is -- in the present discussion -- considered at a high level, which means that Socrates has, it is true, a definite outer morphology, but is considered to be a homogenous entity (This is allowed because his Essence pervades his whole body uniformly). ]
The boundary in this case yields a partition of the Mereo-totality into substantials (i.e. potential parts of a Mereo-totality, and, by implication of a Substance), as do also all arbitrary inner boundaries. When we examine a certain uni-cellular organism, we see that it has an outer boundary, represented by the cell-membrane, so this boundary is a bona fide boundary, but, on closer inspection it turns out not completely to be so. It has pores, but these pores still define a boundary (running across the aperture of the pore) although this boundary is not represented by a physical discontinuity. So it is a fiat boundary. But although it is a fiat boundary, it is not arbitrary.

The outer boundary of the Solar system is intrinsic (The Solar system is (the product of) a dynamical system, and this system defines (from within) the outer boundary. By implication of the nature of this system and its operating forces this boundary is not sharp, but is nonetheless a genuine boundary). This boundary is then by implication non-arbitrary. It is however a fiat boundary, because it is not represented by a clear physical discontinuity, but nevertheless relates to objective features within the system.
The outer boundary of the state of Colorado is an arbitrary boundary, and by consequence extrinsic. It is not a fiat boundary, because, although this boundary is not represented by a physical discontinuity, it does not relate to any objective feature of the terrain itself.
( X is a Mereo-totality ) = ( [1] X is substantial, [2] X has a boundary, [3] there is no Y that is boundary dependent on X and on some individual that has parts discrete from X. )
[3] excludes substantial parts, i.e. it excludes the possibility that a substantial part is itself a Mereo-totality (and by implication a Substance).
If there were some Y that is boundary dependent on X and at the same time boundary dependent on some individual that has parts discrete from X, then X would be connected with something (by means of Y) that itself extends spatially beyond X, and so X would be just a substantial part of a larger whole comprising X and more. See Figure 4.
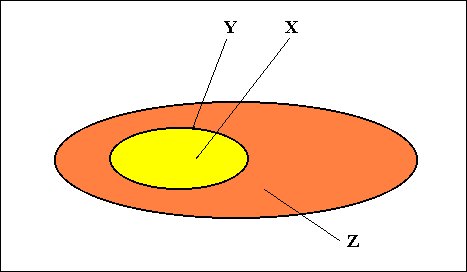
So a Mereo-totality X (and consequently not X in the situation depicted by Figure 4) can have parts, but these parts are not Mereo-totalities themselves, they are immediately adjacent to each other, i.e. the spaces between these parts also belong to the Mereo-totality, implying that they also are parts. So the partition effected by these parts does not admit that there is some 'part' P of X that is discrete from all the (genuine) parts of X.
P must itself be a genuine part of X.
And now P is not discrete from all parts of X, because, although it could be discrete from some parts of X, there is now at least one part of X from which it is not discrete, namely itself. This is demanded by the definition of "atomic", because if there were entities between the parts that do not belong to the object, then "mutually separable parts" is not beforehand excluded. They could be separated (by some separating action), or are even already separated, namely by such entities not belonging to the object and (these entities together) surrounding the parts :
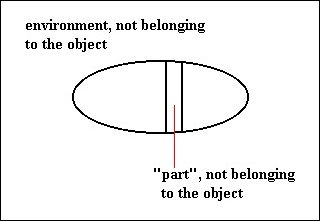
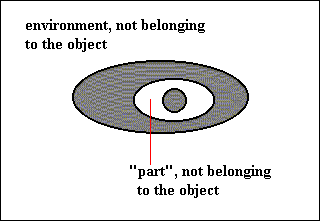
Figure 5b. Another instance of two entities : An environment and a 'part' not belonging to the object.
Besides genuine substantial parts, we must now speak about another type of part, namely, partially or wholly contiguous parts ( which seems to be excluded by Definition 8 ).
Consider Figure 6 :
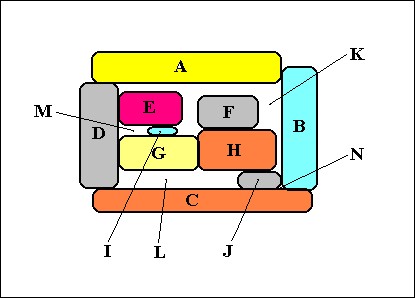
Multicellular organismic bodies seem to be contigua (genuine or not genuine). Each cell of such a body seems to have its own (physical) boundary, which is especially prominent in the case of plants.
We can compare such an organism mereotopologically with Figure 6. If some of K, L, M and N, say, K, from that Figure, do not belong to the object figured, then the object that remains is no longer X, but, say Y.
Y is then surrounding K, and K can be considered to be a cavity inside Y. This cavity is not a part of Y, but it still is a part of X.
X is just the mereological sum of A, B, C, D, E, F, G, H, I, J, K, L, M and N. And K is a part of this mereological sum. We must investigate such a contiguum further, in order to assess the ontological status of multicellular organisms.
Definition 12 rules out substantial parts, in the sense that such a part is itself not a Mereo-totality. But what about the entities A, B, C, etc. depicted in figure 6 ? Are they Mereo-totalities themselves? Or is X a Mereototality, or Y?
SMITH, 1997, tries to answer this, using the concept of boundary dependence. If the boundaries between A, B, C, etc. are not boundary dependent on both entities which are separated by these boundaries, then each entity A, B, C, etc. is itself a Mereo-totality or Substance, even when those boundaries are, in a way, common boundaries (where there is genuine contact).
SMITH argues this with the example of two billiard balls which are in contact with each other, as depicted in Figure 7 :
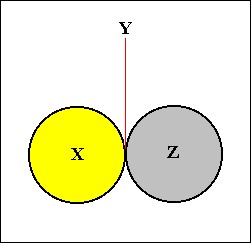
Let us now assess the status of one billiard ball, say, X. The boundary, Y, between the two billiard balls, that is, between X and Z, is not boundary dependent on both X and Z, i.e. it is not boundary dependent on X + Z, because this boundary still exists when we destroy one of the balls. So X does satisfy [3] of Definition 12. Moreover X is substantial, and X has a boundary, so X satisfies Definition 12. This implies that X is a Mereo-totality, also when X is in contact with another ball.
Let us now assess the status of the complex of the two-balls-in-contact, that is, X + Z.
This complex does not possess a boundary or piece of boundary that is boundary dependent both on X + Z and on some W that has parts discrete from X + Z. This is because the boundary of X + Z remains when W is removed or destroyed. So X + Z satisfies [3] of Definition 12. And because X + Z is substantial and has a boundary, it follows that X + Z is a Mereo-totality, or even a Substance. Because X is itself a Substance, and Z is itself a Substance, it follows that a Substance can consist of parts which are themselves Substances, which contradicts a conclusion of SMITH.
But wait a minute.
We asserted that X + Z was substantial. Then it must be atomic (Definition 9.). Let us now recall the Definition of atomic :
Definition 8
( X is atomic ) = ( [1] X is an individual, [2] X does not involve inherence, [3] there is no partition of X into mutually separable parts. )
The complex of the two billiard balls, i.e. the complex X + Z, is clearly partitioned into X and Z. Let us recall the definition of partition, and substituting some of its symbols, to make it easy to read with respect to our example :
Definition 7
( X and Z form a partition of X + Z ) = ( [1] X and Z are parts of X + Z, [2] X and Z are discrete from each other, [3] no part of X + Z is discrete from both X and Z. )
Applied to our example :
X and Z are indeed parts of X + Z ([1] is satisfied), X and Z are indeed discrete from each other, they have no individual parts in common ([2] is satisfied), no part of X + Z is indeed discrete from both X and Z ([3] is satisfied). So X and Z form indeed a partition of X + Z.
Because the parts X and Z are mutually separable, they indeed form a partition of X + Z into mutual separable parts. So [3] of Definition 8 is violated, implying that X + Z is not atomic. And thus X + Z is not substantial, implying further that [1] of Definition 12 is violated, so X + Z is not a Mereo-totality, and by implication, not a Substance.
So it is already [3] from Definition 8 which decides that the complex of the two contiguous billiard balls is not a Substance.
So a whole, consisting of contiguous parts would not be a Substance, according to SMITH' definitions.
But this could, according to me, imply that multicellular organisms are not Substances. So if we nonetheless admit them to be Substances, because they seem to be even the primary instances of Substance, then mereotopology alone cannot decide this. This is to be expected because the relation "belongs to", in the sense that some entity belongs to some other entity, is not a purely mereotopological concept. We must stipulate that the interstices between organic tissue cells belong to the organism. So these interstices are then themselves also parts of that organism. And then the boundary between the boundary of a cell and the interstice (dividing it from another cell) could, it is true, still be interpreted as a bona fide boundary, but this boundary is boundary dependent towards both sides, implying that each cell is not separable from the interstice, and vice versa, so condition [3] of Definition 8 is satisfied, and then each cell becomes indeed just a substantial part of the organism. It also implies that an organism is not a contiguum but a, albeit heterogeneous, continuum [It is a continuum in the sense that, starting from one point (location) within the entity, we can reach every other point of that entity, without ever having (temporarily) to leave the confines of that entity. So it is a continuum by way of 'belonging to', that is, it is (only) a metaphysical continuum. It is not a mathematical continuum, because it has actual parts (if the latter indeed allow themselves to be interpreted as parts)].
In other cases we must stipulate that some cavities do not belong to the organism, by means of a functional argument, i.e. not by means of a mereotopological argument.
We can detect this clearly in the discussion of SMITH & BROGAARD, 2000, p. 25, where they discuss the question whether some items like the amnionic cavity, or the digestive canal, do or do not belong to the organism in question.
Definition 12, while basing itself on the Definitions 8, 9, 10 and 11, pretends to define a Mereo-totality (and by implication, a genuine Substance).
We should, however, investigate what then precisely is being defined. Is it the (Mereo-totality insofar as it is the) carrier-only, or is it the full-fledged Mereo-totality? And if (it defines just) the carrier-only, what then is the nature of such a carrier-only? Is it contiguous or continuous, and if the latter, is it homogeneous or heterogeneous?
In order for an entity X to be a Mereo-totality Definition 12 demands X to be substantial, and that means, according to Definition 9, that X must be atomic and not specifically dependent on any other entity. So X is the substantial part of the Substance-Accident composite, which means that X (as finally defined in Definition 12) should be the carrier-only (A substance-accident composite is not atomic) ( The mereototality-as-carrier-only is only generically dependent on its accidents).
This carrier-only (X) should then have the following three important characteristics :
(1). There is no partition of X into mutually separable parts (Definition 8). This means that the carrier-only must be a complete unity, and this in turn means that it is not a contiguum (like the two billiard balls), even not a tight contiguum (See the next Figure).

Figure 8.
(1). Contiguum (2). Tight Contiguum
A partition of non-separable parts is admitted though.
(2). X does not involve inherence (Definition 8).
(3). X is not a substantial part (Definition 12), i.e. it is not a proper part of a carrier-only.
As we see -- in (2) -- a carrier-only, insofar as carrier-only, does not involve entities that are one-sidedly specifically dependent on it (Definition 4). Such entities (Accidents) are conceptually removed (from a full-fledged Mereo-totality) resulting in the carrier-only.
What exactly is (conceptually) removed?
Well, only those entities that are removable at all, i.e. they should be removable without destroying the specific identity of the Mereo-totality. If we would remove all determinations whatsoever, then we would end up with just Prime Matter, the ultimate carrier. But according to Definition 12 X should have at least a boundary (which is already a determination ), so X cannot figure in that Definition as just Prime Matter.
The only entities that are (conceptually) removable, without destroying the specific identity of the Mereo-totality, are the occurrent entities, i.e. the replaceable determinations (Accidents), like being tanned by the summer sun.
So after the removal of such entities we should be left with the carrier-only. And this carrier-only will still possess several determinations, namely the ones that cannot be removed. These are determinations -- or sequences of them, each sequence consisting of a series of successive determinations, which (sequences) are then each for themselves (interpretable as) single determinations – that are directly caused by the Essence of the Mereo-totality. They are consequently not just compulsorily presupposed types of determination, which are (also) not removable, but are completely specified individual determinations that are necessary for the (content of the) Mereo-totality's specific identity. They are essential parts, essential structures, of the Mereo-totality. They cannot be just potential or virtual.
This needs some further elaborations :
In the dynamical systems approach a necessary sequence of successive determinations (of an individual Mereo-totality) represents a necessary series of successive system states. Such a sequence is therefore a direct effect of the dynamical law (= the Essence of the Mereo-totality), and indeed as such is an essential part (discussed further down) of the Mereo-totality (which should in this context be a genuine Substance). But each individual determination (as a member) of such a successive series will eventually and necessarily be replaced by another determination, namely by the next one in that successive series. And then by the next one, etc., according to the dynamical law.
So only the series-as-a-whole is not replaceable, i.e. the same series will appear in other individuals of the same species, while its members -- the individual determinations making up the series -- are (replaceable).
And if a determination is replaceable in the context of a (full-fledged) Mereo-totality, then it is removable in the context of (obtaining) a carrier-only. Thereby it should be understood that a replacement of a determination is a physical operation, while a removal of such a determination is only a conceptual operation, in order to obtain (i.e. isolate) the carrier-only.
So now we can better assess which determinations are removable (in order to conceptually obtain the carrier-only), and which are not :
(1). Necessary determinations, that are constantly present – i.e. persistent – in the Mereo-totality, are not replaceable, and consequently not removable. When such a determination would nonetheless be removed, or even just replaced by another, the original specific identity of the relevant Mereo-totality is destroyed.
(2). Per accidens determinations are triggered by extrinsic agents. Such a determination can be replaced by another, without destroying the specific identity of the Mereo-totality, and consequently it can be (conceptually) removed.
(3). Determinations, that are members of necessary successive sequences, are replaceable only in a certain restricted sense. Such a determination can indeed be replaced by another, without destroying the specific identity of the Mereo-totality, provided it will be replaced by the next member of the particular necessary successive series of determinations. And because it can be (so) physically replaced, it can conceptually be removed (in order to isolate the carrier-only).
The determinations of (1) are strongly implied by the Essence of the Mereo-totality. They are in fact not determinations of a substrate, but the substrate itself -- albeit not the ultimate substrate -- i.e. they are the substrate for the other determinations. This can be expressed by calling them essential determinations (or essential parts). They belong (already) to the carrier-only, because they cannot be removed.
The determinations of (2) are not at all implied by the Essence of the Mereo-totality. Such a determination can be physically replaced by virtually any determination from the same (Aristotelian) category. Therefore it can conceptually be removed, and consequently does not belong to the carrier-only.
The determinations of (3) stand more or less in between : as successive sequences they are essential parts, and (already) belong to the carrier-only, while each individual member of such a sequence is – albeit in a restricted sense – physically replaceable, and thus conceptually removable, and consequently not (already) belonging to the carrier-only.
It is important to realize that for a full-fledged Mereo-totality no determination can be removed just like that. It can only be replaced by another determination belonging to the same (Aristotelian) category. When we speak of really removing a determination, we leave the domain of a full-fledged Mereo-totality (from which that determination is supposed to be removed), and enter that of a carrier-only. Such a removal indeed destroys the full-fledged Mereo-totality (because it is then not full-fledged anymore) and leads to the intended isolation of the carrier-only. The removal is in this case a just conceptual operation (while a replacement is a physical operation).
For the full-fledged Mereo-totality to actually be able to exist it must involve a complete set of types of determinations, intrinsic and extrinsic.
If that Mereo-totality is viewed over the whole time span of its existence, then not all determinations, implied by this set, need to be completely specified (For example, Socrates' length is not a once and for all fixed quantity, it varies during his life time). But some of them, namely the essential determinations, should be so specified.
If, on the other hand, that (same) Mereo-totality is viewed as a here-and-now entity, then all determinations, implied by the above mentioned set of types, must be completely specified (For example, with respect to a quality : it should not be specified as just (a) COLOR, but (specified) as, say, (a particular nuance of) RED). In general, the Mereo-totality should be at a definite space-time location, it should have definite quantities, qualities and relations.
A non-completely specified, general, determination can at one point in time become specified (actualized) as (being determination) A, and at another point in time become specified as (being determination) B, while the specific identity of the Mereo-totality remains the same, and with it its essental parts (which are caused by, or derived from, that identity (Essence)) (Later we will expound that the difference between the essential parts on the one hand, and the Essence on the other, boils down to a difference of (ontological) domain : The essential parts are phenotypical expressions of the Essence which itself resides in the genotypical domain of the Mereo-totality).
These essential parts will surely involve partitions.
When we stipulate that the interstices that are involved in such partitions intrinsically b e l o n g to the Mereo-totality, and thus converting them into partitions into non-separable parts, the Mereo-totality is then a (albeit heterogeneous) continuum, because the parts, resulting in virtue of such a partition, are then only substantial parts (they are not themselves Mereo-totalities or Substances), but are nevertheless actual (also their boundaries are actual). The mereo-totality is then a 'belonging to' continuum, that is, a metaphysical continuum, and not a mathematical continuum (If, however, the pattern of interstices and parts allow themselves to be interpreted as just replaceable determinations of the Totality [and nothing more, that is, they are then not parts], then we have a heterogeneous continuum).
If the Mereo-totality is now viewed (only) insofar as it is the carrier-only , then all occurrent entities (i.e. all Accidents) are (conceptually) removed. This means that the carrier-only cannot be viewed as a here-and-now entity (because, among other things, a definite point in time – the answer to the question when the Mereo-totality is – has been (conceptually) removed), and this in turn means that in the carrier-only only the essential determinations are completely specified, and thus actual. All other determinations (namely all replaceable determinations, i.e. Accidents) are only potentially present.
Further, the above (mentioned) stipulation about the status of the interstices of the Mereo-totality, implies that also the carrier-only of such a Mereo-totality is a (heterogeneous) continuum. It is always heterogeneous : If the interstices and parts are interpreted as actual parts (which is compatible with (just) a 'belonging to' continuum), the continuum is heterogeneous. If, on the other hand, they are interpreted as (just) virtual parts, then they are actual determinations (accidents), and the continuum is still heterogeneous.
So far so good, but what then is the difference between, on the one hand, the carrier-only, and, on the other hand, the corresponding Mereo-totality considered over the whole time span of its existence , i.e. the historical (individual) Mereo-totality?
Well, there is no difference.
The historical Mereo-totality IS the carrier-only.
The Mereo-totality is a totality of its determinations. Some of them are necessary determinations, others are replaceable determinations. The dynamics of the replacement of one Accident by another implies a substrate. This substrate is the whole Mereo-totality minus the Accidents actually involved in that (particular) dynamics, and this substrate is the carrier-only. It is the carrier-only with respect to those particular Accidents actually involved in that dynamics of replacement. The carrier-only, so conceived, does not involve inherence with respect to those particular Accidents, but it does involve inherence with respect to all the remaining Accidents.
And when we now consider all replaceable determinations (Accidents) 'simultaneously' involved in such a dynamics of replacement, we finally have (conceptually arrived at) the (genuine) carrier-only just like that, after we have removed those determinations.
This carrier-only is the result of the (conceptual) exclusion of all occurrent entities. However, as has been said, each necessary successive sequence of determinations, seen as a whole, is not excluded. They are, together with the intrinsically constant determinations, considered as essential determinations, because successive replacement is (ex hypothesi) a necessary pattern.
And in this way we obtain the 'Substance' as it was understood already for a
long time : That which lies under the replaceable determinations.
It comprises the Essence, and all entities that are directly and necessarily caused by, or derived from, it, insofar as they are not replaceable.
There are two categories of concrete real things (Mereototalities) :
| MEREO-TOTALITIES (things) | ||
| LOW-DEGREE MEREO-TOTALITIES | HIGH-DEGREE MEREO-TOTALITIES | |
| = DETACHED PARTS OF SUBSTANCES, OR, EXTRINSIC TIGHT CONTIGUA |
= GENUINE SUBSTANCES ( TOTALITIES ) ( INTRINSIC CONTINUA, GENERATED BY ONE DYNAMICAL SYSTEM ) |
|
If an atomic entity is specifically dependent on a whole Mereo-totality or Substance, then this entity is an Accident (See the relevant definitions below). It needs a carrier for it to be able to exist. It is a DEPENDENT ATOM, because it can only co-exist.
Definition 13
( X is an accidental ) = ( [1] X is atomic and [2] X is specifically dependent on some individual Y. )
An accidental could be a determination of only a part of a Mereo-totality (or Substance), and as such it actualizes a potential part of the latter. If we interpret non-essential parts of a Mereototality, and especially of a Substance, as mere regions, i.e. as virtual parts, then an accidental can actualize just a quality in a certain region of the Substance.
Definition 14
( X is an accident of Y ) = ( [1] X is an accidental of Y, [2] Y is a Mereo-totality, [3] there is no substantial proper part Z of Y such that X is an accidental of Z. )
Definition 15
( X is an atom ) = ( X is either a Mereo-totality (or Substance) as carrier-only, or X is an Accident. )
The relation of specific dependence is the bond which holds atoms together in molecules of different sorts. Such molecules are the referents of simple empirical judgments, such as "Socrates is tanned", "John is kissing Mary", etc.
To capture the notion of molecule SMITH defines :
Definition 16
( X is closed under specific dependence ) = ( no part of X is specifically dependent on any entity discrete from X. )
"no part of X" can also mean X itself.
So X can be a Mereo-totality as carrier-only, a Substance as carrier-only (See Remark), or a Mereo-totality (Substance)-Accident composite. It cannot be an accidental, implying that it cannot be an Accident.
Remark : A carrier-only is only generically dependent on its being determined by a (complete) set of types of (replaceable) determinations. Ontologically it does not matter precisely which determination (here, which Accident) represents each type.
Although definition 16 is meant to rule out accidentals, on closer scrutinity it turns out not to do so. An accidental is, just like the carrier-only, not specifically dependent (on a carrier), it is only generically dependent on its having a carrier. Thus something being an accidental is not ruled out by that Definition, as given by SMITH.
If however we hold (with SMITH) that the dependence of Accidents on their carriers (substrates) is specific, i.e. a one-sided specific dependence, then accidentals and Accidents are indeed ruled out by something that is closed under specific dependence. Indeed on p. 4 of the Internet version of his article SMITH states :
"My headache, for example, is specifically dependent on me (as also on my head)."
Of course in this case my headache is not just dependent on one or another (human) substrate, but is dependent on a certain individual, namely me. It is an individual Accident. However, this is because the Accident headache is qualified by "my". But "my" is extrinsic to a headache as such, so it should not be included in a term which purports to signify an Accident.
An Accident needs an appropriate substrate in order to exist, but this still leaves open several possibilities for a substrate, and thus an Accident (and also an accidental) is just generically dependent on a substrate.
Although I will not once and for all rule out the possible asymmetry between, on the one hand, the dependence of a carrier-only (substrate) on Accidents, which is generic, and, on the other hand, the dependence (specific) of an Accident on its carrier, I, for the time being, and preferably, will stick to the generic nature of the dependence of Accidents on their having a carrier, and should change the relevant Definition accordingly.
So I will propose to amend Definition 16, in order to exclude accidentals and consequently Accidents.
The dependence relation between an Accident and its having a carrier is an asymmetric relation in the following way :
The carrier-only is upwardly dependent on its having Accidents (The dependence is a generic one). The Accident is downwardly dependent on its having a carrier (The dependence is also of a generic nature).
So if we want to rule out Accidents we should exclude downward dependence. If we do so then we exclude accidentals and Accidents, but admit Mereototality(Substance)-Accident composites and also carriers-only.
So we define :
Definition 16a
(X is closed under downward dependence) = (no part of X is downwardly dependent on any entity discrete from X)
The next definition (defining a molecule) should rule out carriers-only :
Definition 17
( X is a molecule ) = ( [1] X is closed under downward dependence, [2] X has discrete parts, [3] all atoms Y, Z which are parts of X are connected, directly or indirectly, by relations of specific or generic dependence. )
In [1] we have replaced "specific" in SMITH' definition with "downward".
In [3] we have added "or generic". All those dependencies are meant to be ontological, which means that they are not referring to efficient causality.
[1] rules out Accidents (i.e. it rules out that X is an Accident-only).
[2] rules out that X is a carrier-only ([3] of Definition 8).
So the definition rules out atoms-only.
[3] admits ontological wholes.
So a molecule X is, for example, "John is kissing Mary". John is a part of X, Mary is a part of X. They are moreover discrete parts. But these parts are not downwardly dependent on any entity discrete from X, i.e. discrete from "John is kissing Mary". So [1] of Definition 17 is satisfied at least with respect to the parts John and Mary.
When we consider the Accident "is kissing" also as a part of X (but, see below), then also this part is not downwardly dependent on any entity discrete from X. So X, i.e. "John is kissing Mary", satisfies Definition 16a, and by implication [1] of Definition 17.
[2] of Definition 17 is also satisfied, because John and Mary are discrete parts of X.
John is an atom of X, Mary is an atom of X, and "is kissing" is an atom of X. Moreover John, Mary and "is kissing" are all the atoms of X. These atoms are connected by relations of specific or generic dependence. So [3] of Definition 17 is satisfied. They are, as has been said, not downwardly dependent on any entity discrete from "John is kissing Mary". So "John is kissing Mary" satisfies Definition 17.
An analogous argument applies to (simple molecules like) "Socrates-tanned", "Socrates is running", etc.
If we consider a simple molecule, like Socrates-tanned, then the atom being-tanned is connected with the atom Socrates by a relation of specific (NOTE 2) or generic dependence, but, they cannot be considered as parts, because Substance and Accident are not related to each other as parts to a whole. But above, in connection with a complex molecule, we said that John is a part of X, Mary is a part of X, and also "is kissing" is a part of X. But they cannot be genuine parts either, they are atoms, constituting the molecule X, but not in the way that parts constitute a whole. So John as well as Mary should be interpreted as carriers-only, connected by the dependent atom "is kissing" (not considering all the other Accidents).
"is kissing" inheres in John, and, in the form of "is being kissed" it inheres in Mary. Inherence does not involve parts, which means that no parts are created or connected by it.
So it would according to me be more appropriate when we replace the mereotopological notion of "are parts of " in the definition by the metaphysical notion of "belongs to".
But despite of this, we must distinguish between a simple molecule such as Socrates-tanned and a complex molecule such as John-is-kissing-Mary, because in the latter case we have not one, but two genuine subsistent individuals (connected by the relational accident 'is kissing'). So here we are, in a sense, entitled to call 'John' and 'Mary' p a r t s of the molecule.
[2] states that X has discrete parts, where the term "parts" in this context refers again to atoms. So we should replace the content of [2] by : "X comprises more than one atom", to express the composite nature of the molecule, in which the atoms could be parts in the case of complex molecules (like "John is kissing Mary"), however, only in the sense that John and Mary are discrete subsistent individuals (connected by the Accident "is kissing" into a molecule), but just atoms in the case of simple molecules, like "Socrates-tanned", because Socrates is not a part of Socrates-tanned.
So we shall reformulate the definition of a molecule as follows :
Definition 17a
( X is a molecule ) = ( [1] X is closed under downward dependence, [2] X comprises more than one atom, [3] all atoms Y, Z which belong to X are connected, directly or indirectly, by relations of specific or generic dependence. )
In [3] we have replaced "parts of" by "belong to", because not all (types of) molecules involve parts in this respect.
So, while a molecule – being a subsistent entity -- does not have any specific or generic dependence directed outwards, it has them within.
It is possible that dependent atoms may themselves serve as carriers for further dependent accident-like entities of a higher order. For example the individual redness of my bruise is dependent on the bruise itself, which is in turn dependent on me (SMITH, 1997). Such dependencies can form longer or shorter chains, but always of finite length, because the dependence must stop somewhere. It terminates with one or more independent atoms.
Critical Comment on Definition 17 (and 17a).
When we consider the phenomenon "John is kissing Mary", we must admit that there are two genuine individuals involved. In fact we see an interaction between two independent systems, namely John and Mary. This is quite different from a simple molecule like "Socrates runs". In the latter case we have one system finding itself in a certain condition or state.
Perhaps it is better to intepret "John is kissing Mary" as John, who happens to kiss (Mary), and Mary, who happens to be kissed (by John), i.e. as two molecules, temporarily united into a higher-order molecule.
It is clear that further investigation into these matters is necessary.
ESSENTIAL PARTS
"Substances, as we have seen, may have substantials as proper parts. Accidents, correspondingly, may have accidentals as proper parts. Both substances and accidents may also, however, have essential parts, parts whose destruction leads necessarily to the destruction of the whole. Jim's individual humanity is an essential part of Jim. Hue, saturation and brightness are essential parts of the accident that is Jim's individual white or whiteness. Pitch, timbre and loudness are essential parts of Jim's present whistle."
Let us define :
Definition 18
( X is an essential part of atom Y ) = ( [1] X is an individual proper part of Y, and [2] no part of X is substantial or accidental or a boundary, and [3] Y is necessarily such that it cannot exist unless X exists. )
[1] does not allow X = Y, i.e. X is not identical to a Mereo-totality (carrier-only), nor to an Accident.
[2] implies that such an essential part, or a proper part thereof, is, again, not a Mereo-totality, nor a spatial part (like a substantial or a boundary) of such a Mereo-totality, and that it is also not an occurrent entity, and, finally, that it is not a determination of a substantial, i.e. it is not a part of an Accident. Although an essential part is a proper part of the atom, it pervades the whole atom. This should be clear from the above examples, and is compatible with the atoms being continua. SMITH continues :
"Standardly one and the same atom can be partitioned into essential parts in a variety of different ways, each one of which captures some aspect of the atom's structure. The idea is that the internal structure of every atom could be represented exhaustively by a family of distinct complex partitions, representing cuts through reality of different sorts and on different levels, in which all essential parts would be eventually displayed."
All this is not without problems.
Definition 18 intends to define what "X is an essential part of atom Y " should mean.
An atom is either a Mereo-totality (as carrier-only), or an Accident.
That an Accident has essential parts is unproblematic.
But what is atom Y when it is not an Accident? It should be precisely that what is signified by Definition 12, implying that Y does not involve inherence. It should be the carrier-only. Not a full-fledged Mereo-totality or Substance. So Y is not determined (by Accidents), it is only potentially determined. If it were actually determined, it would be a molecule, not an atom.
So how can such an atom (in this case a carrier-only) have "essential parts"? How can X be an essential part of atom Y? Is X a determination nonetheless? Yes, it is a necessary non-replaceable determination.
SMITH' example is : Jim's individual humanity is an essential part of Jim.
There "Jim" should be "atom Y ", and "Jim's individual humanity" should be " X ". So "Jim" should be the carrier-(of Accidents)-only.
But even without Accidents, Jim is still determined in some way. Jim is determined to be a human being : Jim possesses humanity.
Jim (as carrier-only), let us call it J, cannot exist, unless (his individual) humanity, let us call it H, exists. But, because J and H are not discrete ( H pervades all of J ), J is not specifically dependent on H (see Definition 3), and thus not one-sidedly specifically dependent on H, i.e. it is not a matter of inherence (See Definition 4), as was to be expected.
Let us dwell a little longer on this point.
In contrast to such an all-pervading content, as Jim's humanity (which as such is not confined to a certain part of Jim), a per accidens determination (Accident), which as such is one-sidedly specifically dependent, does not pervade the whole Totality.
When we look to some determination as it is in itself, we cannot decide whether it is, or is not, an all-pervading determination, and thus whether it is, or is not, an essential part. Only the given actual context can decide on this issue : The blue color of my bruise, although per se for such a bruise, is accidental with respect to my body (which is a true Totality). On the other hand, the blue of a crystal of copper sulfate (CuSO4 . 5H2O) is all-pervading, i.e. it is everywhere present in the crystal. It cannot be removed without destroying the essence (specific identity) of the crystal. Because 'blue' also occurs elsewhere, it is not a specific, but a per se generic proprium for a copper sulfate crystal, that is, a phenotypic per se determination of it, and as such an essential part (here we, of course mean the material configuration in the crystal that is responsible for the blue color when we look to such a crystal exposed to daylight). On the other hand, qua what it is (all by itself), 'blue' is a quality, and thus a predicament (and in a predication it can in some cases refer to an essential determination of something, in other cases to an accidental determination of something).
Definition 18 excludes accidentals, and by implication Accidents. So it is presupposed that a Mereo-totality is not only (going to be) determined by Accidents, but that there are also determinations of another nature (than Accidents) involved. These are the "essential parts". They display a dependence relation that obtains in the opposite direction : While Accidents are dependent on the carrier-only, the latter is dependent on its essential parts.
So the difference between accidental determinations (that come to determine a carrier-only) on the one hand, and the essential parts of the carrier-only, on the other, turns on a difference of dependence relations only.
Both are, however, determinations of a (full-fledged) Mereo-totality (and thus both are phenotypic).
Now it could be alternatively asserted that a full-fledged Mereo-totality is dependent on one or another complete set of determinations, i.e. a set in which all types of determinations are represented. The "one or another" means that this dependence is of a generic nature only.
Could such a complete set, that -- it is true -- changes with time, be equated with "an essential part" of the full-fledged Mereo-totality? Stated more precisely, could the here-and-now full-fledged Mereo-totality depend for its existence entirely on the here-and-now complete set of determinations, so that we can dispose of the introduction of a new kind of determination – "essential parts" -- after all?
If this would indeed be the case, we could say that any determination is dependent on the carrier-only, but (then we must also say) that the complete set of here-and-now determinations (whatever this set is here or there, now or then) is essential, not for the carrier-only, but for the very being of the full-fledged Mereo-totality, and through this for the co-existence of the carrier-only.
Let me dwell on this a little further.
In order for an observable thing to exist, a complete set of determinations, in which all types of determination (like Quantity, Quality, Relation, etc.) are represented, must be 'presupposed'. Only on completion, this set, all by itself, creates the carrier-only, i.e. this complete set IS the carrier-only, which is now equivalent to the full-fledged Mereo-totality. This Mereo-totality is indeed a totality of Accidents.
The distinction between the carrier-only and Accidents, only becomes apparent when we consider one Accident only, or when we consider an incomplete set of Accidents. Such a single Accident, or an incomplete set of Accidents, inheres in the complete set of Accidents.
But maybe this is not so.
In Part One of the Essay on Determinations ( See HERE ) I distinguish between the "phenotypic domain" and the "genotypic domain" of a Substance, and by utilizing these concepts we can speculate further :
With respect to determinations of a Mereo-totality a complete set of types is ontologically presupposed. It is a general precondition for something to be a Mereo-totality. For many determinations their being a pre-condition does not imply their ultimate specification, as long as we consider the Mereo-totality, not as a here-and-now entity, but as an entity considered over the whole time span of its individual existence, i.e. as an individual historical entity. Some of these determinations are wholly extrinsic, like the location of the Mereo-totality, and its point in time. Others need to be actualized (and thus be ultimately specified) by extrinsic agents, but only when we consider the Mereo-totality as a here-and-now entity.
But some of the determinations i n t r i n s i c a l l y must come in (their) ultimate specifications already when the Mereo-totality is considered as just an individual historical entity : As such, i.e. as completely specified, they are generated by the (particular) dynamical law (while their general type was already ontologically presupposed).
So while the complete set of types of determinations is just a general precondition for any Mereo-totality to exist, and thus is not a carrier-only or subject (see directly below), the determinations, directly and totally generated by the dynamical law are the essential parts belonging to the Mereo-totality's phenotypical domain. And such determinations turn out to be all-pervading determinations, that is, they are everywhere present in the given substantial being (The Mereo-totality should now be moreover a genuine Substance) (NOTE 3). The particular dynamical law itself is also an essential part of the (particular species of) Substance, but a part residing in the Substance's genotypical domain.
Just above we said that because the complete set of types of determinations is just a general precondition for any Mereo-totality to exist, this set is not a carrier-only. Let us explain this.
First of all, the complete set of types of determinations (accidents) is a general precondition for the fully-fledged Mereo-totality to exist. Therefore it is (also) a general precondition for the carrier-only to co-exist. But as g e n e r a l precondition (for the Totality to exist) it doesn't c a r r y anything. It doesn't carry its special over-forming, but is (only) c o n t r a c t e d to it (i.e. the 'general' is contracted, resulting in the 'special'). And thus our general precondition is not a carrier-only. We do not say : "animal est homo" (in the sense of : carries homo, like we do say "man is white", in which 'white', where this is actually the case, is carried by a human body in the form of some local material structure). Likewise we also do not say "color is red" (because the color of something can also be blue, yellow, etc.). 'Red' is not carried by 'color', but color can be contracted to 'red'.
The dynamical law is thus considered to represent the genotypical domain of the Substance in question, and is equated with the Essence of that Substance. This Essence remains the same under accidental changes during which the (complete) set of types also remains the same, but the latter is, as has been said, nevertheless not the carrier-only, not the subject, because it is only a general precondition for a Mereo-totality to exist. General-Specific is not a Carrier-Carried relation.
As has been said, some determinations appear to be necessary determinations (they persist during the whole time-span of the existence of their Substance). They are necessary representatives of the (complete) set (of types) of determinations. For example : The complete collection of actual symmetries, i.e. the total symmetry, of a crystal, which is called its Space Group, is one of the determinants for the crystal's identity. We could say : it is an essential part of the crystal ( I consider a crystal to be a genuine Substance). If this Space Group is replaced by another, then the crystal's identity is changed. So the Space Group indeed appears to be an essential part (See also the Essay on Crystals and Metaphysics ).
If we, for example, replace the Space Group R3*c (The * is normally written as a score above the preceding numeral) of the mineral Calcite (CaCO3 ) by another Space Group, say Pmcn -- under conservation of chemical composition -- then we obtain the mineral Aragonite (CaCO3 ), while a replacement of one crystal habit ( = the general shape ) of Calcite by another (say, a transition from prismatic to scalenohedral) is not supposed to give rise to another mineral species, i.e. the crystals remain calcite crystals.
Or, when we see a (profound) change in the chemical composition when we go from one crystal to another having the same symmetry (the same Space group), we assume that we have to do with disparate substances (in the metaphysical sense) differing qua whatness, despite their identical symmetries.
From this it should be clear (but see below) that the distinction between necessary determinations on the one hand, and just occurrent determinations (Accidents) on the other, seems more or less arbitrary, for it seems merely stipulated (and not shown) that the Space Group belongs to the co-determinants of a crystal's specific identity. But why not its habit (instead)?
Further, it is possible that atomic or ionic constituents (atoms, in a chemical sense, or electrically charged atoms) of a crystal are being replaced (substituted) by other (specifically different) constituents of approximately the same size. By stipulation the crystal then changes identity (except when we enter the possibility of certain substitutions of atomic species into the definition of chemical composition), because chemical composition is stipulated (and not demonstrated) to be a co-determinant of the crystal's specific identity, even though (as in this case) the (conceptual or real) transition does not involve any space-time discontinuity : it still appears to be the same individual.
So the "essential parts" seem to be of a more or less arbitrary nature.
Because in Metaphysics (when conceived as a general ontology) one often sticks to the same example, namely the human individual, say, Socrates, things appear to be all together too clear and easy : Socrates undergoes a brain damage, which changes his psychological character, but still remains Socrates .... or does he? That is just a matter of stipulation.
The dynamical systems approach on the other hand (developed on this Website), solves this problem, by recognizing the fact that every intrinsic whole is generated by one dynamical system, governed by one dynamical law. This law can be identified with the Essence or Identity of such a whole, and can be considered to be the very essential part of that whole, residing in its genotypical domain. In the case of crystals the Space Group + Chemical Composition are then direct effects of such a law, and so are also essential parts, but residing in the phenotypical domain. In this there is no stipulation involved. The only assumption made is that an intrinsic whole is generated (or admits to be considered as such) by ONE dynamical system (involving ONE dynamical law). If there is a multitude of dynamical systems involved in this generation, I assume that these systems are coordinated in some way so as to constitute in fact ONE dynamical system after all. Where this is not the case, i.e. where such an assumption cannot be made, we have to do with an aggregate.
Of course it could be the case that all dynamical systems in the Universe are coupled and interdependent, implying that there is in fact only ONE dynamical system in the Universe, namely the Universe itself. We then come closer, in a way, to some eastern philosophies, that do not admit of any discreteness of objects, and also not of any fundamental distinction between subject and object. In this case a Substance-Accident Metaphysics becomes untenable.
But for the time being I cling to the approach which presupposes the existence of discrete intrinsic things (wholes), each generated (or interpretable as (so)generated) by ONE dynamical system. And wherever a local multitude of dynamical systems, which are not mutually coupled, is involved, we have to do with an aggregate.
As remarked earlier, sometimes one and the same single dynamical system generates not one product, but a multitude of it. The original elements of the dynamical system are, as it seems, not organized into one structured more or less continuous whole, but are scattered and dipersed in a stronger or weaker degree. Should the result of such a dynamical system be interpreted as one single entity or being, on the basis of the fact that it is produced by one single dynamical system, despite the fact that this supposedly single entity seems to be more of a multitude of more or less mutually independent and separate entities? Or should that result be interpreted as just an aggregate? Here it is indeed that dynamical systems theory is of no further help anymore. And it is here that our ontological investigation will benefit most of Mereotopology.
The science of Mereotopology directly investigates the product, not its history. It evaluates the internal coherence of parts in such a product, in order to determine whether we have to do with a single thing or a multitude of it.
I hope this discussion (which cannot, for the time being, be finally concluded and settled) stimulates further pondering about the Essence of a Substance, and its accidental determinations.
UNIVERSALS
SMITH, 1997, focuses on universals insofar as they are common natures, and not insofar as they figure as terms in predications. In this latter case we are indeed doing Logic, not Metaphysics. But it is still the question whether 'common natures' can really exist in extra-mental reality as common natures. Indeed, as common nature it exists only in the mind. It is a sign, term, or concept, referring to many individuals in extra-mental reality.
An example of a universal is man. And this can be instantiated in Socrates, but also in Plato, etc. So the universal term "man" refers to something in Reality, that is present in some individuals. In what way it is supposed to be present in them is not completely clear, and is being disputed for a long time.
The universal is a one-in-many-things. It is not spread out in a physical sense among the things which instantiate it, because then those things would be physically one. It is real already in one object (SMITH). It cannot however be itself a being, a thing, because it can be present in several discrete things at once. So it cannot be a concrete part.
Of course it could be that every universal is only a fiat delineation, i.e. a delineation made by the investigating mind, and not intrinsic to the relevant things. But Natural Science uses such universals, and she has showed to be able to do correct predictions, i.e. predictions that came true. But this would, however, still occur when the commonness in question was based on very close similarity, but not complete identity. For example Natural Science presupposes that Iron has a common nature, meaning that every individual case of Iron (i.e. every individual piece of Iron) will behave precisely in the same way under the same conditions. But Science can never do measurements in absolutely precise ways : a slightly varying nature in the corresponding pieces of Iron would not be detected, but even then, to do Natural Science is still possible. I have discussed this state of affairs in the beginning of the Essay on Categories (In the Non-classical Series), and, more extensively, in the Essay on The Species-Individuum Structure (In the Critical Series).
According to SMITH the dependence of a universal is a dependence on that in which it is instantiated. This "that" is not one particular thing, but a possible many (of them), in a disjunctive way. If Socrates is not available to serve as host for the universal MAN, then Plato or Peter will do just as well. It is (SMITH) a case of generic dependence.
There are several sorts of generic dependence. For example I need oxygen molecules in order to be able to live, but I am not dependent on specific oxygen molecules, for example on these ones here, or on those ones out there. This is a generic dependence of one Substance on other Substances (each oxygen molecule can be considered a Substance). In addition this is a causal dependence. Other sorts of generic dependence can be formal (like the example cited by SMITH was one), namely the generic dependence of a Substance on Accidents (because as carrier-only it cannot exist). These Accidents need not be specific ones. Socrates need not be white, but he must have some color.
We saw earlier that an individual Accident is specifically dependent on its Substance. We can call this specific inherence. Correspondingly we can call the generic dependence of a universal on that in which it is instantiated a generic inherence.
The specific dependence of Accidents refers to the dependence of, say, this redness. And This redness depends on a certain particular individual Substance to which we can point with the finger. But as soon as we conceptually isolate an Accident, and this is what we do when we speak of "this redness", without any emphasis on "this", then "this redness" turns into "redness", i.e. it turns into a universal. And as a universal it is generically dependent on some individual, not specifically. So it is not completely clear whether Accidents are generically or specifically dependent on some individual.
For the time being we could assume however, that when we speak of "this redness" we do not in fact isolate it (so we do not transform it into a universal) : we also refer, be it implicitly, to its particular carrier, that's why we said "this redness". And then "this redness" is specifically dependent on that carrier. When we speak, on the other hand, of "redness", then we are isolating it as "redness", i.e. we turn "this redness", which we had implicitly in mind, into a universal. So "this redness" is then specifically dependent, while "redness" is generically dependent, and as such a universal.
Clearly, the Accident "this redness" is ontologically equivalent to the Accident "my headache" we spoke about earlier. Both are individual Accidents, and "this redness" also refers to a particular individual carrier.
To refer to a carrier should certainly count as an intrinsic feature of any Accident.
But to refer to a particular individual carrier is no doubt an extrinsic feature of any Accident as such (Of course it is an intrinsic feature of any individual Accident).
Definition 19 (focused on universals)
( X is generically dependent on Y ) = ( [1] Y is an individual, [2] X is part of Y, [3] X is necessarily such that either Y exists or there exists some Z discrete from Y containing X as part. )
We can then define :
Definition 20
( X is a universal ) = ( X is generically dependent on some Y )
[2] of Definition 19 states that X is part of Y. But it is clear that it cannot be a concrete material part of Y, insofar as it is considered as a universal. We can however imagine that a universal is represented by something concrete, i.e. by a relevant concrete part of some individual thing, and that it can also be so represented by corresponding parts of other things. But then the universal is no more than a sign, pointing to many such parts, wherever they may be, at once, and thus no more than a universal term. So what is present in the thing, as a fundament of universality, can itself never be a genuine universal, because it is particular. So the 'universal' nature, for example the common nature of Iron, is some individual pattern that is repeatable, and such natures are the fundaments of natural laws. So only the term is universal, namely in its function of signifying many things univocally.
[3] of definition 19 means that X can be instantiated in Y, but also in Z.
X does not necessarily relate to one particular individual only.
Comment on Definition 19.
"X is generically dependent on Y" presupposes that Y exists. But "generically" means that X is not exclusively dependent on Y. If Y does not happen to exist, X is dependent on some one Z, which would be discrete from Y, were Y existing.
This concludes our exposition of a Mereotopology of Reality (mainly based on SMITH, 1997).